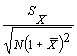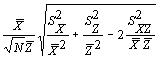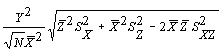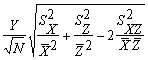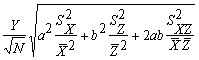|
ФЕДЕРАЛЬНОЕ АГЕНТСТВО |
||
|
|
РЕКОМЕНДАЦИИ |
Р 50.1.062- |
Статистические методы
НЕОПРЕДЕЛЕННОСТЬ ПРИ ПОВТОРНЫХ ИЗМЕРЕНИЯХ И ИЕРАРХИЧЕСКИХ ЭКСПЕРИМЕНТАХ
|
|
Москва Стандартинформ 2008 |
Предисловие
Цели и принципы стандартизации в Российской Федерации установлены Федеральным законом
от 27 декабря
Сведения о рекомендациях
1 ПОДГОТОВЛЕНЫ Открытым акционерным обществом «Научно-исследовательский центр контроля и диагностики технических систем» (ОАО «НИЦ КД») на основе собственного аутентичного перевода международных технических условий, указанных в пункте 4
2 ВНЕСЕНЫ Техническим комитетом по стандартизации ТК 125 «Статистические методы в управлении качеством продукции»
3
УТВЕРЖДЕНЫ И ВВЕДЕНЫ В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 27 декабря
4 Настоящие рекомендации являются идентичными международным техническим условиям ИСО/ТУ 21749:2005 «Неопределенность измерений для использования в метрологии. Повторные измерения и иерархические эксперименты» (ISO/TS 21749:2005 «Measurement uncertainty for metrological applications - Repeated measurements and nested experiments»).
Наименование настоящих рекомендаций изменено относительно наименования указанных международных технических условий для приведения в соответствие с ГОСТ Р 1.5-2004 (подраздел 3.5).
При применении настоящих рекомендаций рекомендуется использовать вместо ссылочных международных стандартов соответствующие им национальные стандарты Российской Федерации, сведения о которых приведены в дополнительном приложении В
5 ВВЕДЕНЫ ВПЕРВЫЕ
Информация о введении в действие (прекращении действия) настоящих рекомендаций, изменениях и поправках к ним, а также тексты изменений и поправок публикуются в информационном указателе «Национальные стандарты»
Содержание
Введение
Испытательные, калибровочные и другие лаборатории обычно должны представлять результаты измерений с соответствующей неопределенностью. Оценка неопределенности - непрерывный процесс, требующий затрат времени и средств. В частности, многие испытания и другие процедуры, проводимые в лаборатории, имеют два или три источника неопределенности. В соответствии с Руководством по выражению неопределенности измерений (ИСО/МЭК Руководство 98:1995 [1], далее - GUM1)) настоящие рекомендации концентрируют внимание на использовании дисперсионного анализа (ANOVA2)) для оценки отдельных составляющих неопределенности, в основном типа А, с использованием статистических методов.
Разработанный лабораторией план эксперимента должен предусматривать выполнение требуемого количества измерений, анализ результатов которых обеспечит определение составляющих неопределенности. При планировании, выполнении, последующем анализе результатов эксперимента и оценке неопределенности необходимо знание методов анализа данных, в частности статистического анализа. Поэтому для персонала лаборатории важно иметь необходимые ресурсы для планирования, сбора и анализа данных.
В настоящих рекомендациях предполагается, что оценки составляющих неопределенности (оценки типа А) могут быть получены на основе статистического анализа повторных измерений с помощью соответствующих приборов, объектов испытаний, оборудования или выбранных образцов.
Настоящие рекомендации содержат рекомендации по оценке неопределенности, связанной с измерением характеристик объектов испытаний, например при контроле непрерывного производства. Такая неопределенность объединяет вклады в неопределенность процесса измерений и изменчивости производственного процесса. Оба типа вкладов включают в себя составляющие, зависящие от работы операторов, внешних условий и других воздействий. В целях разделения влияния процесса измерений и изменчивости, свойственной производственному процессу, проводят измерения на выбранных образцах для получения данных непосредственно о процессе измерений. Такие измерения обычно идентичны выполненным на объектах испытаний. В частности, измерения на выбранных образцах используют для идентификации зависящих от времени воздействий, чтобы эти воздействия можно было оценить и сопоставить с базой данных результатов измерений на выбранных образцах. Выбранные образцы также полезно использовать для контроля смещения и долгосрочного дрейфа процесса, если исходный уровень измеряемых величин установлен по предыдущим данным.
В разделе 4 кратко описаны статистические методы оценки неопределенности в соответствии с принципом, рекомендованным в [1], указаны требования к выбранным образцам, описаны этапы оценки неопределенности и приведены примеры. В разделе 5 рассмотрены оценки типа А. Иерархические эксперименты в ANOVA используют в случае зависящих от времени источников неопределенности. Рассмотрены также другие источники неопределенности, такие как конфигурация измерений, неоднородность материала, смещения, связанные с конфигурацией измерений, и соответствующий анализ неопределенности. Оценка неопределенности типа В (не использующая статистические методы) рассмотрена в разделе 6. Широко использован закон распространения неопределенности, описанный в [1]. В разделе 7 приведены формулы, полученные путем применения этого закона к некоторым функциям одной и двух переменных. В разделе 8 в качестве примера рассмотрена оценка неопределенности типа А при исследовании прибора, когда составляющие неопределенности получены из различных источников. В приложении А приведен список символов, используемых в настоящих рекомендациях.
Обозначения, использованные в настоящих рекомендациях, несколько отличаются от обозначений, принятых в стандартах серии ИСО 5725 и ИСО/ТУ 217483). Различия в обозначениях указаны в таблице.
Таблица
|
Условия получения результатов измерений |
Обозначения, принятые |
|
|
в настоящих рекомендациях |
в ИСО 5725 и ИСО/ТУ 21748 |
|
|
Условия повторяемости |
σ |
σr |
|
Разные дни |
σD |
σI(T) |
|
Разные серии |
σR |
σI(TO) |
|
Разные лаборатории |
- |
σR |
В настоящих рекомендациях широко использованы термины, относящиеся к планированию эксперимента и конфигурации.
В соответствии с ИСО 3534-34)
иерархический эксперимент (nested design): Эксперимент, в плане которого каждый уровень данного фактора появляется только с одним уровнем другого фактора.
Применительно к настоящим рекомендациям и в соответствии с ИСО 100075)
конфигурация процесса измерений (measurement process configuration): Способ применения процесса измерений, характеризуемый взаимосвязанными функциональными и техническими показателями, соответствующими требованиям к конструкции, изготовлению, эксплуатации и обслуживанию использованного измерительного оборудования и средств измерений.
1) GUM - ISO/IEC Guide 98:1995 Guide to the expression of uncertainty in measurement.
2) ANOVA - Analysis of variance.
3) ИСО 5725-1:1994 Точность (правильность и прецизионность) методов и результатов измерений. Часть 1. Основные положения и определения.
ИСО 5725-2:1994 Точность (правильность и прецизионность) методов и результатов измерений. Часть 2. Основной метод определения повторяемости и воспроизводимости стандартного метода измерений.
ИСО 5725-3:1994 Точность (правильность и прецизионность) методов и результатов измерений. Часть 3. Промежуточные показатели прецизионности стандартного метода измерений.
ИСО 5725-4:1994 Точность (правильность и прецизионность) методов и результатов измерений. Часть 4. Основные методы определения правильности стандартного метода измерений.
ИСО 5725-5:1998 Точность (правильность и прецизионность) методов и результатов измерений. Часть 5. Альтернативные методы определения прецизионности стандартного метода измерений.
ИСО 5725-6:1994 Точность (правильность и прецизионность) методов и результатов измерений. Часть 6. Использование значений точности на практике.
ИСО/ТУ 21748:2004 Руководство по использованию оценок повторяемости, воспроизводимости и правильности при оценке неопределенности измерений.
4) ИСО 3534-3:1999 Статистика. Словарь и условные обозначения. Планирование экспериментов.
5) ИСО 10007:2007 Системы менеджмента качества. Руководящие указания по управлению конфигурацией.
РЕКОМЕНДАЦИИ ПО СТАНДАРТИЗАЦИИ
|
Статистические методы НЕОПРЕДЕЛЕННОСТЬ ПРИ ПОВТОРНЫХ ИЗМЕРЕНИЯХ И ИЕРАРХИЧЕСКИХ ЭКСПЕРИМЕНТАХ Statistical methods. Uncertainty for repeated measurements and nested experiments |
Дата введения - 2008-09-01
1 Область применения
Настоящие рекомендации устанавливают основную структуру оценки и методы объединения составляющих неопределенности в соответствии с GUM [1], а также статистические методы, использующие дисперсионный анализ (ANOVA), для оценки (обычно статистической) отдельных составляющих неопределенности. Для полноты включено краткое описание оценки неопределенности типа В (нестатистической).
В настоящих рекомендациях рассмотрены ситуации, когда составляющие неопределенности могут быть оценены на основе статистического анализа повторных измерений, выполненных с применением нескольких средств измерений (приборов) на объектах испытаний или выбранных образцах.
Настоящие рекомендации устанавливают методы оценки неопределенности по иерархическим двух- и трехуровневым экспериментам. Более сложные планы эксперимента, когда, например, имеется связь между воздействиями оператора и прибора (взаимное влияние), не рассмотрены.
Рекомендации не применимы к измерениям, которые не могут быть повторены, таким как разрушающие измерения или измерения на динамически меняющихся системах (поток жидкости, потоки электронов или телекоммуникационные системы). Рекомендации не предназначены для сертификации образцов сравнения (особенно для химических веществ) и для калибровки, когда результаты измерений сравнивают, используя схему «взвешенного эксперимента». Для сертификации образцов сравнения см. ИСО Руководство 35.
При использовании результатов межлабораторных исследований необходимо применять методы, представленные в ИСО/ТУ 21748. Главное различие между ИСО/ТУ 21748 и настоящими рекомендациями состоит в том, что в ИСО/ТУ 21748 рассмотрены данные воспроизводимости (с неизбежным влиянием повторяемости), тогда как в настоящих рекомендациях рассмотрены данные повторяемости и использование дисперсионного анализа для их обработки.
Настоящие рекомендации применимы к измерениям различных видов, например к измерениям длины, угловых параметров, напряжения, сопротивления, массы, удельного веса и т.п.
2 Нормативные ссылки
В настоящих рекомендациях использованы нормативные ссылки на следующие стандарты:
ИСО 3534-1:2006 Статистика. Словарь и условные обозначения. Часть 1. Общие статистические термины и термины, используемые в вероятностных задачах
ИСО 3534-3:1999 Статистика. Словарь и условные обозначения. Часть 3. Планирование экспериментов
ИСО 5725-1:1994 Точность (правильность и прецизионность) методов и результатов измерений. Часть 1. Основные положения и определения
ИСО 5725-2:1994 Точность (правильность и прецизионность) методов и результатов измерений. Часть 2. Основной метод определения повторяемости и воспроизводимости стандартного метода измерений
ИСО 5725-3:1994 Точность (правильность и прецизионность) методов и результатов измерений. Часть 3. Промежуточные показатели прецизионности стандартного метода измерений
ИСО 5725-4:1994 Точность (правильность и прецизионность) методов и результатов измерений. Часть 4. Основные методы определения правильности стандартного метода измерений
ИСО 5725-5:1998 Точность (правильность и прецизионность) методов и результатов измерений. Часть 5. Альтернативные методы определения прецизионности стандартного метода измерений
ИСО 5725-6:1994 Точность (правильность и прецизионность) методов и результатов измерений. Часть 6. Использование значений точности на практике
ИСО/ТУ 21748:2004 Руководство по использованию оценок повторяемости, воспроизводимости и правильности при оценке неопределенности измерений
ИСО Руководство 35:2000 Стандартные образцы. Общие и статистические принципы аттестации
3 Термины и определения
В настоящих рекомендациях применены термины по ИСО 3534-1, ИСО 3534-3, ИСО 5725 (все части).
3.1 измеряемая величина (measurand): Физическая величина, подлежащая измерению и характеризуемая единственным значением.
3.2 неопределенность измерения (uncertainty of measurement): Параметр (или оценка параметра), связанный с результатом измерений и характеризующий рассеяние значений, которые могут быть обоснованно приписаны измеряемой величине.
3.3 оценка типа A (type A evaluation): Оценка неопределенности, полученная с использованием статистических методов.
3.4 оценка типа В (type В evaluation): Оценка неопределенности, полученная без использования статистических методов.
3.5 стандартная неопределенность (standard uncertainty): Неопределенность результата измерений, представляемая в виде стандартного отклонения для одной составляющей неопределенности.
3.6 суммарная стандартная неопределенность (combined standard uncertainty): Стандартное отклонение результата конкретного измерения или серии измерений, которое учитывает одну или более составляющую неопределенности.
3.7 расширенная неопределенность (expanded uncertainty): Суммарная стандартная неопределенность, умноженная на коэффициент охвата, который обычно соответствует критическому значению t-распределения для числа степеней свободы суммарной стандартной неопределенности и вероятности, характеризующей желаемый уровень охвата.
3.8 эффективное число степеней свободы (effective degrees of freedom): Число степеней свободы стандартного отклонения, состоящего из двух или более составляющих дисперсии.
Примечание - Эффективное число степеней свободы может быть вычислено с использованием приближения Велча-Саттервейта (см. [1], пункт G.4).
3.9 иерархический эксперимент (nested design): Эксперимент, в соответствии с планом которого каждый уровень (т.е. каждое возможное значение) данного фактора появляется только с одним уровнем любого другого фактора.
Примечания
1 Адаптированное определение из ИСО 3534-3.
2 Уровень - термин 1.6 по ИСО 3534-3.
3.10 фиксированное воздействие (fixed effects): Воздействие, являющееся результатом предварительного выбора уровней каждого фактора из области значений фактора.
3.11 воздействие случайности (random effects): Воздействие, являющееся результатом случайного отбора на каждом уровне каждого фактора из совокупности уровней каждого фактора.
3.12 сбалансированный иерархический эксперимент (balanced nested design): Иерархический эксперимент, в котором количество уровней факторов на каждом уровне иерархии одинаково.
[ИСО 3534-3:1999]
3.13 средний квадрат случайных ошибок (mean square for random errors): Сумма квадратов ошибок, деленная на соответствующее число степеней свободы.
Примечание - Число степеней свободы - термин 2.54 по ИСО 3534-1.
4 Статистические методы оценки неопределенности
4.1 Подход к оценке неопределенности по GUM
GUM [1] рекомендует корректировать результат измерений относительно всех признанных значимыми систематических воздействий, так чтобы результат представлял собой наилучшую (или, по крайней мере, несмещенную) оценку измеряемой величины и можно было построить полную модель измерительной системы. Модель устанавливает функциональную связь между набором входных величин, от которых зависит измеряемая величина, и измеряемой величиной (выходной величиной). Цель оценки неопределенности состоит в нахождении интервала, который в среднем охватывает большую часть значений, приписываемых измеряемой величине. Поскольку смещение невозможно определить точно, если результат измерений скорректирован на смещение, корректировке также соответствует неопределенность.
Общий подход к оценке неопределенности, начиная с процесса моделирования, является следующим:
Примечание - В основе указанного подхода лежит предположение о взаимной независимости входных величин. Возможно обобщение для зависимых входных величин (см. [1], пункт 5.2).
a) Разрабатывают математическую модель (функцию) процесса измерений или измерительной системы, которая связывает входные величины, включая воздействующие величины, с выходной величиной (измеряемой величиной). Во многих случаях эту модель можно описать формулой (или формулами), которую используют для вычисления результата измерений с учетом, при необходимости, случайных воздействий, воздействий внешних условий и других, таких как корректировка смещения, которая может повлиять на результат измерений.
b) Определяют наилучшую оценку и соответствующую стандартную неопределенность (неопределенность, выражаемую через стандартное отклонение) для функции, описывающей модель измерительной системы.
c) Оценивают вклад каждой входной величины в стандартную неопределенность результата измерений. Эти вклады должны учитывать неопределенность, соответствующую случайным и систематическим воздействиям входных величин, и могут предусматривать более детальные оценки неопределенности.
d) Объединяют стандартные неопределенности для получения суммарной стандартной неопределенности результата измерений. Эту оценку неопределенности выполняют в соответствии с [1], используя закон распространения неопределенности или общие аналитические или численные методы, если условия для закона распространения неопределенности не выполняются или отсутствует необходимая информация.
e) При необходимости стандартную неопределенность результата измерений умножают на коэффициент охвата для вычисления расширенной неопределенности и, таким образом, получают интервал, который накрывает значения измеряемой величины с заданным уровнем доверия. В GUM [1] установлен способ вычисления коэффициента охвата. Если число степеней свободы всех входных величин равно бесконечности, коэффициент охвата определяют с помощью нормального распределения. В противном случае число степеней свободы для суммарной стандартной неопределенности оценивают на основе степеней свободы стандартной неопределенности, соответствующей наилучшим оценкам входных величин, используя формулу Велча-Саттервейтта.
В соответствии с [1] оценку стандартной неопределенности можно определять любыми методами. Существует различие между оценкой неопределенности типа А, полученной на основе повторных наблюдений, и оценкой неопределенности типа В, полученной любыми другими способами. В оценке суммарной стандартной неопределенности оба типа оценок должны быть представлены дисперсиями (квадрат стандартной неопределенности) и использованы одинаковым образом.
Все детали этой процедуры и дополнительные предположения, на которых она основана, приведены в [1].
Цель настоящих рекомендаций состоит в представлении дополнительного руководства по оценке неопределенности статистическими методами в условиях, соответствующих перечислению b), при повторении измерений входных величин или всей процедуры измерений.
В настоящих рекомендациях термин «объект» часто используется в связи с измерениями, поскольку измерение может относиться к сыпучим материалам, химическим веществам и т.д.
4.2 Выбранный образец
Выбранный образец должен:
a) быть доступен для периодических измерений;
b) быть близок по материалу и геометрии к исследуемому объекту;
c) обладать стабильностью;
d) быть всегда доступен для измерений.
Для удовлетворения указанным требованиям идеальный выбранный образец должен быть объектом, отобранным случайным образом из предназначенных для этого единиц продукции. Примеры использования выбранного образца следующие:
- при измерениях на стабильном объекте;
- при различиях между значениями двух исходных эталонов, оцененных в процессе эксперимента по калибровке.
Методы анализа измерений выбранного образца рассмотрены в 5.2.3.
В настоящих рекомендациях термин «выбранный образец» дан в общей интерпретации, что позволяет применять его к сыпучим материалам или к химическим веществам.
4.3 Этапы оценки неопределенности
4.3.1 Первым этапом оценки неопределенности является определение измеряемой величины, результат измерений которой необходимо фиксировать при испытаниях объекта. Следует обеспечить однозначное определение измеряемой величины, поскольку от этого зависит оценка неопределенности. Для этого необходимо установить, что является объектом измерений:
- величина в конкретный момент времени в конкретной точке пространства;
- величина в конкретный момент времени, усредненная по заданной пространственной области;
- величина в конкретной точке пространства, усредненная по периоду времени.
Например, характеристики твердости образца керамического материала могут сильно различаться, если они основаны:
a) на результатах измерений в указанной точке образца;
b) на среднем арифметическом по нескольким точкам образца.
4.3.2 Если значение измеряемой величины может быть измерено непосредственно, оценка стандартной неопределенности зависит от количества повторных измерений, внешних условий и эксплуатационных режимов, в которых проведены повторения. Она также зависит от других источников неопределенности, которые невозможно наблюдать в условиях повторения измерений, например от неопределенности калибровки для исходных эталонов. С другой стороны, если значение измеряемой величины не может быть измерено непосредственно, а должно быть вычислено по результатам измерений косвенных величин, должна быть определена модель (или функция), связывающая эти величины. Для оценки стандартной неопределенности измеряемой величины необходимо определить стандартную неопределенность, соответствующую наилучшим оценкам косвенных величин.
Можно выделить следующие этапы оценки неопределенности:
a) Для оценки типа А:
1) если выходная величина представлена Y, а измерения Y могут быть повторены, используют модель ANOVA для оценки составляющих дисперсий, соответствующих случайным воздействиям на Y:
- результатов повторений измерений на объекте испытаний,
- результатов измерений на выбранном образце,
- результатов измерений, выполненных в соответствии с планом эксперимента;
2) если измерения Y не могут быть непосредственно повторены и модель Y = f (X1, X2, ..., Хn) известна, а измерения входных величин Xi могут быть повторены, оценивают неопределенности, соответствующие наилучшим оценкам хi для Xi, а затем применяют закон распространения неопределенности;
3) если измерения Y или Xi не могут быть повторены, применяют оценки типа В.
b) Для оценки типа В оценивают стандартную неопределенность, соответствующую наилучшей оценке каждой входной величины.
c) Объединяют стандартные неопределенности типов А и В для получения стандартной неопределенности результатов измерений.
d) Вычисляют расширенную неопределенность.
4.4 Примеры, приведенные в настоящих рекомендациях
Целью примеров, приведенных в различных разделах настоящих рекомендаций, и более детального исследования, рассмотренного в разделе 8, является демонстрация методов оценки неопределенности, соответствующих процессам измерений, имеющим несколько источников неопределенности. Пользователь должен самостоятельно обобщить принципы, изложенные в настоящих рекомендациях. В примерах рассмотрены последствия случайных и систематических воздействий в форме смещения результатов измерений. Имеются особенности при определении значения неопределенности, наблюдаемой во времени, например неопределенности, соответствующей коротким временным интервалам (условия повторяемости), называемой краткосрочной, и неопределенности для оценки промежуточной прецизионности, характеризующей изменчивость по дням или от серии к серии (условия воспроизводимости). Пользователь должен определить интервалы времени, подходящие для рассматриваемого процесса измерений.
Для иллюстрации стратегии при работе с несколькими источниками неопределенности использованы данные Национального института стандартов и технологии (NIST) США. Рассматриваемые измерения- это измерения удельного объемного сопротивления (в Ом·см) кремниевых пластин. Измеряемая величина определена методом испытаний ASTM1).
1) ASTM - American Society for Testing and Materials (Американское общество по исследованию материалов).
Цель эксперимента состоит в оценке неопределенности удельного сопротивления кремниевых пластин на различных уровнях удельного сопротивления (Ом·см), которые были сертифицированы с использованием четырехточечного зонда определенной конфигурации. Метод испытаний - метод F84 ASTM. Удельное сопротивление, которое фиксируют для каждой пластины, - это среднее арифметическое результатов шести повторных измерений, выполненных в центре пластины за короткий отрезок времени.
5 Оценка неопределенности типа А
5.1 Общие положения
5.1.1 В общем случае любое наблюдение, которое может быть повторено (см. GUM, пункты 3.1.4 - 3.1.6), может обеспечить данные для оценки типа А. Оценки типа А могут быть получены на основе следующих данных:
- повторяемые измерения на объекте испытаний, выполняемые в процессе измерений или в дополнение к измерениям, необходимым для определения результата;
- измерения, выполненные на соответствующем объекте испытаний при валидации метода до выполнения измерений;
- измерения на выбранном образце, т.е. объекте испытаний, которые многократно выполняют (в условиях повторяемости) в ходе мониторинга стабильности процесса измерений;
- измерения на стандартных образцах или исходных эталонах;
- повторные наблюдения или определение влияния величин (например, регулярный или случайный мониторинг внешних условий в лаборатории или повторные измерения величин, используемых для вычисления результатов измерений).
5.1.2 Оценки типа А могут быть применены и к случайным, и систематическим воздействиям ([1], пункт 3.2). Единственное требование при определении оценки типа А состоит в том, что оценка компонентов неопределенности должна быть основана на статистическом анализе серии наблюдений. Особенности влияния случайных и систематических воздействий состоят в следующем:
- случайные воздействия изменяются от наблюдения к наблюдению и не могут быть устранены;
- систематические воздействия могут быть рассмотрены как постоянные для наблюдений в течение короткого периода времени и могут теоретически быть компенсированы или устранены.
Иногда трудно отличить систематическое воздействие от случайного. Это является результатом интерпретации и требует использования статистических моделей. В общем случае невозможно разделить случайные и систематические воздействия.
GUM [1] рекомендует корректировать все систематические воздействия. В этом случае остается только неопределенность случайных воздействий. Роль времени в оценке неопределенности типа А с использованием иерархического эксперимента рассмотрена в 5.2. Неопределенность, связанная с конфигурацией измерений и неоднородностью материала, рассмотрена, соответственно, в 5.3 и 5.4. Рекомендации по оценке и корректировке смещения, связанного с конфигурацией измерений, и соответствующая оценка неопределенности приведены в 5.5. От характера воздействия источника неопределенности на полученное значение зависит способ описания этого воздействия (воздействие считают случайным или систематическим) и оценки неопределенности.
В лаборатории с несколькими средствами измерений определенного типа, являющимися представителями набора всех средств измерений данного типа, различия между средствами измерений этого набора можно считать случайными, если заявленная неопределенность относится к результатам любого средства измерений, выбранного наугад из этого набора.
Наоборот, если заявленная неопределенность относится к одному (или нескольким) конкретным средствам измерений, систематическое влияние этого средства измерений по отношению ко всему набору является составляющей исследуемой неопределенности.
5.2 Роль времени в оценке неопределенности типа А
5.2.1 Зависящие от времени источники неопределенности и выбор временных интервалов
Многие случайные воздействия, зависящие от времени, часто являются результатом изменений внешних условий. Рассматриваются три уровня зависящих от времени изменений:
a) краткосрочные изменения (повторяемость или прецизионность средств измерений);
b) промежуточные изменения (изменения, соответствующие дням или операторам или оборудованию, называемые промежуточной прецизионностью);
c) долгосрочные изменения (изменения, соответствующие сериям, или стабильность, которая может не относиться ко всем процессам, или условия промежуточной прецизионности).
Приведенное описание необходимо пользователю для определения интервалов времени, на которых основан процесс измерений (минуты, часы или дни).
Одной из причин такого подхода является то, что большинство современных средств измерений обладают высокой повторяемостью и прецизионностью измерений на коротких отрезках времени. В течение длительного периода времени доминирующими источниками неопределенности для процесса измерений могут быть изменения окружающей среды. Заявленное значение неопределенности может не соответствовать действительности, если оно относится к результатам измерений, которые не могут быть воспроизведены в течение продолжительного времени. Потребитель имеет право знать неопределенность, соответствующую результатам измерений, независимо от времени выполнения измерений.
Для описания многих процессов измерений и оценки составляющих неопределенности, зависящих от времени, обычно достаточно эксперимента с двумя уровнями (двухуровневого эксперимента). Для новых процессов измерений или процессов, характеристики которых недостаточно понятны, может потребоваться три уровня. Эксперимент с тремя уровнями рассматривают как специальный случай двухуровневого иерархического эксперимента.
Иерархические эксперименты, имеющие более трех уровней, в настоящих рекомендациях не рассмотрены. Однако описанные подходы могут быть на них распространены (см. ИСО 5725-3).
5.2.2 Трехуровневый эксперимент
5.2.2.1 Эксперимент с тремя уровнями рекомендуется для исследования влияния источников изменчивости, проявляющихся в течение продолжительного времени. Во многих случаях нет необходимости в оценке взаимного влияния воздействий, зависящих от времени. Иерархические эксперименты могут быть выполнены на нескольких уровнях. Для измерительных систем, у которых источники неопределенности результатов измерений недостаточно понятны и предварительно не были исследованы, рекомендуется использовать трехуровневый эксперимент.
На основе анализа многих измерительных систем могут быть рекомендованы следующие уровни, которые при необходимости должны быть адаптированы к конкретной ситуации:
a) уровень 1 - измерения, выполняемые за короткий промежуток времени для учета повторяемости измерений;
b) уровень 2 - измерения, выполняемые в течение дней (или других соответствующих интервалов времени);
c) уровень 3 - измерения, выполняемые в течение серий, установленных по месяцам.
Обозначения, относящиеся к этим уровням:
- уровень 1: J (J > 1) - повторения;
- уровень 2: К (К > 1) - дни;
- уровень 3: L (L > 1) - серии.
Для сбора данных рекомендуется следующий сбалансированный трехуровневый иерархический эксперимент. Он описывает долгосрочные изменения в процессе измерений:
Ylkj = μ + γl + δlk + εlkj.
Здесь Ylkj (l = 1,..., L; k = 1,..., K; j = 1,..., J) представляет измерение для j-го повторения в k-й день
l-й серии. Члены уравнения, описывающего модель, характеризуют случайные воздействия на процесс измерений, которые меняются в зависимости от серии, дня и краткосрочного интервала времени. Цель эксперимента состоит в том, чтобы оценить составляющие дисперсии, соответствующие источникам изменчивости. Пусть составляющими дисперсии, соответствующими дню и серии (δ и γ) являются ![]() и
и ![]() , а составляющей дисперсии, соответствующей погрешности измерений (ε), является σ2. Эти составляющие дисперсии формируют основу стандартной неопределенности.
, а составляющей дисперсии, соответствующей погрешности измерений (ε), является σ2. Эти составляющие дисперсии формируют основу стандартной неопределенности.
Таблица 1 - Таблица ANOVA для трехуровневого иерархического эксперимента
|
Источник |
Число степеней свободы v |
Сумма квадратов отклонений SS |
Средний квадрат отклонений MS |
Математическое ожидание среднего квадрата отклонений |
|
Серия |
L - 1 |
SSR |
MSR |
σ2 + J |
|
День |
L (К - 1) |
SSD(R) |
MSD(R) |
σ2 + J |
|
Случайная ошибка |
LK(J - 1) |
SSE |
MSE |
σ2 |
|
Примечание - Средний квадрат отклонений (MS) равен сумме квадратов, деленных на соответствующее число степеней свободы (см. четвертую колонку). В последней колонке указано математическое ожидание среднего квадрата отклонений. |
||||
На рисунке 1 представлен эксперимент с J = 4, К = 3 и L = 2.
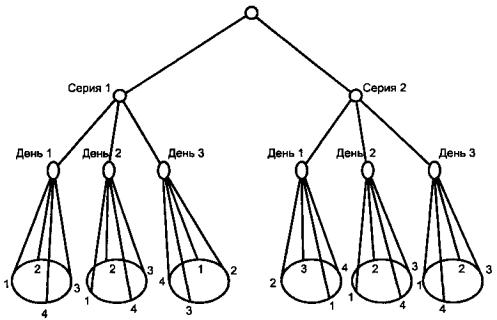
Рисунок 1 - Трехуровневый иерархический эксперимент
5.2.2.2 Эксперимент может быть повторен для Q (Q > 1) выбранных образцов (см. 5.2.3) и для I (I > 1) приборов (средств измерений), если цель состоит в оценке нескольких аналогичных приборов. Преимуществом такого эксперимента является простота использования и легкость вычислений. В частности, количество повторений на каждом уровне не обязательно должно быть большим, так как информацию собирают на нескольких выбранных образцах.
Измерения должны быть выполнены единственным оператором. Действия оператора обычно не сводятся к наблюдению за автоматизированными системами. Однако системы, которые требуют решений относительно линейности, ограничений и других особенностей, могут зависеть от оператора.
Если есть основания предполагать, что результаты, полученные разными операторами, могут существенно различаться, операторы могут выступать в роли серий эксперимента. Выбирают случайным образом L (L > 1) операторов из полного набора операторов, способных выполнять измерения с одним и тем же уровнем прецизионности (следует провести предварительный эксперимент с операторами, выполняющими измерения в условиях повторяемости, и проверить, при необходимости, их сравнительную прецизионность). Затем выполняют сбор и анализ данных. В этом случае стандартное отклонение уровня 3 характеризует влияние оператора.
Проводят случайный отбор средств измерений (приборов) для каждого выбранного образца, т.е. отбирают первый выбранный образец и для него случайным образом отбирают приборы, отбирают второй выбранный образец и для него случайным образом отбирают приборы и т.д.
Записывают выборочное среднее и стандартное отклонение каждой группы из J повторений для выбранного образца и прибора.
Результаты должны быть зарегистрированы вместе с соответствующими данными внешних условий и идентифицированными существенными факторами. Рекомендуется способ регистрации этой информации в одном компьютерном файле в одну строку или ряд информации в фиксированных полях для каждого измерения выбранного образца. Для этих целей полезно использовать крупноформатную таблицу. Типовыми записями являются следующие:
a) месяц;
b) день;
c) год;
d) идентификация оператора;
e) идентификация выбранного образца;
f) идентификация прибора;
g) среднее арифметическое в J повторениях;
h) краткосрочное стандартное отклонение для J повторений;
i) число степеней свободы;
j) показатели внешних условий (при необходимости).
Для модели, описанной выше, стандартное отклонение погрешности ![]() с LK(J - 1) степенями свободы оценивают, используя средний квадрат отклонений случайных ошибок MSE, который вычисляют
следующим образом:
с LK(J - 1) степенями свободы оценивают, используя средний квадрат отклонений случайных ошибок MSE, который вычисляют
следующим образом:
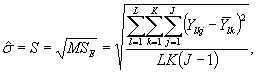
где ![]() - выборочное среднее для каждой группы из J повторений.
- выборочное среднее для каждой группы из J повторений.
Средний квадрат отклонений по дням MSD(R) с L (К - 1) степенями свободы вычисляют по формуле
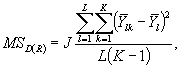
где ![]()
Средний квадрат отклонений по сериям MSR с (L - 1) степенями свободы вычисляют по формуле
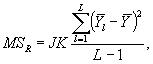
где
![]()
В соответствии с таблицей ANOVA (таблица 1) оценивают стандартное отклонение по дням и по сериям
![]()
![]()
если разность под квадратным корнем положительна. В противном случае ![]() или
или ![]() считают равными нулю.
считают равными нулю.
Иногда для сбора данных о краткосрочных и ежедневных колебаниях процесса измерений используют двухуровневый иерархический эксперимент. Данные этого эксперимента подобны данным, собранным на выбранном образце, описанном в следующем пункте. Если используют более одного выбранного образца, фактор выбранного образца можно рассматривать как случайный, также как фактор «серия» в случае трех уровней. Модель и анализ аналогичны.
5.2.3 Выбранный образец для анализа двух уровней изменчивости
5.2.3.1 Процедура для единственного выбранного образца
Для исследования влияния источников изменчивости, которые проявляются в течение продолжительного времени, рекомендуется использовать измерения на единственном выбранном образце. Сбор и анализ данных являются простыми и не требуют оценки членов, характеризующих взаимодействие в случае зависящих от времени воздействий. Измерения выполняют на двух уровнях, а данных должно быть достаточно для характеристики нескольких измерительных систем. Обычно применяют следующие уровни, характеризующие несколько измерительных систем (уровни должны быть адаптированы к особенностям измерений):
- измерения уровня 1 выполняют в течение короткого срока для оценки прецизионности прибора;
- измерения уровня 2 выполняют в течение нескольких дней для оценки долговременной изменчивости.
Должен быть составлен график проведения измерений на выбранном образце (один раз в день, два раза в неделю или другой в зависимости от того, что необходимо для обеспечения представительности условий измерений), который должен быть выполнен. Измерения на выбранном образце должны быть структурированы, так же как и данные об объектах испытаний, фиксируемые в отчете. Например, если фиксируют среднее арифметическое двух повторений, выполняемых в пределах 5 мин одно после другого, для выбранного образца также следует фиксировать среднее арифметическое двух измерений, выполняемых таким же образом. Однако должно быть выполнено не менее J = 2 повторений в день и т.д. Без такой избыточности данных невозможно проверить краткосрочную прецизионность измерительной системы.
5.2.3.2 Модель
Статистическая модель, описывающая источники исследуемой неопределенности, представляет собой модель сбалансированного двухуровневого иерархического эксперимента
Ykj = μ + δk + εkj
Измерения на объектах испытаний обозначают Ykj (k = 1, ..., К; j = 1, ..., J). Первый индекс указывает день, второй индекс - количество повторений. Члены уравнения, описывающего модель, характеризуют случайные изменения процесса измерений, изменения по дням и краткосрочным временным интервалам. Цель эксперимента состоит в том, чтобы оценить составляющие дисперсии, которые количественно характеризуют эти источники изменчивости.
5.2.3.3 Временные интервалы
Два уровня, рассматриваемые в настоящем подпункте, соответствуют характеристикам нескольких измерительных систем и могут быть адаптированы к конкретным измерениям. Типовая схема эксперимента показана на рисунке 2, где имеется J = 4 повторений в день со следующими уровнями:
- уровень 1: J (J > 1) - краткосрочные повторения для оценки прецизионности прибора;
- уровень 2: К (К > 1) - повторения по дням (или другому соответствующему интервалу времени).
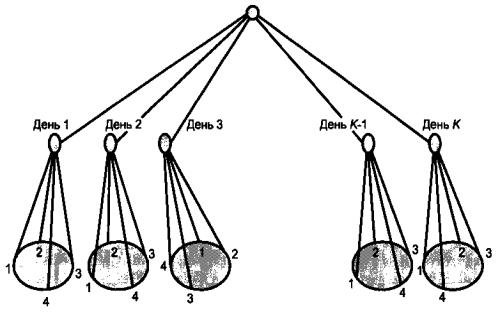
Рисунок 2 - Двухуровневый иерархический эксперимент
5.2.3.4 Сбор данных
Важно, чтобы эксперимент действительно был иерархическим, как показано на рисунке 2, и повторения были выполнены в течение указанных дней. В этом случае достаточно записывать среднее арифметическое и стандартное отклонение для каждой группы повторений J со следующей информацией:
a) месяц;
b) день;
c) год;
d) идентификация оператора;
e) идентификация выбранного образца;
f) идентификация прибора;
g) среднее арифметическое для повторений J;
h) стандартное отклонение повторяемости по J повторениям;
i) число степеней свободы;
j) данные внешних условий (если это необходимо).
Для двухуровневого иерархического эксперимента таблица ANOVA (таблица 2) может быть получена из таблицы для трех уровней.
Таблица 2 - Таблица ANOVA для двухуровневого иерархического эксперимента
|
Источник |
Число степеней свободы v |
Сумма квадратов отклонений SS |
Средний квадрат отклонений MS |
Математическое ожидание среднего квадрата отклонений |
|
День |
К - 1 |
SSD |
MSD |
|
|
Случайная ошибка |
K (J - 1) |
SSE |
MSE |
σ2 |
Стандартное отклонение погрешности с К (J - 1) степенями свободы вычисляют по формуле
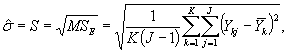
где ![]()
Средний квадрат отклонений для влияния дней MSD с (К - 1) степенями свободы вычисляют по формуле
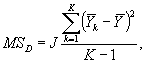
где 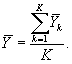
Стандартное отклонение, которое характеризует изменчивость по дням, если разность под квадратным корнем положительна, вычисляют по формуле
![]()
В противном случае ![]() считают равным нулю.
считают равным нулю.
Следствие использования описанной выше классической оценки - возможность появления отрицательных оценок дисперсии. Другие оценки, не имеющие этой особенности, также могут быть использованы.
5.3 Конфигурация измерений
5.3.1 Другие источники неопределенности
Измерения на объектах испытаний обычно выполняют в один день с участием одного оператора с применением одного средства измерений и т.д. Если для характеристики всех измерений, выполняемых в лаборатории, необходимо использовать неопределенность, то ее следует определять для отклонений, соответствующих:
- аппаратуре и средствам измерений;
- операторам;
- геометрическим параметрам;
- другим причинам.
Влияние не поддающихся контролю внешних условий часто можно оценить по данным выбранных образцов, полученным в течение некоторого периода времени. Методы вычисления составляющих неопределенности рассмотрены далее (см. 5.3.3). В настоящем подпункте рассмотрена неопределенность, соответствующая управляемым факторам, таким как операторы или оборудование, использованное для выполнения измерений.
Неопределенность, соответствующая операторам, должна быть исследована только один раз в условиях экспериментов, учитывающих зависимости от времени или зависящих от времени, или при изменении конфигурации измерений. Причинами отклонений в лаборатории с надлежащим обслуживанием могут быть, например, следующие:
- различия в средствах измерений, когда средства измерений не могут быть непосредственно калиброваны в соответствии с исходным эталоном;
- различия, связанные с операторами при выполнении оптических измерений, которые не автоматизированы и результаты которых зависят от особенностей зрительного восприятия оператора;
- различия, связанные с геометрической или электрической конфигурацией оборудования.
Калиброванные средства измерений обычно не попадают в эту группу, поскольку неопределенность, соответствующую калибровке, часто указывают как оценку типа В, а неопределенность средств измерений лаборатории должна укладываться в неопределенность, соответствующую калибровке. Для средств измерений, которые непосредственно не калиброваны, обычно применяют оценку типа А. Эта оценка предназначена для ситуации, когда измерения определены в методике испытаний или стандартной процедуре, использующей средства измерений установленного типа.
Однако следует учесть, что некоторые систематические воздействия не могут быть устранены калибровкой, например влияние матрицы химического состава вещества в аналитической химии.
5.3.2 Важные особенности оценки неопределенности
Различия, упомянутые в начале 5.3.1, рассматривают или как случайные различия, или как смещение. Выбор того или иного подхода зависит, прежде всего, от особенностей задачи. Например, при исследовании влияния на неопределенность оборудования один из подходов состоит в том, чтобы рассматривать оборудование лаборатории как случайную выборку из всей совокупности средств измерений и оценивать неопределенность, относя ее ко всем результатам измерений независимо от того, какие средства измерений использованы для выполнения конкретных измерений. В этом случае может быть применен иерархический двухуровневый эксперимент, где второй уровень характеризует один из источников влияния на неопределенность, а именно оборудование лаборатории. Другой подход состоит в том, чтобы рассматривать неопределенность, соответствующую оборудованию, как смещение (см. 5.5).
Ниже описан простой подход на основе оценки неопределенности одного источника с иерархическим двухуровневым экспериментом.
5.3.3 Сбор данных и вычисление составляющих дисперсии
Для оценки неопределенности процесса измерений, соответствующей применяемому измерительному оборудованию, отбирают случайную выборку I (I > 1). Затем выполняют измерения на Q (Q > 1) объектах с каждым средством измерений. Учитывая все IQ измерений, вычисляют стандартное отклонение Sinst, характеризующее влияние оборудования. Оно имеет (I - 1) степеней свободы.
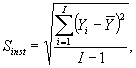
где для i-го средства измерений
![]()
5.3.4 Пример анализа случайных отклонений
Данные измерений удельного сопротивления (Ом·см) пятью зондами (1, 281, 283, 2062, 2362) на Q = 5 пластинах (138, 139, 140, 141, 142) приведены в таблице 3. В 5.5 те же данные проанализированы на смещение. В последнем столбце приведено среднее арифметическое для каждого зонда по всем образцам. Стандартное отклонение средних арифметических результатов измерений удельного сопротивления по зондам составляет 0,0219 Ом·см с четырьмя степенями свободы. Таким образом, Sinst = 0,0219.
Таблица 3 - Результаты измерений удельного сопротивления пяти пластин пятью зондами
Значения в Ом·см
|
Номер зонда |
Идентификационный номер пластины |
Среднее арифметическое |
||||
|
138 |
139 |
140 |
141 |
142 |
||
|
1 |
95,1548 |
99,3118 |
96,1018 |
101,1248 |
94,2593 |
97,1905 |
|
281 |
95,1408 |
99,3548 |
96,0805 |
101,0747 |
94,2907 |
97,1883 |
|
283 |
95,1493 |
99,3211 |
96,0417 |
101,1100 |
94,2487 |
97,1742 |
|
2062 |
95,1125 |
99,2831 |
96,0492 |
101,0574 |
94,2520 |
97,1508 |
|
2362 |
95,0928 |
99,3060 |
96,0357 |
101,0602 |
94,2148 |
97,1419 |
Разности результатов измерений и среднего арифметического для каждого зонда изображают на графике в зависимости от используемой пластины с индивидуальной идентификацией каждого зонда отдельным символом. Анализ графика помогает определить взаимное расположение отклонений, соответствующих конкретному оборудованию, относительно друг друга и оценить, сохраняется ли оно по всем зондам. График, представленный на рисунке 3, построен по данным таблицы 4 (см. 5.5.2.2). Он показывает, что имеются различия по зондам. Например, данные зондов № 2062 и № 2362 расположены ниже, чем данные других зондов.
5.4 Неоднородность материала
5.4.1 Проблемы, связанные с неоднородностью
Образцы, электрические устройства, химические вещества и т.д. могут быть неоднородными относительно исследуемой величины. Неоднородность может быть одним из факторов при оценке неопределенности, если:
a) образец характеризуется единственным значением, но неоднороден по поверхности и т.п.;
b) единственное значение, характеризующее партию, определяют по малой выборке, а партия является неоднородной.
Неоднородность может быть доминирующим источником неопределенности. Даже если процесс измерений очень точен и является статистически управляемым, суммарная неопределенность может быть неприемлемой для практических целей из-за неоднородности материала. Детальные обсуждения исследований однородности для образцов сравнения приведены в ИСО Руководстве 35.
5.4.2 Стратегия случайной неоднородности
Случайную неоднородность оценивают, используя статистические методы для количественной оценки случайных воздействий. Примером неоднородности является образец сравнения химического вещества, который достаточно однороден относительно исследуемых изотопов. Характеристики излучения изотопов определяют по результатам измерений нескольких образцов, случайным образом отобранных из партии.
5.4.3 Сбор данных и вычисление дисперсии, характеризующей неоднородность
Простой схемой для идентификации и количественной оценки влияния неоднородности на результат измерений является сбалансированный двухуровневый иерархический эксперимент. Такой эксперимент предполагает, что К (К > 1) объектов испытаний отобраны случайным образом из партии и J (J > 1) измерений выполнено на каждом объекте испытаний. Полученные результаты измерений обозначают
Yk1, Yk2, …, YkJ, …,YK1, YK2, …, YkJ.
Индекс k = 1,..., К соответствует объектам испытаний и уровню 2, а индекс j = 1,..., J соответствует повторениям измерений на объекте испытаний и уровню 1.
Оценку дисперсии неоднородности, характеризующую неоднородность объектов испытаний, вычисляют как и в 5.2.3, используя методы ANOVA:
![]()
где ![]()
![]()
MSitem - средний квадрат отклонений по объектам испытаний;
![]() - оценка дисперсии, характеризующей неоднородность материала или объектов испытаний.
- оценка дисперсии, характеризующей неоднородность материала или объектов испытаний.
Если разность в числителе ![]() отрицательна, влияние неоднородности считают равным нулю, т.е. неоднородность не дает вклада в неопределенность. Таким образом, для неопределенности, соответствующей неоднородности, справедливо соотношение
отрицательна, влияние неоднородности считают равным нулю, т.е. неоднородность не дает вклада в неопределенность. Таким образом, для неопределенности, соответствующей неоднородности, справедливо соотношение
uinh = max (Sinh, 0).
5.4.4 Оценка неопределенности, соответствующей неоднородности
Оценка неопределенности зависит от характера использования результатов измерений. Как правило, неоднородность важна в тех случаях, когда определяют среднее по нескольким объектам испытаний из партии и это среднее приписывают каждому объекту партии. Для результата измерений, вычисленного как среднее результатов измерений К различных объектов испытаний, стандартную неопределенность uinh, характеризующую неоднородность и соответствующую среднему арифметическому результатов измерений, вычисляют на основе Sinh по формуле
![]()
Однако для результата измерений, вычисляемого как среднее арифметическое результатов измерений К различных объектов испытаний и применяемого к каждому объекту в оставшейся части партии, стандартная неопределенность uinh, являющаяся следствием неоднородности, описывается предикционным интервалом. Таким образом, неопределенность определяют на основе предикционного интервала (см. [2]):
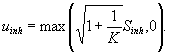
5.4.5 Стратегия в случае системной неоднородности
В случае системной неоднородности требуется другой подход. Например, шероховатость может заметно изменяться на поверхности металлической детали площадью 50 мм2, которая должна иметь установленную шероховатость. Лаборатория может измерить шероховатость на нескольких участках поверхности, но если невозможно описать шероховатость как функцию координат на поверхности, необходимо рассматривать неоднородность как источник неопределенности.
В этой ситуации одна из стратегий состоит в вычислении среднего арифметического результатов измерений шероховатости поверхности детали и оценке неопределенности отклонений от этого значения. Составляющую неопределенности можно оценить одним из нескольких методов оценки неопределенности типа В, приведенных в [1].
5.5 Смещение, соответствующее конфигурации измерений
5.5.1 Основные положения
В статистике для оцениваемого параметра θ смещение оценки ![]() определяют как разность между
математическим ожиданием оценки
определяют как разность между
математическим ожиданием оценки ![]() и истинным значением θ. А именно b = Е[
и истинным значением θ. А именно b = Е[![]() ] - θ. Поскольку истинное значение θ неизвестно, b также неизвестно. Если можно получить оценку b, ее называют поправкой
и обозначают
] - θ. Поскольку истинное значение θ неизвестно, b также неизвестно. Если можно получить оценку b, ее называют поправкой
и обозначают ![]() . Поправка может относиться к объекту сравнения или к некоторому среднему значению. Зная ряд поправок
. Поправка может относиться к объекту сравнения или к некоторому среднему значению. Зная ряд поправок ![]() 1, ...,
1, ..., ![]() n, смещение оценки можно оценить:
n, смещение оценки можно оценить:
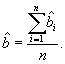
Если поправки рассматривают как случайные величины, для описания их распределения можно использовать нормальное распределение.
Если поправки близки к нулю, часто предполагают, что распределение вероятностей для поправок имеет нулевое среднее (математическое ожидание). Этот случай часто называют «нулевой»
поправкой. В этом случае ![]() является несмещенной оценкой θ. Если поправки распределены по нормальному закону или имеется большое количество известных поправок, неопределенность смещения
может быть оценена с помощью стандартного отклонения выборочного среднего (среднего арифметического) поправок. Если нет достаточной информации о распределении, можно предположить, что
поправки {
является несмещенной оценкой θ. Если поправки распределены по нормальному закону или имеется большое количество известных поправок, неопределенность смещения
может быть оценена с помощью стандартного отклонения выборочного среднего (среднего арифметического) поправок. Если нет достаточной информации о распределении, можно предположить, что
поправки {![]() i, i = 1,..., n} равномерно распределены между (-а) и (+а). Оценка смещения в этом случае равна нулю. Оценку â определяют по формуле
i, i = 1,..., n} равномерно распределены между (-а) и (+а). Оценка смещения в этом случае равна нулю. Оценку â определяют по формуле
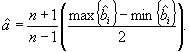
Оценкой стандартного отклонения оценки смещения ![]() является
является ![]() :
:
![]()
Применительно к метрологии источники смещения, рассматриваемые в настоящих рекомендациях, охватывают установленные конфигурации измерений. Измерения на объектах испытаний обычно выполняет один оператор в один день с использованием единственного средства измерений и т.д. Даже если неопределенность должна быть использована для характеристики результатов измерений, выполненных в одной конкретной конфигурации, необходимо объяснять любые существенные различия, связанные:
a) с оборудованием,
b) с операторами,
c) с конфигурацией,
d) с другими причинами.
Оборудование, применяемое при калибровке, обычно не попадает в эту группу, поскольку неопределенность, соответствующую калибровке, обычно указывают как оценку типа В, а неопределенность оборудования лаборатории должна укладываться в неопределенность, соответствующую калибровке. Некалиброванное оборудование больше подходит для оценки типа А. Эта оценка предназначена для ситуации, когда измерения определены в методике испытаний или в стандартной процедуре с использованием оборудования установленного типа.
Если рассматривать измерения только одной конфигурации, например измерения с применением установленного средства измерений, или если требуется меньшая неопределенность, среднее отклонение обрабатывают как смещение. Одна из стратегий в такой ситуации состоит в том, чтобы скорректировать измерения, выполненные с применением установленного средства измерений, на среднее арифметическое для оборудования лаборатории и оценить неопределенность типа А. Эта стратегия опирается на предположение о том, что оборудование лаборатории представляет собой случайную выборку из всего оборудования установленного типа.
Однако ситуация, при которой возможно сравнение двух единиц оборудования и ни для одной из них неизвестно, имеется ли у нее смещение, требует другой стратегии, поскольку среднее арифметическое не обязательно даст несмещенный результат. Рекомендованная стратегия, если есть существенное различие между единицами оборудования (что необходимо проверить), состоит в том, чтобы применить «нулевую» поправку и оценить неопределенность типа А, соответствующую поправке.
Таким образом, существует много возможных сценариев для описания смещений, которые следует время от времени анализировать. План необходим для следующего:
- сбора данных;
- тестов для анализа смещений (графических или статистических);
- оценки смещений;
- оценки неопределенности, соответствующей существенным смещениям.
Без потери общности в настоящих рекомендациях оборудование рассматривается как единственный источник смещения. Рассмотрим сначала ситуацию с моделью измерений для одного средства измерений. Обозначим Y1,..., Yn - независимые измерения истинной величины θ, для измерения которой применяют единственное средство измерений, а μ - среднее арифметическое большого количества независимых измерений с использованием этого средства измерений. Таким образом
Yi = μ + ei
где е1, ..., еn - независимо распределенные случайные ошибки (погрешности) с нулевым средним и дисперсией σ2.
Выборочное среднее ![]() используют в качестве оценки θ, и фиксируют результат для применяемого средства измерений:
используют в качестве оценки θ, и фиксируют результат для применяемого средства измерений: ![]() . Ошибку (погрешность) использования
. Ошибку (погрешность) использования ![]() в качестве θ можно
представить в виде
в качестве θ можно
представить в виде
![]()
где ![]()
b = μ - θ.
Следовательно,
![]()
Здесь ![]() - случайная составляющая, a b - систематическая составляющая или смещение, соответствующее применяемому средству измерений. Неопределенность, соответствующую случайной
составляющей
- случайная составляющая, a b - систематическая составляющая или смещение, соответствующее применяемому средству измерений. Неопределенность, соответствующую случайной
составляющей ![]() , обычно оценивают как u(
, обычно оценивают как u(![]() ) = S/
) = S/![]() , предполагая нормальное распределение ошибки, где S - оценка стандартного отклонения по выборке Y1, ..., Yn. Неопределенность, соответствующую
, предполагая нормальное распределение ошибки, где S - оценка стандартного отклонения по выборке Y1, ..., Yn. Неопределенность, соответствующую
![]() (оценке b), оценивают на основе научных исследований и оценки неопределенности типа В или
используя статистические методы и оценку неопределенности типа А. Для случая с одним средством
измерений часто удобно устанавливать неопределенность
(оценке b), оценивают на основе научных исследований и оценки неопределенности типа В или
используя статистические методы и оценку неопределенности типа А. Для случая с одним средством
измерений часто удобно устанавливать неопределенность ![]() , используя распределение с нулевым
средним. Если это среднее известно и равно b, то каждое измеренное значение Yi - может быть скорректировано на значение b, т.е. заменено на (Yi - b). Таким образом, предположение о том, что b имеет нулевое среднее, не является ограничением. Распределение b можно считать нормальным или равномерным, или некоторым другим. Суммарную неопределенность
, используя распределение с нулевым
средним. Если это среднее известно и равно b, то каждое измеренное значение Yi - может быть скорректировано на значение b, т.е. заменено на (Yi - b). Таким образом, предположение о том, что b имеет нулевое среднее, не является ограничением. Распределение b можно считать нормальным или равномерным, или некоторым другим. Суммарную неопределенность ![]() , как оценку θ, тогда вычисляют по
формуле
, как оценку θ, тогда вычисляют по
формуле
![]()
где ub - неопределенность b, основанная на оценках типа А и/или типа В. Соответствующее число степеней свободы вычисляют, используя формулу Велча-Саттервейтта.
Рассмотрим измерения, выполненные К средствами измерений. Тогда Yki (k = 1,..., К; i = 1,..., n) представляют собой независимые измерения, выполненные k-м средством измерений. Соответствующая статистическая, модель имеет вид
Yki = θ + bk + eki,
где bk - смещение, соответствующее k-му (k = 1,..., К) средству измерений, a eki - случайные ошибки. Цель состоит в оценке bk и соответствующей неопределенности. Решение задачи зависит от предположений относительно bk, рассмотренных в 5.5.2 и 5.5.3. В 5.5.4 рассмотрено смещение с дополнительными данными.
5.5.2 Постоянное смещение
5.5.2.1 Основные положения
Смещение можно рассматривать как постоянное или непостоянное. Если смещение сохраняет свое значение в течение длительного времени или имеет одно и то же значение для конкретного средства измерений, его называют постоянным смещением. На постоянное смещение следует корректировать результаты измерений, если смещение можно достаточно точно оценить по результатам повторных измерений. Это предполагает, что значение смещения для соответствующего оборудования по существу одинаково для всех исследуемых материалов. Результаты измерений
Yki (k = 1, ..., К; i =1, ..., n)
означают, что измерения выполнены на n образцах с применением К единиц оборудования. Статистическая модель, данная в 5.5.1, имеет вид
Yki = θ + bk + еki,
где θ - значение измеряемой величины Y; bk - смещение k-й единицы оборудования, a eki - случайная ошибка, если считать, что смещения bk являются неслучайными, т.е. постоянными. Из приведенной выше модели следует, что ![]() , т.е.
, т.е.
![]()
где 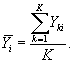
Для i-го образца оценкой θ может быть ![]() а поправка для i-го образца и k-й единицы оборудования
а поправка для i-го образца и k-й единицы оборудования ![]() . Здесь результат измерений i-го образца с помощью k-й единицы оборудования скорректирован на среднее для всех К единиц оборудования. В соответствии с приведенной выше
моделью смещение bк k-й единицы оборудования:
. Здесь результат измерений i-го образца с помощью k-й единицы оборудования скорректирован на среднее для всех К единиц оборудования. В соответствии с приведенной выше
моделью смещение bк k-й единицы оборудования:
![]()
где ![]()
Поправка, которую необходимо применять к результатам измерений, выполненных с использованием k-й единицы оборудования, имеет вид
![]()
где Yкорр - скорректированное значение Y;
Yизм - значение результата измерений.
Неопределенность смещения или среднего арифметического поправок для k-й единицы оборудования имеет вид
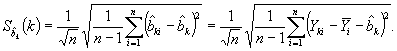
Для проверки значимости смещения может быть применен статистический критерий.
5.5.2.2 Пример постоянного смещения
В примере рассмотрен случай, когда измерения выполнены с применением одной единицы оборудования (одного средства измерений), а фиксируемые значения скорректированы на смещение, соответствующее этому оборудованию. Ситуацию, когда любой из имеющихся зондов может быть использован для выполнения измерений, рассматривают как результат случайных воздействий.
В таблице 4 среднее арифметическое для каждой кремниевой пластины вычтено из каждого
результата измерений. Измерения удельного сопротивления (Ом·см) были выполнены с использованием пяти зондов на каждой из пяти кремниевых пластин. Корректировка, как показано выше, характеризует отличие каждого конкретного зонда от других, т.е. ![]() для k-го зонда и i-й пластины. Значения b5i (i = 1, ..., 5) для зонда № 2362 постоянны и отрицательны для всех пяти пластин.
для k-го зонда и i-й пластины. Значения b5i (i = 1, ..., 5) для зонда № 2362 постоянны и отрицательны для всех пяти пластин.
Таблица 4 - Поправки ![]() для зондов и кремниевых пластин
для зондов и кремниевых пластин
Значения в Ом·см
|
Номер зонда |
Идентификаци- |
Идентификационный номер пластины |
||||
|
138 |
139 |
140 |
141 |
142 |
||
|
1 |
1 |
0,02476 |
-0,00356 |
0,04002 |
0,03938 |
0,00620 |
|
181 |
2 |
0,01076 |
0,03944 |
0,01871 |
-0,01072 |
0,03761 |
|
182 |
3 |
0,01926 |
0,00574 |
-0,02008 |
0,02458 |
-0,00439 |
|
2062 |
4 |
-0,01754 |
-0,03226 |
-0,01258 |
-0,02802 |
-0,00110 |
|
2362 |
5 |
-0,03725 |
-0,00936 |
-0,02608 |
-0,02522 |
-0,03830 |
Для исследования зонда № 2362:
- смещение 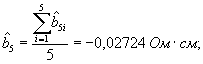
- стандартное отклонение поправок ![]() = 0,01171 для любого i;
= 0,01171 для любого i;
- стандартное отклонение смещения ![]() (или среднего поправки)
(или среднего поправки) ![]() .
.
Разности результатов измерений и среднего арифметического [т.е. поправки (![]() )] изображены
на графике (см. рисунок 3) в соответствии с идентификационным номером пластины.
)] изображены
на графике (см. рисунок 3) в соответствии с идентификационным номером пластины.
При этом каждому зонду присвоен свой идентификационный номер. График рисунка 3 подтверждает, что зонд № 2362 (на графике отмечен цифрой 5) для данного процесса измерений постоянно дает более низкие результаты, чем другие. Такое положение сохраняется в течение двух серий, которые отделены друг от друга двумя месяцами.
Поскольку имеется существенное и постоянное смещение для зонда № 2362, измерения, выполненные с применением этого зонда, должны быть скорректированы на среднее арифметическое смещений результатов измерений относительно других зондов.
5.5.3 Непостоянное смещение
5.5.3.1 Основные положения
Если смещение для конкретного средства или конфигурации измерений является существенным и имеет случайный характер, его рассматривают как непостоянное. Без потери общности среднее смещения можно считать равным нулю. В противном случае его можно корректировать, вычитая оценку смещения из результатов измерений. Таким образом, может быть принято предположение о нулевом среднем. Для определения неопределенности смещения необходимо знать распределение поправок (нормальное или равномерное распределение) в соответствии с 5.5.1. В 5.5.3.2 приведен пример «нулевой» корректировки. Другой вид непостоянного смещения описан в 5.5.4.
5.5.3.2 Пример непостоянного смещения
В качестве исходных данных использованы результаты измерений удельного сопротивления с помощью пяти зондов на пяти кремниевых пластинах. В таблице 5 приведены поправки или смещения для зонда № 283, который является исследуемым зондом на уровне, где объекты - пластины с удельным сопротивлением 1 Ом·см, вычисленным по всем зондам, как показано в 5.5.2.
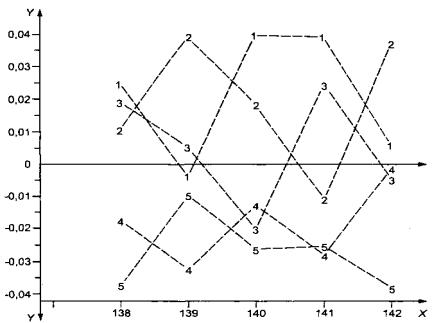
X - идентификационный номер пластины; Y - ![]() (Ом·см); 1, .... 5 - идентификационные номера зондов (см. таблицу 4)
(Ом·см); 1, .... 5 - идентификационные номера зондов (см. таблицу 4)
Рисунок 3 -
График поправок ![]() в соответствии с
идентификационным
номером пластин для
пяти зондов
в соответствии с
идентификационным
номером пластин для
пяти зондов
Среднее арифметическое поправок отрицательно для серии 1 и положительно для серии 2 с интервалом между сериями в два месяца.
Таблица 5 - Смещения для зонда № 283
Значения в Ом·см
|
Идентификационный номер пластины |
Серия 1 |
Серия 2 |
|
11 |
0,0000340 |
-0,0001841 |
|
26 |
-0,0001000 |
0,0000861 |
|
42 |
0,0000181 |
0,0000781 |
|
131 |
-0,0000701 |
0,0001580 |
|
208 |
-0,0000240 |
0,0001879 |
|
Среднее арифметическое |
-0,0000284 |
0,0000652 |
Применение t-критерия к парам значений для серий 1 и 2 в предположении, что поправки
{![]() , i = 1, 2, 3, 4, 5} подчиняются нормальному распределению, не отклоняет гипотезу о том, что
серия 1 и серия 2 имеют одинаковое среднее. Объединяя поправки двух серий, вычисляют статистику
t = 0,5016 с девятью степенями свободы. Таким образом, гипотеза о нулевом среднем не отклоняется с
ошибкой 5 %. Оценка смещения для зонда № 283 составила 0,0000184 Ом·см, а оценка стандартного
отклонения смещения
, i = 1, 2, 3, 4, 5} подчиняются нормальному распределению, не отклоняет гипотезу о том, что
серия 1 и серия 2 имеют одинаковое среднее. Объединяя поправки двух серий, вычисляют статистику
t = 0,5016 с девятью степенями свободы. Таким образом, гипотеза о нулевом среднем не отклоняется с
ошибкой 5 %. Оценка смещения для зонда № 283 составила 0,0000184 Ом·см, а оценка стандартного
отклонения смещения ![]() = 0,000031 Ом см. Альтернативное предположение состоит в том, что
поправки попадают в область ± а, где оценка â = 0,0002273 получена по формуле, приведенной в 5.5.1. В этом случае оценка смещения для зонда № 283 равна нулю, а стандартное отклонение оценки смещения имеет вид
= 0,000031 Ом см. Альтернативное предположение состоит в том, что
поправки попадают в область ± а, где оценка â = 0,0002273 получена по формуле, приведенной в 5.5.1. В этом случае оценка смещения для зонда № 283 равна нулю, а стандартное отклонение оценки смещения имеет вид
![]()
5.5.4 Смещение по малому объему данных
5.5.4.1 Основные положения
В настоящем пункте рассмотрен метод определения смещений, для которых трудно получить достоверные оценки из-за недостаточного количества данных. Например, испытания на двух из многих возможных конфигураций процесса измерений не могут дать достоверную оценку смещения для корректировки, но могут выявить проблемы в процессе измерений. Если смещение существенное, стратегия зависит от того, постоянным или переменным оно является.
5.5.4.2 Пример смещения
Пример описывает исследование регулировки единственного прибора. Прибор - четырехточечный зонд, используемый для измерения удельного сопротивления кремниевых пластин, может быть отрегулирован несколькими способами. Поскольку не было возможности проверить все конфигурации в процессе градуировки прибора, были выполнены измерения только для двух конфигураций.
Измерения были выполнены на пяти пластинах за шесть дней (за исключением пластины 39 во второй день) зондом № 2062 для двух конфигураций. Разности результатов измерений для этих двух конфигураций в один и тот же день скорректированы поправками и приведены в таблице 6.
График разностей для этих двух конфигураций приведен на рисунке 4. Из рисунка видно, что эти разности в основном отрицательны. Максимум и минимум разностей составили 0,0044 и (-0,0155). Смещение, соответствующее конфигурациям, оценивают средним арифметическим поправок
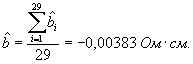
Таблица 6 - Разности результатов измерений в двух конфигурациях (зонд № 2062)
|
Пластина |
Идентификационный номер пластины |
День |
Разность результатов измерений |
|
17 |
1 |
1 |
-0,0108 |
|
2 |
-0,0111 |
||
|
3 |
-0,0062 |
||
|
4 |
0,0020 |
||
|
5 |
0,0018 |
||
|
6 |
0,0002 |
||
|
39 |
2 |
1 |
-0,0089 |
|
3 |
-0,0040 |
||
|
4 |
-0,0022 |
||
|
5 |
-0,0012 |
||
|
6 |
-0,0034 |
||
|
63 |
3 |
1 |
-0,0016 |
|
2 |
-0,0111 |
||
|
3 |
-0,0059 |
||
|
4 |
-0,0078 |
||
|
5 |
-0,0007 |
||
|
6 |
0,0006 |
||
|
103 |
4 |
1 |
-0,0050 |
|
2 |
-0,0140 |
||
|
3 |
-0,0048 |
||
|
4 |
0,0018 |
||
|
5 |
0,0016 |
||
|
6 |
0,0044 |
||
|
125 |
5 |
1 |
-0,0056 |
|
2 |
-0,0155 |
||
|
3 |
-0,0010 |
||
|
4 |
-0,0014 |
||
|
5 |
0,0003 |
||
|
6 |
-0,0017 |
Так как общее количество разностей 29, неопределенность смещения, основанная на выборочном стандартном отклонении
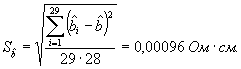
Значение t-статистики для 29 поправок (![]() ) равно (-4,0133). Гипотеза, о том, что распределение
поправок имеет среднее, равное нулю, отклонена.
) равно (-4,0133). Гипотеза, о том, что распределение
поправок имеет среднее, равное нулю, отклонена.
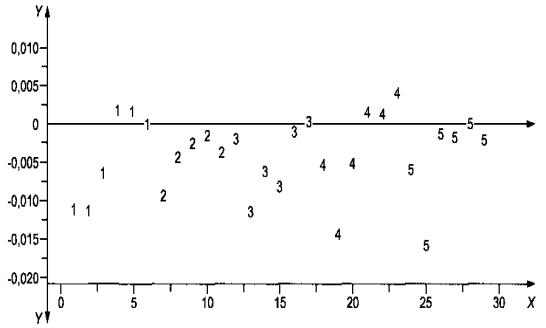
X - время, дни; Y - разность удельного сопротивления в двух конфигурациях, Ом·см; 1,..., 5 - идентификационные номера пластин (см. таблицу 6)
Рисунок 4 - Разности результатов измерений в двух конфигурациях (серия измерений выполнена зондом № 2062 на пяти пластинах в течение шести дней)
6 Оценка неопределенности типа В
6.1 Оценки неопределенности типа В применяют как к случайным, так и к систематическим воздействиям на результаты измерений. Отличительной особенностью оценок типа В является то, что вычисление составляющей неопределенности не основано на статистическом анализе данных.
Некоторые примеры источников неопределенности, для которых применяют оценку типа В:
- исходные эталоны, калиброванные другой лабораторией;
- физические константы, используемые при вычислении регистрируемого значения;
- воздействия окружающей среды, по которым может быть сформирована выборка;
- возможная некоаксиальность конфигурации/геометрии оборудования;
- недостаточная разрешающая способность оборудования.
6.2 Документированные источники неопределенности, такие как отчеты о калибровке для исходных эталонов или опубликованные отчеты о неопределенности физических констант, не представляют трудностей для анализа. Неопределенность в этом случае указывают как расширенную неопределенность U, которую преобразуют в стандартную неопределенность и по формуле
![]()
Если коэффициент k неизвестен, ему можно присвоить гарантированное значение k = 2. Для источников неопределенности, являющихся локальными по отношению к процессу измерений, по которым не может быть отобрана выборка, необходимая для статистического анализа, применяют оценки типа В. Одним из широко используемых методов является оценка влияния наихудшей ситуации на основе:
- опыта;
- научных исследований;
- имеющихся данных.
6.3 В исследуемой ситуации оцениваемое смещение или поправку можно рассматривать как случайную величину, подчиняющуюся установленному распределению. В этом случае стандартная неопределенность равна стандартному отклонению этого распределения. Среди возможных распределений рассматривают только два: равномерное и треугольное.
а) Равномерное распределение

В случае равномерного распределения все возможные значения лежат между (-а) и (+а) и одинаково вероятны. Значения границ распределения (±а) известны.
![]()
Число степеней свободы может быть принято равным бесконечности, если а точно известно. В противном случае выбранное число степеней свободы должно отражать точность, с которой известно значение а (см. [1], пункт G 4.2.).
b) Треугольное распределение
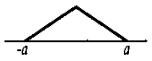
![]()
При равных границах треугольное распределение дает меньшую стандартную неопределенность, чем равномерное распределение.
Число степеней свободы обычно принимают равным бесконечности.
7 Распространение неопределенности
7.1 Основные положения
7.1.1 Изложенный выше подход к оценке неопределенности называют нисходящим. Составляющие неопределенности оценивают на основе повторных измерений. Отличия от закона распространения неопределенности очевидны в следующем простом примере, когда границы прямоугольного распределения оценивают на основе повторения пары измерений - длины L и ширины W. Площадь A
A = L·W
может быть вычислена по каждому повторению. Стандартное отклонение регистрируемой площади оценивают непосредственно на основе повторений.
7.1.2 Преимуществами этого подхода являются следующие возможности:
- надлежащая обработка ковариаций между результатами измерений длины и ширины;
- надлежащая обработка источников неопределенности, которые должны проявиться, если измерения охватывают всю область эксплуатационных режимов и достаточно длинный период времени.
7.1.3 Иногда измерения невозможно повторить так, чтобы учесть все воздействия на их результаты. Можно воспользоваться рекомендациями по применению закона распространения неопределенности ([1]). В этом случае рекомендуется вычислить:
a) результат измерений как произведение средней длины на среднюю ширину;
b) стандартную неопределенность, соответствующую длине L;
c) стандартную неопределенность, соответствующую ширине W, -
и объединить эти две стандартные неопределенности в стандартную неопределенность, соответствующую результату измерений, используя приближение для произведения двух переменных. При отсутствии ковариаций между измерениями длины и ширины применяют формулу
![]()
7.1.4 В идеальном случае найденное значение не будет сильно отличаться от полученного при выполнении измерений площади. Однако иногда различия могут быть очень существенными по следующим причинам:
- наличие неизвестных ковариаций;
- плохая организация работ, влияющая на ведение записей измеряемой величины;
- ошибки округления.
В общем случае закон распространения неопределенности использует модель в виде функции одной или нескольких переменных X, Z, ...
Y = f (X, Z, ...)
Эта модель позволяет определить оценки стандартного отклонения Y в следующем виде:
![]()
где SX - стандартная неопределенность, соответствующая X;
SZ - стандартная неопределенность, соответствующая Z;
SXZ - ковариация X и Z;
∂f/∂X - частная производная функции f (X, Z,...) по Х в точке (X, Z,...) наилучших оценок Х, Z,... и т.д.
7.1.5 Ковариацию может быть трудно оценить, если измерения не выполнены в парах. Иногда эти члены в формуле бывают опущены. Это приемлемо в следующих случаях:
a) если измерения X, Z статистически независимы, ковариация равна нулю;
b) члены с ковариацией должны быть включены в расчеты, только если они были оценены по достаточному количеству данных или если имеется другая информация, допускающая их определение.
Обычно значения, регистрируемые в экспериментах по калибровке, имеют ковариации, отличные от нуля, которые необходимо учитывать, если Y является суммой, например суммой двух масс или длин двух блоков и т.п.
7.2 Формулы для функции единственной переменной
Стандартные отклонения величин, которые являются функциями одной переменной, приведены в таблице 7, составленной на основе [3]. Величина Y является функцией выборочного среднего N результатов измерений одной переменной.
7.3 Формулы для функции двух переменных
Стандартные отклонения величин, которые являются функциями двух переменных, приведены в таблице 8, составленной на основе [3]. Величина Y является функцией выборочного среднего N результатов измерений двух переменных. Множители стандартных отклонений обычно называют «коэффициентами чувствительности».
Таблица 7 - Стандартные отклонения для функции одной переменной
|
Функция Y от |
Первое приближение стандартного отклонения Y |
Примечания |
|
|
SX - выборочное стандартное отклонение X |
- |
|
Y = |
|
- |
|
|
|
- |
|
|
|
- |
|
|
|
- |
|
|
|
- |
|
|
|
Для малых N приближение является очень грубым |
|
|
|
Предполагается, что X подчиняется нормальному распределению (см. [4]) |
Таблица 8 - Стандартное отклонение для функции двух переменных
|
Функция Y от |
Стандартное отклонение Y |
|
|
SX - выборочное стандартное отклонение X SZ - выборочное стандартное отклонение Z
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а) Ковариацию необходимо включать только при наличии достоверной оценки. |
|
8 Примеры. Оценка неопределенности типа А
8.1 Цель и предпосылки
Целью данного исследования является демонстрация оценки неопределенности процесса измерений с несколькими источниками неопределенности. Рассматриваемые результаты измерений - значения удельного сопротивления (Ом·см) кремниевых пластин. Необходимо вычислить неопределенность результатов измерений удельного сопротивления приблизительно 100 кремниевых пластин, сертифицированных с помощью зонда с четырьмя точками, объединенными в определенную конфигурацию, называемую конфигурацией А, в соответствии с методом F84 ASTM, рекомендованным для этих измерений. Фиксируемое для каждой пластины значение - среднее арифметическое шести краткосрочных повторений, выполненных в центре пластины. Измерения были проведены в Национальном институте стандартов и технологии (NIST) с использованием зонда № 2362 - одного из пяти зондов NIST.
Оценка неопределенности учитывает следующие зависящие от времени источники изменчивости:
a) краткосрочные воздействия измерений в центре пластины;
b) изменения по дням;
c) изменения от серии к серии,
а также следующие возможные источники смещения:
- смещение, характерное для зонда № 2362;
- смещение, соответствующее конфигурации А.
8.2 Сбор данных и выбранный образец
8.2.1 Сертификационные измерения непосредственно не являются первичным источником для оценок зависящих от времени составляющих неопределенности, поскольку они не дают информации о ежедневных и долгосрочных воздействиях. Три зависящих от времени источника неопределенности оценены на основе данных иерархического эксперимента с тремя уровнями:
- J = 6 измерений в центре пластины;
- К = 6 дней;
- L = 2 серии.
Модель для трехуровневого эксперимента имеет вид:
Ylkj = μ + γl + δlk + εlkj,
где l = 1, 2; k = 1, .., 6 и j = 1, .., 6.
8.2.2 Эксперимент повторяют на каждой из М = 5 пластин, выбранных наугад из партии пластин. Выбранные образцы идентифицированы номерами 138, 139, 140, 141 и 142. Эксперимент также повторяют с пятью (Q = 5) зондами с номерами 1, 281, 283, 2062, 2362. Данные включают в себя:
- номер серии;
- идентификационный номер пластины;
- месяц и день выполнения измерений;
- сведения об операторе;
- значение температуры;
- среднее арифметическое результатов шести измерений в центре пластины;
- краткосрочное (повторяемость) стандартное отклонение результатов шести измерений.
8.3 Анализ повторяемости ежедневных и долгосрочных воздействий
Сравнивают прецизионность зонда № 2362 и других зондов и проверяют, изображая на графике, стандартные отклонения повторяемости для каждого зонда в соответствии с идентификационным номером пластины. Зонд № 2362 продемонстрировал лучшую прецизионность для серии 1, и поэтому он выбран для сертификационных измерений. Однако вклад прецизионности в неопределенность не является единственным или самым важным.
Здесь воздействие пластин предполагается фиксированным. Иерархическому трехуровневому эксперименту с воздействием пластин соответствует смещенная модель, которая отличается от модели, описанной в 5.2.2. В таблице 9 приведены оценки ANOVA.
Таблица 9 - Таблица ANOVA для исследования данных
|
Источник |
Число степеней свободы v |
Средний квадрат отклонений MS |
Математическое ожидание среднего квадрата отклонений |
|
Серия |
1 |
MSR = 0,009198 |
|
|
День (серия) |
10 |
MSD(R) = 0,003238 |
|
|
Случайная ошибка |
44 |
MSE = 0,0008046 |
σ2 |
|
Примечание - В данном примере совместные воздействия не рассматриваются. Такие воздействия должны быть включены, если предполагается, что источники могут влиять один на другой. Например, при наличии двух лекарств одно может купировать действие другого. |
|||
Составляющие дисперсии, соответствующие воздействию повторяемости дней и серий, также получены:
![]()
![]()
![]()
8.4 Смещение, соответствующее зонду
8.4.1 Графический анализ
Прецизионность зонда рассмотрена в 8.1. В настоящем пункте исследовано смещение зонда. Графический анализ показывает относительные смещения зондов (см. рисунок 3). Для каждой пластины разности со средним арифметическим всех пластин изображены на графике в соответствии с идентификационным номером пластины для каждого зонда. Графики подтверждают, что зонд № 2362, отмеченный цифрой 5, смещен относительно других зондов, ему всегда соответствуют более низкие значения. Смещение становится более очевидным в серии 2. Идентификационные номера зондов и их заводские номера:
1 - № 1;
2 - № 281;
3 - № 283;
4 - № 2026;
5 - № 2362.
8.4.2 Количественный анализ
Поправки для пяти зондов приведены в таблице 10 как отклонения от среднего арифметического
для каждой пластины. Для конкретной серии в таблице приведены значения ![]() , как определено
в 5.5.2 для k = 1, 2, 3, 4, 5 (зонды №1, №281, №283, №2026, №2362) и
i = 138, 139, 140, 141, 142.
, как определено
в 5.5.2 для k = 1, 2, 3, 4, 5 (зонды №1, №281, №283, №2026, №2362) и
i = 138, 139, 140, 141, 142.
Таблица 10 - Смещения для пяти зондов
|
Номер пластины |
Идентификационный номер пластины |
Номер зонда |
Серия 1 |
Серия 2 |
|
138 |
1 |
1 |
0,0248 |
-0,0119 |
|
281 |
0,0108 |
0,0323 |
||
|
283 |
0,0193 |
-0,0258 |
||
|
2062 |
-0,0175 |
0,0561 |
||
|
2362 |
-0,0372 |
-0,0507 |
||
|
139 |
2 |
1 |
-0,0036 |
-0,0007 |
|
281 |
0,0394 |
0,0050 |
||
|
283 |
0,0057 |
0,0239 |
||
|
2062 |
-0,0323 |
0,0373 |
||
|
2362 |
-0,0094 |
-0,0657 |
||
|
140 |
3 |
1 |
0,0400 |
0,0109 |
|
281 |
0,0187 |
0,0106 |
||
|
283 |
-0,0201 |
0,0003 |
||
|
2062 |
-0,0126 |
0,0182 |
||
|
2362 |
-0,0261 |
-0,0398 |
||
|
141 |
4 |
1 |
0,0394 |
0,0324 |
|
281 |
-0,0107 |
-0,0037 |
||
|
283 |
0,0246 |
-0,0191 |
||
|
2062 |
-0,0280 |
0,0436 |
||
|
2362 |
-0,0252 |
-0,0534 |
||
|
142 |
5 |
1 |
0,0062 |
0,0093 |
|
281 |
0,0376 |
0,0174 |
||
|
283 |
-0,0044 |
0,0192 |
||
|
2062 |
-0,0011 |
0,0008 |
||
|
2362 |
-0,0383 |
-0,0469 |
8.4.3 Корректировка смещения зонда
Зонд № 2362 был выбран для сертификационных измерений, поскольку ему соответствует наилучшая прецизионность. Однако этот зонд имеет смещение относительно других зондов. Существует два способа устранения смещения зонда:
a) корректировать все результаты измерений, выполненных с зондом № 2362 с учетом среднего арифметического всех зондов;
b) включить стандартное отклонение, характеризующее воздействие зондов, в оценку неопределенности.
Лучшим выбором является способ перечисления а), если можно предположить, что зонды представляют собой случайную выборку из всех зондов данного типа, особенно если учесть, что единица измерений (удельного сопротивления) определяется методом испытаний. Поэтому следует корректировать все результаты измерений на смещение среднего арифметического для зонда № 2362 и вычислить по этим данным оценку неопределенности типа А.
Поправки для зонда № 2362 по таблице 10 показаны в таблице 11. Все поправки отрицательные. Анализ поправок двух серий с помощью критерия знаков показывает, что они принадлежат одной генеральной совокупности.
Таблица 11 - Смещения для зонда № 2362
|
Номер пластины |
Серия 1 |
Серия 2 |
Обе серии вместе |
|
138 |
-0,0372 |
-0,0507 |
|
|
139 |
-0,0094 |
-0,0657 |
|
|
140 |
-0,0261 |
-0,0398 |
|
|
141 |
-0,0252 |
-0,0534 |
|
|
142 |
-0,0383 |
-0,0469 |
|
|
Среднее арифметическое |
-0,0272 |
-0,0513 |
-0,0393 |
|
Дисперсия |
0,0002618 |
||
|
Стандартное отклонение |
0,01618 |
||
Оценка смещения зонда № 2362 равна -0,0393. Неопределенность смещения зонда № 2362
|
|
8.5 Формирование смещения
8.5.1 Измерения с двумя конфигурациями зонда
Сертификационные измерения были выполнены с зондом № 2362, собранным в определенной конфигурации, названной конфигурацией А. Исследование было выполнено с зондом № 2362, собранным двумя способами для лучшего выявления различий. Необработанные данные, соответствующие обеим конфигурациям, приведены в настоящем стандарте.
8.5.2 Графический анализ
Разности измерений в конфигурациях А и В, выполненных в один и тот же день, изображены на графике для каждой пластины. На рисунке 5 показаны две серии измерений удельного сопротивления, выполненных приблизительно через два месяца одно после другого. Точки данных расположены случайным образом выше и ниже нулевой линии и не указывают на различия между конфигурациями. Поэтому вклад в неопределенность этого источника может быть оценен как незначительный.
8.5.3 Количественный тест на различие конфигураций
Различия исследованы с помощью t-критерия на основе таблицы 12, где средние арифметические и стандартные отклонения разностей вычислены по результатам измерений, выполненных в течение шести дней на пяти пластинах. Статистика t-критерия принимает значение 2, что не указывает на наличие существенной разницы в данных для этих двух конфигураций. Вывод: смещение, соответствующее конфигурации, отсутствует, а вклад его в неопределенность является несущественным.
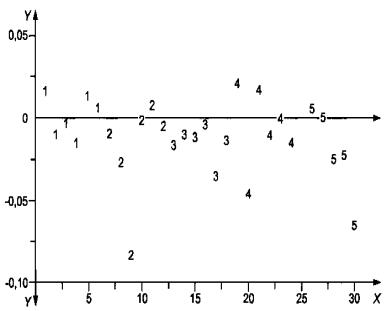
а) Серия 1
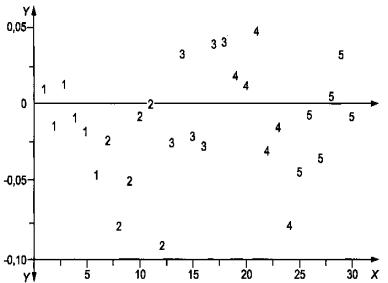
b) Серия 2
X - время (дни); Y - разности результатов измерений удельного сопротивления, Ом·см; 1, ..., 5 - идентификационные номера пластин (см. таблицу 10)
Рисунок 5 - Разности результатов измерений, выполненных в конфигурациях А и В
Таблица 12 - Различия двух конфигураций
|
Серия |
Среднее арифметическое |
Стандартное отклонение |
Число степеней свободы |
Статистика t-критерия |
|
Серия 1 |
-0,00858 |
0,0242 |
29 |
1,9 |
|
Серия 2 |
-0,0110 |
0,0354 |
29 |
1,7 |
Таким образом, неопределенность, соответствующая конфигурации Sconfig, равна нулю (Sconfig = 0).
8.6 Вычисление неопределенности
8.6.1 Основные положения
Вычисление неопределенности зависит от того, какое значение регистрируют в отчете. В рассматриваемом случае таким значением удельного сопротивления для каждой пластины является среднее арифметическое шести (или более) краткосрочных повторений, выполненных в центре пластины в один день в одной серии.
В соответствии с моделью раздела 8
Ylkj = μ + γl + δlk + εlkj.
Значение для конкретной пластины в k-й день в i-й серии:
![]()
8.6.2 Бюджет неопределенности
Бюджет неопределенности приведен в таблице 13.
Таблица 13 - Бюджет неопределенности
|
Источник |
Тип оценки неопределенности |
Оценка дисперсии |
|
Повторяемость |
А |
S2 = 0,0008046 |
|
Отклонения, соответствующие дням |
А |
|
|
Отклонения, соответствующие сериям |
А |
|
|
Отклонения, соответствующие зонду № 2362 |
А |
|
|
Отклонения, соответствующие конфигурациям |
А |
|
8.6.3 Суммарная стандартная неопределенность
Суммарную стандартную неопределенность, включающую в себя составляющие для повторяемости, смещений, соответствующие дням, сериям и зондам, вычисляют на основе бюджета неопределенности
8.6.4 Эффективное число степеней свободы
Эффективное число степеней свободы, соответствующее uс, аппроксимируется формулой Велча-Саттервейта. Суммарная дисперсия в соответствии с 8.1
|
|
Числа степеней свободы, соответствующие этим составляющим: 44, 10, 1, и 9. Эффективное число степеней свободы согласно формуле Велча-Саттервейта:
|
|
Критическое значение для вероятности 0,95 и 17 степеней свободы равно 2, 11, и, таким образом, расширенная неопределенность
U = 2,11 uс = 0,082 Ом·см.
Приложение А
(обязательное)
Условные обозначения
|
|
- оценка смещения k-го средства измерений (k-й единицы оборудования); |
|
S2 |
- оценка дисперсии погрешности (ошибки); |
|
|
- оценка дисперсии смещения k-го средства измерений (k-й единицы оборудования); |
|
|
- оценка дисперсии, характеризующей влияние конфигурации; |
|
|
- оценка составляющей дисперсии, характеризующей влияние дней; |
|
|
- оценка составляющей дисперсии, характеризующей влияние серии; |
|
MS |
- средний квадрат отклонений; |
|
MSD |
- средний квадрат отклонений по дням для двухуровневого иерархического эксперимента; |
|
MSD(R) |
- средний квадрат отклонений для трехуровневого иерархического эксперимента; |
|
MSE |
- средний квадрат отклонений случайных ошибок; |
|
MSinh |
- средний квадрат отклонений, характеризующий неоднородность объектов испытаний; |
|
MSinst |
- средний квадрат отклонений, характеризующий оборудование; |
|
MSitem |
- средний квадрат отклонений, соответствующий объектам испытаний; |
|
MSR |
- средний квадрат отклонений, характеризующий влияние серии; |
|
SS |
- сумма квадратов отклонений; |
|
SSD(R) |
- сумма квадратов отклонений, соответствующих дням; |
|
SSE |
- сумма квадратов отклонений для случайных ошибок; |
|
SSR |
- сумма квадратов отклонений, соответствующих серии; |
|
Y |
- выходная величина, которую можно повторять; |
|
δ |
- влияющий фактор уровня 2, например день; |
|
ε |
- случайная ошибка; |
|
γ |
- влияющий фактор уровня 3, например серия; |
|
μ |
- истинное среднее (математическое ожидание) или среднее арифметическое очень большого количества измерений; |
|
v |
- число степеней свободы, соответствующее неопределенности; |
|
σ2 |
- дисперсия случайной ошибки (истинная); |
|
|
- дисперсия, соответствующая дням (истинная); |
|
|
- дисперсия, соответствующая серии (истинная). |
Примечание - Знак «^» над символом означает оценку. Например ![]() .
.
Приложение В
(справочное)
Сведения о соответствии национальных стандартов Российской Федерации ссылочным
международным стандартам
Таблица В.1
|
Обозначение ссылочного международного стандарта |
Обозначение и наименование соответствующего национального стандарта |
|
ИСО 3534-1:2006 |
ГОСТ Р 50779.10-2000 (ИСО 3534-1-93) Статистические методы. Вероятность и основы статистики. Термины и определения |
|
ИСО 3534-3:1999 |
ГОСТ Р 50779.11-2000 (ИСО 3534-2-93) Статистические методы. Статистическое управление качеством. Термины и определения |
|
ИСО 5725-1:1994 |
ГОСТ Р ИСО 5725-1-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 1. Основные положения и определения |
|
ИСО 5725-2:1994 |
ГОСТ Р ИСО 5725-2-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 2. Основной метод определения повторяемости и воспроизводимости стандартного метода измерений |
|
ИСО 5725-3:1994 |
ГОСТ Р ИСО 5725-3-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 3. Промежуточные показатели прецизионности стандартного метода измерений |
|
ИСО 5725-4:1994 |
ГОСТ Р ИСО 5725-4-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 4. Основные методы определения правильности стандартного метода измерений |
|
ИСО 5725-5:1998 |
ГОСТ Р ИСО 5725-5-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 5. Альтернативные методы определения прецизионности стандартного метода измерений |
|
ИСО 5725-6:1994 |
ГОСТ Р ИСО 5725-6-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 6. Использование значений точности на практике |
|
ИСО/ТУ 21748:2004 |
Р 50.1.060-2006 Статистические методы. Руководство по использованию оценок повторяемости, воспроизводимости и правильности при оценке неопределенности измерений |
|
ИСО Руководство 35:2000 |
* |
|
* Соответствующий национальный стандарт отсутствует. До его утверждения рекомендуется использовать перевод на русский язык данного международного стандарта. Перевод данного международного стандарта находится в Федеральном информационном фонде технических регламентов и стандартов. |
|
Библиография
|
ИСО/МЭК Руководство 98:1995 Руководство по выражению неопределенности измерений |
|
|
|
(ISO/IEC Guide 98:1995) (Guide to the expression of uncertainty in measurement (GUM)) |
|
Churchill Eisenhart. Realistic Evaluation of the
Precision and Accuracy of Instrument Calibration Systems J Research National
Bureau of Standards-C. Engineering and Instrumentation, |
|
|
Gerald J. Hahn and William Q. Meeker. Statistical
Intervals: A Guide for Practitioners, John Wiley & Sons, Inc., |
|
|
Harry Ku. Notes on the Use of Propagation of
uncertainty Formulas. J Research of National Bureau of Standards-C.
Engineering and Instrumentation, |
Ключевые слова: статистические методы, обработка данных, выборочный контроль, контрольные карты, возможности процесса, способность обнаружения, точность, правильность, прецизионность, повторяемость, воспроизводимость