|
ФЕДЕРАЛЬНОЕ
АГЕНТСТВО |
||
|
|
НАЦИОНАЛЬНЫЙ |
ГОСТ Р (ИСО 9080:2003) |
ТРУБЫ ИЗ ТЕРМОПЛАСТИЧНЫХ МАТЕРИАЛОВ
Определение
длительной гидростатической
прочности на образцах труб методом экстраполяции
ISO 9080:2003
Plastics piping and ducting
systems - Determination of the
long-term hydrostatic
strength of thermoplastics materials in pipe form by extrapolation
(MOD)
|
|
Москва |
Предисловие
Цели и принципы стандартизации в Российской Федерации установлены Федеральным законом от 27 декабря 2002 г. № 184-ФЗ «О техническом регулировании», а правила применения национальных стандартов Российской Федерации - ГОСТ Р 1.0-2004 «Стандартизация в Российской Федерации. Основные положения»
Сведения о стандарте
1 ПОДГОТОВЛЕН ОАО «Научно-исследовательский институт санитарной техники», ООО «Группа ПОЛИПЛАСТИК» при участии фирм ООО «ТЕСЕ Системе», ООО «Экструзионные машины», «HENCOINDUSTRIES N.V.», ЗАО «Упонор Рус» на основе собственного аутентичного перевода на русский язык международного стандарта, указанного в пункте 4
2 ВНЕСЕН Техническими комитетами по стандартизации ТК 465 «Строительство» и ТК 241 «Пленки, трубы, фитинги, листы и другие изделия из пластмасс»
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 15 декабря 2011 г. № 1572-ст
4 Настоящий стандарт является модифицированным по отношению к международному стандарту ИСО 9080:2003 «Пластмассовые трубы и системы трубопроводов. Определение длительной гидростатической прочности термопластичных материалов в форме труб путем экстраполяции» (ISO 9080:2003 «Plastics piping and ducting systems - Determination of the long-term hydrostatic strength of thermoplastics materials in pipe form by extrapolation») путем исключения из текста ссылок на ИСО 1167 и ИСО 3146:2000, не применяемые в Российской Федерации, и дополнения нормативными ссылками на ГОСТ 15088-83, ГОСТ 21553-76 и ГОСТ 24157-80.
Наименование настоящего стандарта изменено по отношению к наименованию международного стандарта для приведения в соответствие с ГОСТ Р 1.5-2004 (пункт 3.5)
5 ВВЕДЕН ВПЕРВЫЕ
Информация об изменениях к настоящему стандарту публикуется в ежегодно издаваемом информационном указателе «Национальные стандарты», а текст изменений и поправок - в ежемесячно издаваемых информационных указателях «Национальные стандарты». В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ежемесячно издаваемом информационном указателе «Национальные стандарты». Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет
СОДЕРЖАНИЕ
Введение
Стандартный экстраполяционный метод (СЭМ) определения длительной гидростатической прочности, приведенный в настоящем стандарте, предназначен для оценки термопластичных материалов на образцах труб до их внедрения на рынке. Данный метод не отменяет существующие методы расчета напряжений или допускаемых давлений для полимерных труб, опыт длительной эксплуатации которых является удовлетворительным.
Пригодность полимерных материалов для напорных труб определяется их длительным поведением под воздействием гидростатического напряжения с учетом ожидаемых условий эксплуатации (например, температуры), которое труба может выдержать в течение 50 лет при температуре 20 °C, если в качестве внутренней испытательной среды применяется вода, при этом внешней средой может быть вода или воздух.
В определенных случаях гидростатическую прочность необходимо определять при меньшем сроке службы или повышенных температурах, или с учетом указанных условий одновременно, при этом для оценки длительной гидростатической прочности труб может применяться метод, приведенный в настоящем стандарте. Полученный результат будет характеризовать нижний прогнозируемый предел длительной прочности, являющийся нижним доверительным пределом прогнозируемого значения напряжения, которое может вызвать разрушение материала трубы в установленные сроки при заданных температурах (предельное напряжение).
Примечание - Значение минимальной длительной прочности MRS при температуре 20 °C, как правило, основано на результатах, полученных при испытании с использованием воды в качестве внутренней и внешней испытательных сред. При этом действительными являются все результаты, используемые для проверки кривых регрессии при более высоких температурах (например, при температуре 70 °C), в том числе результаты, полученные с использованием в качестве внешней среды воздуха (например, при температуре 110 °C).
В настоящем стандарте приведена методика экстраполяции результатов испытаний при различных температурах, предусматривающая использование многофакторных линейных регрессий. Полученные результаты дают возможность определять характерные для полимерного материала расчетные значения напряжения в соответствии с методами, приведенными в стандартах на трубы конкретных видов.
Анализ многофакторной линейной регрессии основан на скорости процессов, наиболее точно описываемых моделью отношения логарифма напряжения (lg напряжения) к логарифму времени (lg времени). Для оценки прогнозируемого значения применяемой модели принято использовать ожидаемый 97,5 %-ный нижний прогнозируемый предел длительной прочности, эквивалентный нижнему доверительному пределу 95 %-ного доверительного интервала прогнозируемого значения. Данное соотношение применяют в математических расчетах с использованием статистических методов.
Метод, приведенный в настоящем стандарте, позволяет проводить экстраполяцию значений напряжения разрушения в условиях эксплуатации, отличающихся от обычных (при температуре 20 °C в течение 50 лет).
С учетом коэффициентов экстраполяции (см. 5.1.4) временной предел экстраполяции может увеличиться до 100 лет. При этом внутренняя среда, используемая для создания давления в трубе, не должна отрицательно влиять на трубу. В качестве такой среды применяют, как правило, воду.
Для расчета длительной гидростатической прочности в качестве независимой переменной, наиболее подвергающейся воздействию разброса, принято время, что позволяет проводить корректную статистическую обработку полученных результатов методом, приведенным в настоящем стандарте. При этом напряжение принято представлять как функцию времени.
Метод экстраполяции, приведенный в настоящем стандарте, позволяет:
- оценить нижний прогнозируемый предел напряжения (на уровне 97,5 %-ной вероятности), которое труба, изготовленная из конкретного материала, способна выдержать в течение 50 лет при температуре 20 °C, если в качестве испытательной среды используют воду или воздух;
- оценить нижний прогнозируемый предел напряжения (на уровне 97,5 %-ной вероятности) при разных сроках службы трубы или при разных температурах, или, в некоторых случаях, при указанных условиях одновременно.
В приведенном методе экстраполяции применяют только модели с двумя, тремя или четырьмя параметрами. Большее число параметров может увеличить погрешность результатов.
Стандартный экстраполяционный метод (СЭМ) описывает правила оценки нижнего прогнозируемого предела напряжения (с 97,5 %-ным уровнем вероятности), устанавливает наличие перегиба, который указывает на переход между разрушениями типов А и В или его отсутствие (см. приложение В).
Окончательным результатом СЭМ для конкретного материала является нижний прогнозируемый предел гидростатической прочности (с 97,5 %-ным уровнем вероятности), выраженный в единицах напряжения при заданных времени и температуре.
ГОСТ Р 54866-2011
(ИСО 9080:2003)
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
ТРУБЫ ИЗ ТЕРМОПЛАСТИЧНЫХ МАТЕРИАЛОВ
Определение
длительной гидростатической
прочности на образцах труб методом экстраполяции
Thermoplastics
pipes.
Determination of the long-term hydrostatic strength on pipe samples by
extrapolation method
Дата введения - 2013-01-01
1 Область применения
Настоящий стандарт распространяется на трубы из термопластичных материалов и устанавливает правила оценки длительной гидростатической прочности методом статистической экстраполяции.
Метод, приведенный в настоящем стандарте, применяют для всех видов термопластичных труб, применяемых при различных температурах. Метод разработан на основе статистической обработки результатов испытания труб.
Размеры образцов труб могут быть приведены в стандартах на трубы конкретного вида и должны быть включены в протокол испытаний.
2 Нормативные ссылки
В настоящем стандарте использованы нормативные ссылки на следующие стандарты:
ГОСТ Р ИСО 3126-2007 Трубопроводы из пластмасс. Пластмассовые элементы трубопровода. Определение размеров (ИСО 3126:2007, IDT)
ГОСТ Р 50825-95 (ИСО 2507:72) Трубы и детали соединительные из непластифицированного поливинилхлорида. Определение температуры размягчения по Вика (ИСО 2507:72*, MOD)
_______
* Действует ИСО 2507-1:1995.
ГОСТ 15088-83 Пластмассы. Метод определения температуры размягчения термопластов по Вика
ГОСТ 21553-76 Пластмассы. Методы определения температуры плавления
ГОСТ 24157-80 Трубы из пластмасс. Метод определения стойкости при постоянном внутреннем давлении
Примечание - При пользовании настоящим стандартом целесообразно проверить действие ссылочного стандарта в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет или по ежегодно издаваемому информационному указателю «Национальные стандарты», который опубликован по состоянию на 1 января текущего года, и по соответствующим ежемесячно издаваемым информационным указателям, опубликованным в текущем году. Если ссылочный стандарт заменен (изменен), то при пользовании настоящим стандартом следует руководствоваться заменяющим (измененным) стандартом. Если ссылочный стандарт отменен без замены, то положение, в котором дана ссылка на него, применяется в части, не затрагивающей эту ссылку.
3 Термины и определения
В настоящем стандарте применены следующие термины с соответствующими определениями:
3.1 внутреннее давление p, МПа: Сила, с которой внутренняя среда действует на стенку трубы, отнесенная к единице площади.
3.2 напряжение s, МПа: Сила, действующая на стенку трубы в кольцевом (радиальном) направлении и возникающая в результате воздействия внутреннего давления, отнесенная к единице площади.
Примечание - Напряжение, вызванное воздействием внутреннего давления, рассчитывают по упрощенной формуле
![]()
где p - внутреннее давление в трубе, МПа;
dem - средний наружный диаметр трубы, мм;
еy,min - минимальная измеренная толщина стенки трубы, мм.
3.3 температура испытания Tt, °C: Температура, при которой были определены значения разрушающего напряжения.
3.4 максимальная температура испытания Tt,max, °C: Максимальная температура, при которой были определены значения разрушающего напряжения.
3.5 рабочая температура Ts, °C: Температура, при которой предполагается эксплуатировать трубу.
3.6 время до разрушения t, ч: Время от начала нагружения до момента появления течи в трубе.
3.7 длительная гидростатическая прочность sLTHS, МПа: Величина с размерностью напряжения, характеризующая прогнозируемую среднюю прочность при температуре T и времени t.
3.8 нижний доверительный предел прогнозируемой гидростатической прочности sLPL, МПа: Величина с размерностью напряжения, представляющая собой 97,5 %-ный нижний доверительный предел прогнозируемой гидростатической прочности при температуре T и времени t.
Примечание - Обозначается как sLPL = s(T,t,0,975).
3.10 ветвь: Линия постоянного наклона на графике зависимости lg (напряжения) от lg (времени), представляющая одинаковый тип разрушения.
3.11 коэффициент экстраполяции во времени ke: Коэффициент для расчета пределов экстраполяции длительной прочности во времени.
4 Условия сбора статистических данных
4.1 Условия испытаний
Значения разрушающего напряжения в трубе определяют в соответствии с ГОСТ 24157. Образцы труб для проведения испытаний должны быть изготовлены из прямых отрезков труб.
Средний наружный диаметр и минимальную толщину стенки трубы каждого образца определяют в соответствии с ГОСТ Р ИСО 3126.
В случае разногласий испытывают образцы труб одного диаметра, выбранного из диапазона от 25 до 63 мм. Образцы должны быть изготовлены из одной партии материала и на одной и той же экструзионной линии.
4.2 Распределение уровней внутреннего давления и интервалов времени
Уровни внутреннего давления выбирают так, чтобы не менее четырех результатов было получено при времени до разрушения образца свыше 7000 ч и не менее одного - при времени до разрушения свыше 9000 ч (см. также 5.1.4). При наличии перегиба на графике (см. 3.9) должно быть собрано статистически достаточное число результатов испытаний для обеих ветвей графика для обеспечения необходимой точности расчета.
4.2.2 Наблюдениями за испытаниями при всех температурах в течение времени до разрушения менее 10 ч следует пренебречь.
4.2.3 При испытании при температуре £40 °C с временем до разрушения до 1000 ч разрушениями допускается пренебрегать при условии, что число остальных наблюдений соответствует 4.2.1. В этом случае все точки по выбранным времени и температуре должны быть отброшены.
4.2.4 Образцы, не имеющие разрушений на самом низком уровне внутреннего давления, могут быть использованы в качестве объектов наблюдений в многофакторных регрессионных расчетах и для определения наличия перегиба при условии, что они не приводят к отрицательным результатам испытания. В противном случае указанные образцы могут быть отброшены.
5 Метод экстраполяции
5.1 Сбор и анализ результатов испытаний
Примечание - Метод экстраполяции основан на линейной регрессии, правила расчета которой приведены в приложении А. Для определения наличия или отсутствия перегиба должны быть проведены испытания при одной или более температурах в течение одного года.
5.1.1 Условия получения результатов испытаний
Результаты испытаний должны быть получены с учетом требований, приведенных в разделе 4, а также следующих условий с использованием двух или более температур из ряда T1, T2, ..., Tn:
a) каждая пара соседних температур должна отличаться не менее чем на 10 °C;
b) максимальная температура испытания Tt,max не должна превышать температуру размягчения по Вика, определяемую по ГОСТ Р 50825 или ГОСТ 15088, минус значение температуры 15 °C для аморфных или преимущественно аморфных полимеров, или температуру плавления, определяемую в соответствии с ГОСТ 21553 минус значение температуры 15 °C для кристаллических или полукристаллических полимеров;
c) число результатов испытаний и их распределение по уровням внутреннего давления при каждой температуре должно соответствовать требованиям 4.2;
d) для получения оптимальной оценки нижнего доверительного предела прогнозируемой гидростатической прочности sLPL диапазон температур испытания должен быть выбран так, чтобы он включал в себя температуру эксплуатации или диапазон температур эксплуатации труб;
e) результаты, полученные при минимальных температурах испытаний, могут быть использованы для расчета прочности при температуре на 20 °C ниже минимальной температуры испытания при условии отсутствия каких-либо изменений состояния материала.
Любые разрушения вследствие присутствия в материале посторонних включений не учитывают.
5.1.2 Обнаружение перегиба и подтверждение достоверности результатов испытаний и модели
Для определения наличия перегиба применяют метод, приведенный в приложении В.
При наличии перегиба при любой конкретной температуре результаты испытаний подразделяют на две группы: принадлежащие к первой ветви и принадлежащие ко второй ветви графика зависимости логарифма напряжения от логарифма времени.
Рассчитывают многофакторную линейную регрессию в соответствии с приложением А отдельно для каждой температуры и для результатов, относящихся к первой и второй ветвям графика.
При использовании одного температурного режима проводят анализ однофакторной линейной регрессии. В этом случае коэффициент экстраполяции во времени ke (см. 5.1.4) не применяют.
Примечание - При анализе результатов, связанных с появлением перегиба, следует обратить внимание на появление разрушения вследствие деградации полимера. Эти результаты (обычно расположенные вблизи линии, характеризующей независимость времени разрушения от напряжения, и визуально узнаваемые) не учитывают при расчете ветвей разрушения.
5.1.3 Визуальное подтверждение достоверности
Для визуального подтверждения достоверности результатов испытаний анализируют график полученной линейной регрессии sLTHS и sLPL в координатах Igs/lgt.
5.1.4 Пределы экстраполяции во времени te и коэффициент экстраполяции во времени ke
Пределы экстраполяции во времени te, для которых допускается экстраполяция, определяют следующим образом.
Рассчитывают разность температур DT, °C, по формуле
DT = Tt - T, (1)
где Tt - температура испытания, при которой использование коэффициента экстраполяции во времени ke допустимо, Tt £ Tt,max, °C;
T - температура, для которой рассчитывают предел экстраполяции во времени (T ³ Ts), °C;
Tt,max - максимальная температура испытания, °C;
Ts - температура эксплуатации трубы, °C.
Коэффициент экстраполяции во времени ke как функцию от DT принимают по таблице 1.
Предел экстраполяции во времени te, ч, рассчитывают по формуле
tе = kе,max · tmax. (2)
Максимальное время испытания tmax в часах определяют как среднее логарифмическое значение из пяти самых продолжительных времен до разрушений образца, не обязательно принадлежащих одинаковому уровню напряжения, но полученных при одной температуре. Результаты испытаний образцов, не разрушившихся по истечении 4000 ч, могут быть включены в расчет многофакторной линейной регрессии, если они не ухудшают общий результат расчетов.
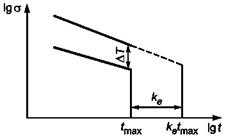
Примеры применения экстраполяции во времени представлены на рисунках 1 - 3.
Рисунок 1 -
Пределы экстраполяции во времени при отсутствии перегиба
при максимальной температуре испытания
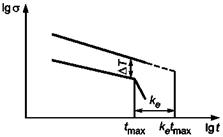
Рисунок 2 -
Пределы экстраполяции во времени при наличии перегиба только
при максимальной температуре испытания
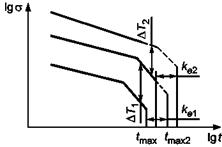
Рисунок
3 - Пределы экстраполяции во времени при наличии перегибов
при различных температурах испытания
На рисунке 1 показан пример при отсутствии перегиба при максимальной температуре испытания.
На рисунке 2 показан пример, когда перегиб был обнаружен при максимальной температуре испытания.
На рисунке 3 показан пример, когда перегиб был обнаружен при различных температурах испытания.
Значения коэффициента экстраполяции во времени ke приведены в 5.2 и 5.3.
Коэффициенты экстраполяции во времени ke для полиолефинов приведены в таблице 1.
Пределы экстраполяции во времени результатов разрушения образцов полиолефинов устанавливают с учетом экспериментально определенного срока их службы при максимальной температуре испытания и уравнения температурной зависимости Аррениуса при кажущейся энергии активации второй ветви графика для стабилизированных полиолефинов, равной 110 кДж/моль.
Таблица 1 - Коэффициенты экстраполяции ke для полиолефинов
|
Разность температур DT, °C |
Коэффициент экстраполяции во времени ke |
|
³ 10 < 15 |
2,5 |
|
³ 15 < 20 |
4 |
|
³ 20 < 25 |
6 |
|
³ 25 < 30 |
12 |
|
³ 30 < 35 |
18 |
|
³ 35 < 40 |
30 |
|
³ 40 < 50 |
50 |
|
³ 50 |
100 |
Коэффициенты экстраполяции во времени ke приведены в таблице 2.
Пределы экстраполяции во времени результатов разрушения образцов стеклообразных и аморфных полимеров на основе винилхлорида устанавливают с учетом экспериментально определенного срока их службы при максимальной температуре испытания, которая должна быть на 15 °C ниже температуры размягчения по Вика, и уравнения температурной зависимости Аррениуса при кажущейся энергии активации второй ветви графика для полимеров на основе винилхлорида, равной 178 кДж/моль.
Для модифицированных поливинилхлоридных (ПВХ) материалов коэффициенты экстраполяции во времени, приведенные в таблице 2, используют в случае, если базовым полимером модифицированного ПВХ является винилхлорид.
Таблица 2 - Коэффициенты экстраполяции ke для полимеров на основе винилхлорида
|
Разность температур DT, °C |
Коэффициент экстраполяции ke |
|
³ 5 < 10 |
2,5 |
|
³ 10 < 15 |
5 |
|
³ 15 < 20 |
10 |
|
³ 20 < 25 |
25 |
|
³ 25 < 30 |
50 |
|
³ 30 |
100 |
5.4 Коэффициенты экстраполяции во времени ke для полимеров, не указанных в 5.2 и 5.3
Коэффициенты экстраполяции во времени ke, приведенные в таблице 1, могут считаться минимальными значениями для полимеров, не указанных в настоящем стандарте.
Если экспериментально доказано, что для конкретного полимера обоснованы более высокие коэффициенты экстраполяции, то эти коэффициенты могут быть использованы вместо коэффициентов, приведенных в таблице 1.
6 Пример расчета кривых регрессии для полукристаллического полимера, подтверждение достоверности программного обеспечения
Пример расчета кривых регрессии при температурах 20 °C, 40 °C и 60 °C и пример обнаружения перегиба методами по разделу 5 приведены в приложении С.
Результаты испытаний, представленные в С.1 приложения С, приведены для проверки компьютерной программы (см. приложение Д). Если использована компьютерная программа, отличающаяся от указанной в приложении Д, то результаты вычисления по этой программе должны совпадать с результатами, полученными в соответствии с приложением С, с точностью до третьего десятичного знака.
7 Протокол испытаний
7.1 Протокол испытаний должен включать в себя:
a) ссылку на настоящий стандарт;
b) полную идентификацию образцов труб, в том числе наименование производителя труб, вид полимерного материала, код маркировки, источник поступления образцов труб;
c) размеры испытуемых образцов труб;
d) среду испытаний снаружи и внутри трубы, используемую для создания давления в образце трубы;
e) таблицу наблюдений, включающую в себя для каждого наблюдения температуру испытания, в градусах Цельсия, давление и напряжение, в мегапаскалях, время до разрушения, в часах, результат визуальной оценки типа разрушения (пластический, хрупкий или неизвестный), дату проведения испытания и др. результаты наблюдений, которые могут быть значимыми;
f) число отброшенных результатов испытаний, полученных в течение 1000 ч при соответствующих температурах и времени до разрушения для данного типа разрушения;
g) модель, используемую для оценки sLTHS и sLPL;
h) рассчитанные коэффициенты ci (см. приложение А) и их стандартные отклонения si для каждой ветви графика отдельно;
i) графическое изображение результатов испытаний, линий линейных регрессий sLTHS и sLPL;
j) сведения о программе, используемой для расчетов;
k) любые факторы, не установленные в настоящем стандарте, которые могут повлиять на результаты.
Приложение А
(обязательное)
Методы сбора и анализа результатов
А.1 Общая модель
Общая модель с четырьмя параметрами, используемая в настоящем стандарте для расчетов, описывается уравнением
где t - время до разрушения образца, ч;
T - температура, для которой рассчитывают предел экстраполяции во времени, К (°C + 273,15);
s - кольцевое напряжение в образце трубы, МПа;
c1, c2, c3, c4 - коэффициенты, рассчитываемые по результатам испытаний;
e - ошибка переменной, имеющая распределение Лапласа-Гаусса с нулевым средним значением и постоянной дисперсией (ошибки считаются независимыми).
Модель с четырьмя параметрами должна быть преобразована в модель с тремя параметрами, если уровень вероятности коэффициента c3 превышает 0,05. В этом случае c3 = 0, а уравнение (А.1) принимает вид
![]() (А.2)
(А.2)
Модель с двумя параметрами выбирают, если все результаты испытаний получены при одной температуре.
![]() (А.3)
(А.3)
Расчеты для модели с четырьмя параметрами приведены ниже. Расчеты для других моделей могут быть получены путем исключения соответствующих величин.
При проведении расчетов матриц все арифметические вычисления должны быть выполнены с двойной точностью (до 14 значащих цифр). Преобразование матриц проводят, применяя классический подход Гаусса-Джордана [1].
Применяют следующие матричные записи:
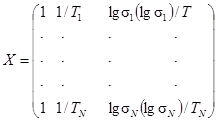
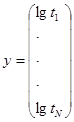
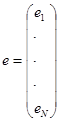 ,
,
где N - общее число наблюдений.
При c = (c1, c2, c3, c4)T, где T является оператором перестановки, модель, описываемая уравнением (А.1), может быть записана в следующем виде:
y = Xс + e.
Оценку остаточной дисперсии s2 проводят по формуле
![]() (A.4)
(A.4)
где q - число параметров в модели.
Расчет
параметра ![]() проводят методом наименьших квадратов
по формуле
проводят методом наименьших квадратов
по формуле
![]() (А.5)
(А.5)
Значение прогнозируемого напряжения по отношению к полученному времени до разрушения t и температуре T определяют по формуле
![]() (A.6)
(A.6)
Для расчета нижнего доверительного предела прогнозируемой гидростатической прочности sLPL, соответствующего времени до разрушения t и температуре T, проводят преобразование, используя соотношение
![]() (A.7)
(A.7)
где tSt - t - значение критерия Стьюдента, соответствующее уровню вероятности 0,975 и числу степеней свободы N - 4;
x - вектор [1, 1/T, lgs, (lgs)/T].
Результатом преобразования является уравнение
![]()
где ![]()
![]()
![]()
Kij - элемент матрицы (ХТХ)-1.
Значение нижнего доверительного предела прогнозируемой гидростатической прочности sLPL может быть рассчитано по формуле
sLPL = 10exp(lgsLPL). (A.8)
А.2 Упрощенные модели
В качестве упрощенных моделей могут быть использованы модели с тремя параметрами (c3 = 0) и двумя параметрами (c2 = 0, c4 = 0).
Модель с тремя параметрами имеет вид:
lgs = (lgt - c1 - c2/Т) Т/c4 с учетом параметров:
![]()
![]()
![]()
![]() соответствует N - 3 степеням
свободы.
соответствует N - 3 степеням
свободы.
Модель с двумя параметрами имеет вид:
lgs = (lgt - c1)/c3 с учетом параметров:
![]()
![]()
![]()
![]() соответствует N - 2 степеням
свободы.
соответствует N - 2 степеням
свободы.
А.3 Расчет sLTHS и sLPL с учетом перегиба
В соответствии с приложением В механизмы двух типов разрушений могут действовать каждый в своем диапазоне температур и времени до разрушения. Два набора результатов испытаний, соответствующих каждому типу разрушения, должны быть представительными независимо от модели. Для проведения расчетов экспериментальные данные делят на две группы, в каждой из которых действующим считают один из типов разрушения.
Значения sLTHS и sLPL в каждой группе могут быть рассчитаны по общей методике, приведенной в настоящем приложении, при условии достаточности приведенных данных и их удовлетворительного распределения в температурном диапазоне (см. 4.2 и 5.1.1).
Для обнаружения перегиба при каждой температуре применяют метод, приведенный в приложении В, в соответствии с которым результаты испытаний разделяют на две группы и оценивают соответствие примененной модели полученным результатам по общей методике, приведенной в настоящем приложении.
А.4 Оценка соответствия
Для оценки соответствия принятой модели экспериментальным данным применяют следующий статистический критерий F:
![]() (A.9)
(A.9)
где SSe - сумма квадратов разности между каждым отдельным экспериментальным результатом и их соответствующим средним значением для повторяющихся экспериментальных условий, при которых были получены результаты (метод расчета не зависит от примененной модели);
SSH - сумма квадратов разности между каждым отдельным экспериментальным результатом и значением, прогнозируемым с помощью использованной модели для экспериментальных условий, при которых получены результаты;
ve - число степеней свободы для SSe (число результатов испытаний минус число различных экспериментальных условий);
vH - число степеней свободы для SSH (число результатов испытаний минус число параметров в использованной модели).
Если согласно гипотезе использованная модель соответствия является корректной, то статистический критерий F подчиняется F-распределению с vH - ve степенями свободы для числителя и ve степенью свободы для знаменателя.
Используя F-распределение, можно определить вероятность того, что значение статистического критерия F будет превышать значение, рассчитанное по формуле (А.9). Данную вероятность сравнивают со значимым пределом 0,05. Если указанный предел превышен, то гипотезу о том, что модель является корректной, принимают. Если предел не превышен, гипотезу отклоняют.
Примечание - Приведенную оценку принятой модели принимают как указание на то, что соответствие модели имеет место.
Приведенный ниже пример расчета критерия соответствия результатов испытаний при температуре 20 °C, приведенных в таблице С.1, предполагает использование модели с двумя параметрами:
2SSe = 2,37778; ve = 31 - 15 = 16.
SSH = 5,98424; vH = 31 - 2 = 29.
Значение критерия F (13; 16) равно 1,86675.
Вероятность того, что F-распределение с конкретным числом степеней свободы превышает указанное значение, равна:
Pr[F(13; 16) > 1,86675] = 0,1183.
При значимом пределе, установленном на уровне 0,05, модель принимают, так как вероятность превышает установленный уровень.
Приложение В
(обязательное)
Метод автоматического обнаружения перегиба
B.1 Сущность метода
Метод, приведенный в настоящем приложении, позволяет обнаруживать любой перегиб посредством вычислений, выполненных для каждой отдельной температуры испытания.
Предполагается, что для конкретной температуры и типа разрушения между логарифмом lg гидростатического напряжения, которому подвергнут образец трубы, и логарифмом lg времени до разрушения образцов трубы существует линейная зависимость и измерения времени до разрушения подвержены случайной погрешности. При этом тип разрушения зависит от значения гидростатического напряжения: разрушение типа В - при напряжениях ниже значения перегиба, типа А - при напряжениях выше этого значения.
B.2 Процедура обнаружения перегиба
Модель, отражающая сущность метода и принимающая во внимание типы разрушения, имеет вид
lgt = c1 + c3 lgs + c1i + c3i lgs + e,
при этом принимают, что c11 + c12 = c31 + c32 = 0 (для устранения сингулярности - непредсказуемого изменения модели),
где e - ошибка переменной.
Примечание - Ошибки, предположительно, должны быть независимы и нормально распределены с нулевым средним значением и постоянной дисперсией.
В приведенной выше модели параметры c1i и c3i отражают влияние качественной переменной «тип разрушения»: для разрушений типа Аi = 1, для разрушений типа Вi = 2.
Приведенное ниже соотношение должно гарантировать, что перегиб отделяет два диапазона напряжения, соответствующие двум типам разрушения, при этом время до разрушения не зависит от типа разрушения
c1i + c3i · lgsk = 0,
где sk - напряжение, соответствующее перегибу.
С учетом данного соотношения, в котором параметр c1i - может быть исключен, модель принимает вид
lgt = c1 + c3 lgs + c3i (lgs - lgsk) + е при c31 + c32 = 0.
Для
практической проверки соответствия выбранной модели полученным результатам
анализируют напряжение sk по
экспериментальному диапазону значений напряжения и вычисляют остаточную
дисперсию ![]() для
каждой соответствующей линейной зависимости. Минимальное значение остаточной
дисперсии
для
каждой соответствующей линейной зависимости. Минимальное значение остаточной
дисперсии ![]() указывает
на лучшее соответствие и, следовательно, дает оптимальное значение напряжения sk.
указывает
на лучшее соответствие и, следовательно, дает оптимальное значение напряжения sk.
Для
сравнения остаточной дисперсии ![]() , соответствующей модели с перегибом, с
остаточной дисперсией s2,
соответствующей модели без перегиба, определяют статистический критерий Фишера F
, соответствующей модели с перегибом, с
остаточной дисперсией s2,
соответствующей модели без перегиба, определяют статистический критерий Фишера F
![]()
Статистический критерий Фишера F согласно гипотезе о модели без перегиба имеет F-распределение со степенями свободы N - 2 для числителя и степенями свободы N - 4 для знаменателя, где N - число измерений.
Гипотеза о том, что перегиб отсутствует, принята с уровнем вероятности 5 %, если вероятность, связанная с расчетным значением F, более значимого уровня, равного 0,05. В противном случае гипотеза отклоняется, а присутствие перегиба считают принятым.
Приложение С
(справочное)
Применение СЭМ к результатам определения длительной прочности
Результаты испытаний образцов труб из полукристаллического полимера при температурах 20 °C, 40 °C и 60 °C приведены в таблицах С.1 - С.3.
Таблица С.1 - Результаты испытаний при температуре 20 °C
|
Напряжение, МПа |
Время, ч |
Температура, °C |
Напряжение, МПа |
Время, ч |
|
|
20 |
16,0 |
11 |
20 |
13,7 |
536 |
|
20 |
15,0 |
58 |
20 |
13,6 |
680 |
|
20 |
15,0 |
44 |
20 |
13,5 |
411 |
|
20 |
14,9 |
21 |
20 |
13,5 |
412 |
|
20 |
14,5 |
25 |
20 |
13,5 |
3368 |
|
20 |
14,5 |
24 |
20 |
13,5 |
865 |
|
20 |
14,3 |
46 |
20 |
13,5 |
946 |
|
20 |
14,1 |
11 |
20 |
13,5 |
4524 |
|
20 |
14,0 |
201 |
20 |
13,4 |
122 |
|
20 |
14,0 |
260 |
20 |
13,4 |
5137 |
|
20 |
14,0 |
201 |
20 |
13,3 |
1112 |
|
20 |
13,9 |
13 |
20 |
13,3 |
2108 |
|
20 |
13,7 |
392 |
20 |
13,2 |
1651 |
|
20 |
13,7 |
440 |
20 |
13,2 |
1760 |
|
20 |
13,7 |
512 |
20 |
12,8 |
837 |
|
20 |
13,7 |
464 |
Таблица С.2 - Результаты испытаний при температуре 40 °C
|
Напряжение, МПа |
Время, ч |
Температура, °C |
Напряжение, МПа |
Время, ч |
|
|
40 |
11,1 |
10 |
40 |
10,0 |
2076 |
|
40 |
11,2 |
11 |
40 |
10,0 |
1698 |
|
40 |
11,5 |
20 |
40 |
9,5 |
1238 |
|
40 |
11,5 |
32 |
40 |
9,5 |
1790 |
|
40 |
11,5 |
35 |
40 |
9,5 |
2165 |
|
40 |
11,5 |
83 |
40 |
9,5 |
7823 |
|
40 |
11,2 |
240 |
40 |
9,0 |
4128 |
|
40 |
11,2 |
282 |
40 |
9,0 |
4448 |
|
40 |
11,0 |
1912 |
40 |
8,5 |
7357 |
|
40 |
11,0 |
1856 |
40 |
8,5 |
5448 |
|
40 |
11,0 |
1688 |
40 |
8,0 |
7233 |
|
40 |
11,0 |
1114 |
40 |
8,0 |
5959 |
|
40 |
10,8 |
54 |
40 |
8,0 |
12081 |
|
40 |
10,5 |
5686 |
40 |
7,5 |
16920 |
|
40 |
10,5 |
921 |
40 |
7,5 |
12888 |
|
40 |
10,5 |
1145 |
40 |
7,5 |
10578 |
|
40 |
10,5 |
2445 |
40 |
6,5 |
12912 |
|
40 |
10,0 |
5448 |
40 |
6,0 |
11606 |
|
40 |
10,0 |
3488 |
|||
|
40 |
10,0 |
1488 |
Таблица С.3 - Результаты испытаний при температуре 60 °C
|
Напряжение, МПа |
Время, ч |
Температура, °C |
Напряжение, МПа |
Время, ч |
|
|
60 |
9,6 |
10 |
60 |
7,5 |
351 |
|
60 |
9,5 |
13 |
60 |
7,0 |
734 |
|
60 |
9,5 |
32 |
60 |
7,0 |
901 |
|
60 |
9,5 |
34 |
60 |
7,0 |
1071 |
|
60 |
9,5 |
114 |
60 |
7,0 |
1513 |
|
60 |
9,5 |
195 |
60 |
6,5 |
1042 |
|
60 |
9,2 |
151 |
60 |
6,5 |
538 |
|
60 |
9,0 |
242 |
60 |
6,0 |
4090 |
|
60 |
9,0 |
476 |
60 |
6,0 |
839 |
|
60 |
9,0 |
205 |
60 |
6,0 |
800 |
|
60 |
9,0 |
153 |
60 |
5,5 |
339 |
|
60 |
9,0 |
288 |
60 |
5,5 |
2146 |
|
60 |
8,9 |
191 |
60 |
5,5 |
2048 |
|
60 |
8,5 |
331 |
60 |
5,5 |
2856 |
|
60 |
8,5 |
296 |
60 |
5,0 |
1997 |
|
60 |
8,5 |
249 |
60 |
5,0 |
1647 |
|
60 |
8,5 |
321 |
60 |
5,0 |
1527 |
|
60 |
8,5 |
344 |
60 |
5,0 |
2305 |
|
60 |
8,5 |
423 |
60 |
5,0 |
2866 |
|
60 |
8,5 |
686 |
60 |
4,0 |
6345 |
|
60 |
8,5 |
513 |
60 |
3,5 |
15911 |
|
60 |
8,5 |
585 |
60 |
3,4 |
6841 |
|
60 |
8,5 |
719 |
60 |
3,4 |
8232 |
|
60 |
7,5 |
423 |
60 |
2,9 |
15090 |
|
60 |
7,5 |
590 |
|||
|
60 |
7,5 |
439 |
|||
|
60 |
7,5 |
519 |
С.2 Автоматическое обнаружение перегиба
Для автоматического обнаружения перегиба в качестве примера использованы результаты испытаний при температуре 40 °C, приведенные в таблице С.2.
Предполагается, что перегиб отсутствует и результаты испытаний описываются прямой линией, проходящей через все точки. Результирующая дисперсия равна 0,4091 с 36 степенями свободы.
Затем предполагают, что перегиб имеет место, и определяют его положение, анализируя 50 значений напряжения, равномерно распределенных в экспериментальном диапазоне логарифма напряжения. Значение, соответствующее наименьшей результирующей дисперсии соответствия (принятая модель использует две прямые линии), дает точку перегиба с напряжением 10,6 МПа и временем 1927 ч. В этом случае результирующая дисперсия равна 0,227 с 34 степенями свободы.
Статистический критерий Фишера F, используемый для проверки наличия перегиба, равен 0,4091/0,227 = 1802. Вероятность, что статистический критерий Фишера с 36 и 34 степенями свободы превышает 1,802, равна 0,0438. Так как 0,0438 < 0,05, то принимают решение о наличии перегиба.
Классификация типов разрушения приведена в таблице С.4.
Таблица С.4 - Классификация типов разрушения
|
Температура, °С |
Напряжение, МПа |
Время, ч |
Тип разрушения |
Температура, °С |
Напряжение, МПа |
Время, ч |
Тип разрушения |
|
40 |
11,1 |
10 |
А |
40 |
11,5 |
35 |
А |
|
40 |
11,2 |
11 |
А |
40 |
10,8 |
54 |
А |
|
40 |
11,5 |
20 |
А |
40 |
11,5 |
83 |
А |
|
40 |
11,5 |
32 |
А |
40 |
11,2 |
240 |
А |
|
40 |
11,2 |
282 |
А |
40 |
9,5 |
1790 |
В |
|
40 |
11,0 |
1688 |
А |
40 |
9,5 |
2165 |
В |
|
40 |
11,0 |
1114 |
А |
40 |
9,5 |
7823 |
В |
|
40 |
11,0 |
1912 |
А |
40 |
9,5 |
4128 |
В |
|
40 |
11,0 |
1856 |
А |
40 |
9,0 |
4448 |
В |
|
40 |
10,5 |
921 |
В |
40 |
8,5 |
7357 |
В |
|
40 |
10,0 |
1488 |
В |
40 |
8,5 |
5448 |
В |
|
40 |
10,0 |
1698 |
В |
40 |
8,0 |
7233 |
В |
|
40 |
9,5 |
1238 |
В |
40 |
8,0 |
5959 |
В |
|
40 |
10,5 |
1145 |
В |
40 |
8,0 |
12081 |
В |
|
40 |
10,5 |
5686 |
В |
40 |
7,5 |
16920 |
В |
|
40 |
10,5 |
2445 |
В |
40 |
7,5 |
12888 |
В |
|
40 |
10,0 |
5448 |
В |
40 |
7,5 |
10578 |
В |
|
40 |
10,0 |
3488 |
В |
40 |
6,5 |
12912 |
В |
|
40 |
10,0 |
2076 |
В |
40 |
6,0 |
11606 |
В |
Примечание - Приведенный пример автоматического обнаружения перегиба иллюстрирует используемый метод. Для получения данного результата могут быть использованы различные программы расчета.
С.3 Пример расчета уравнения линейной регрессии длительной прочности
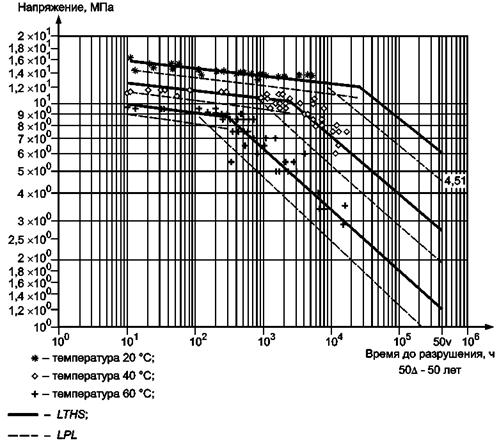
С.3.1 Графическая оценка результатов испытания (см. рисунок С.1).
Рисунок С.1 - Графическое представление результатов анализа СЭМ для полукристаллического полимера
С.3.1.1 Используемая модель
lgt = c1 + c2/Т + c4(lgs)/T + e.
С.3.1.2 Разрушение типа А
Результирующая дисперсия 0,306061.
Число результатов испытаний 50.
Число параметров 3.
Число степеней свободы 47.
Оценка параметров для разрушения типа А приведена в таблице С.5.
Таблица С.5 - Оценка параметров для разрушения типа А
|
Значение |
Стандартная ошибка |
t-критерий |
Pr (> |t|) |
|
|
c1 |
-42,014 |
+6,048 |
-6,947 |
0,000 |
|
c2 |
+23184,326 |
+3290,992 |
+7,045 |
0,000 |
|
c4 |
-8892,575 |
+1361,190 |
-6,533 |
0,000 |
Оценка пригодности модели: Pr[F(19; 28) > 2,981] = 0,004.
С.3.1.3 Разрушение типа В
Результирующая дисперсия 0,048413.
Число результатов испытаний 70.
Число параметров 3.
Число степеней свободы 67.
Оценка параметров для разрушения типа В приведена в таблице С.6.
Таблица С.6 - Оценка параметров для разрушения типа В
|
Значение |
Стандартная ошибка |
t-значение |
Pr(> |t|) |
|
|
c1 |
-15,775 |
+1,010 |
-15,619 |
0,000 |
|
c2 |
+7228,155 |
+366,250 |
+19,736 |
0,000 |
|
c4 |
-1213,615 |
+76,868 |
-15,788 |
0,000 |
Оценка пригодности модели: Pr[F(20; 47) > 0,751] = 0,753.
С.3.2 Прогноз
С.3.2.1 Общие положения
Прогнозируемые значения длительной прочности приведены в таблицах С.7 - С.10.
Пределы экстраполяции приведены в таблицах С.11 и С.12.
С.3.2.2 Разрушения типа А
Таблица С.7 - Прогнозируемые значения длительной прочности для разрушений типа А
|
Время, ч |
||||||
|
1 |
10 |
100 |
1000 |
10000 |
100000 |
|
|
sLTHS, МПа |
||||||
|
20 |
16,678 |
15,458 |
14,328 |
13,281 |
12,310 |
В |
|
40 |
13,416 |
12,372 |
11,408 |
10,519 |
В |
В |
|
60 |
10,793 |
9,901 |
9,083 |
В |
В |
В |
|
sLPL - доверительный уровень (односторонний) = 0,975, МПа |
||||||
|
20 |
15,229 |
14,183 |
13,132 |
12,074 |
11,024 |
В |
|
40 |
12,209 |
11,288 |
10,365 |
9,444 |
В |
В |
|
60 |
9,748 |
8,942 |
8,140 |
В |
В |
В |
Таблица С.8 - Прогнозируемые значения длительной прочности для разрушений типа А
|
Температура, °C |
Время, ч |
|||
|
0,5 |
1 |
10 |
50 |
|
|
sLTHS, МПа |
||||
|
20 |
12,650 |
12,364 |
В |
В |
|
40 |
В |
В |
В |
В |
|
60 |
В |
В |
В |
В |
|
sLPL - доверительный уровень (односторонний) = 0,975 МПа |
||||
|
20 |
11,398 |
11,084 |
В |
В |
|
40 |
В |
В |
В |
В |
|
60 |
В |
В |
В |
В |
С.3.2.3 Разрушения типа В
Таблица С.9 - Прогнозируемые значения длительной прочности для разрушений типа В
|
Температура, °C |
Время, ч |
|||||
|
1 |
10 |
100 |
1000 |
10000 |
100000 |
|
|
sLTHS, МПа |
||||||
|
20 |
А |
А |
А |
А |
А |
8,661 |
|
40 |
А |
А |
А |
А |
7,132 |
3,937 |
|
60 |
А |
А |
А |
6,336 |
3,368 |
1,790 |
|
sLPL - доверительный уровень (односторонний) = 0,975, МПа |
||||||
|
20 |
А |
А |
А |
А |
А |
6,550 |
|
40 |
А |
А |
А |
А |
5,427 |
2,914 |
|
60 |
А |
А |
А |
4,772 |
2,478 |
1,261 |
Таблица C.10 - Прогнозируемые значения длительной прочности для разрушений типа В
|
Время, ч |
||||
|
0,5 |
1 |
10 |
50 |
|
|
sLTHS, МПа |
||||
|
20 |
А |
А |
8,942 |
6,062 |
|
40 |
8,825 |
7,380 |
4,074 |
2,689 |
|
60 |
4,224 |
3,492 |
1,856 |
1,193 |
|
sLPL - доверительный уровень (односторонний) = 0,975 МПа |
||||
|
20 |
А |
А |
6,770 |
4,510 |
|
40 |
6,748 |
5,621 |
3,022 |
1,937 |
|
60 |
3,142 |
2,575 |
1,312 |
0,811 |
С.3.2.4 Пределы экстраполяции
Таблица С.11 - Пределы экстраполяции для Tt = 40 °C, tmax = 13160,5 ч
|
T, °C |
DT, °C |
ke |
te, ч |
te, лет |
|
20 |
20 |
6 |
78963 |
9,01 |
Таблица С.12 - Пределы экстраполяции для Tt = 60 °C, tmax = 9698,1 ч
|
T, °C |
DT, °C |
ke |
te, ч |
te, лет |
|
20 |
20 |
50 |
484907 |
55,35 |
|
40 |
20 |
6 |
58189 |
6,64 |
С.3.3 Точки перегибов
Параметры точек перегибов приведены в таблице С.13.
Таблица С.13 - Параметры точек перегиба
|
Напряжение, МПа |
Время, ч |
|
|
20 |
11,92 |
26664 |
|
40 |
10,18 |
2515 |
|
60 |
8,70 |
315 |
Библиография
[1] RALSTON A., and WILF H.S.: Mathematical Methods for Digital Computers, Volume 1, John Wiley & Sons, 1967
|
Ключевые слова: трубы из термопластов, термопластичные материалы, метод оценки длительного гидростатического напряжения, статистическая экстраполяция, коэффициент экстраполяции во времени, разрушения типов A и B |