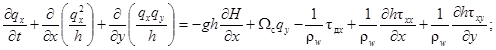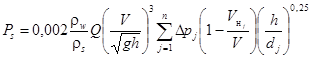РОССИЙСКОЕ АКЦИОНЕРНОЕ ОБЩЕСТВО ЭНЕРГЕТИКИ
И ЭЛЕКТРИФИКАЦИИ «ЕЭС РОССИИ»
РЕКОМЕНДАЦИИ
ПО ПРОГНОЗУ ТРАНСФОРМАЦИИ РУСЛА
В НИЖНИХ БЬЕФАХ ГИДРОУЗЛОВ
СО 34.21.204-2005
ОАО «ВНИИГ им. Б.Е. Веденеева»
Санкт-Петербург
2006
Разработано Открытым акционерным обществом «Всероссийский научно-исследовательский институт гидротехники имени Б.Е. Веденеева» (ОАО «ВНИИГ им. Б.Е. Веденеева»)
Исполнители А.Б. ВЕКСЛЕР, В.М. ДОНЕНБЕРГ (ВНИИГ)
Согласовано с филиалом ОАО «Инженерный центр ЕЭС» «Институт Гидропроект» 21.12.2004 г.
Главный инженер С.П. ПАРЕМУД
Утверждено Бизнес единица «Гидрогенерация» РАО «ЕЭС России» 02.02.2005
Заместитель Управляющего директора P.M. ХАЗИАХМЕТОВ
Срок первой проверки СО - 2012 г.
Периодичность проверки - один раз в 5 лет.
Ключевые слова: речные гидротехнические сооружения; нижний бьеф; русловой процесс; трансформация русла; наносы; транспортирующая способность; размывающая способность; расход наносов; связь расходов и уровней воды; понижение уровней; методы расчета.
|
Рекомендации |
СО 34.21.204-2005 Вводится взамен |
Дата введения 2007.01.01
ПРЕДИСЛОВИЕ
Строительство и эксплуатация гидротехнических сооружений (ГТС) оказывает существенное воздействие на окружающую среду. Характерной особенностью подпорных ГТС является создание водохранилищ и регулирование ими стока реки в нижнем бьефе. В результате аккумуляции водохранилищем твердого стока в нижний бьеф ГТС поступает осветленный поток. Это наряду с регулированием водного режима является основной причиной изменений в системе водный поток - русло, происходящих в нижнем бьефе после возведения на реке подпорных гидроузлов, в том числе и гидроузлов энергетического назначения. Результатом этих изменений является трансформация русла нижнего бьефа, выражающаяся в изменении морфометрических характеристик реки и связи расходов и уровней воды в ней по сравнению с существовавшими до строительства ГТС. Процесс трансформирования русла в отличие от обратимых, как правило, русловых переформирований незарегулированных водотоков, имеет необратимый характер и охватывает с течением времени все большие по протяженности участки реки. Прогнозирование этого процесса необходимо для учета возможных изменений в условиях эксплуатации не только самого гидроузла, являющегося первопричиной трансформации русла, но и различных инженерных сооружений, расположенных в русле и на берегах реки и зависящих от ее водного и руслового режимов.
Первые разработки методов прогноза трансформации русла при гидротехническом строительстве появились в нашей стране в предвоенные годы, но наибольшее количество разработок было сделано в 50 - 70 гг. в связи с бурным развитием в СССР строительства гидроэлектростанций и уже проявившимися последствиями первых лет их эксплуатации. В это время происходило накопление первых натурных данных, свидетельствующих об особенностях развития процесса трансформации русла, и первоначальное их обобщение. Были предложены методы расчета трансформации русла в нижних бьефах гидроузлов, различающиеся либо составом допущений, либо исходными предпосылками, определяющими точность и степень обоснованности метода. Наибольшее распространение в проектной практике получили методы, разработанные К.И. Российским и И.А. Кузьминым в институте «Гидропроект» и И.И. Леви во ВНИИГ им. Б.Е. Веденеева и ЛПИ. В то же время во многих проектных и исследовательских организациях часто использовались свои методы и приемы расчета русловых переформирований в нижних бьефах. В 1981 г. во ВНИИГ им. Б.Е. Веденеева были составлены Рекомендации по расчету трансформации русла в нижних бьефах гидроузлов: П 95-81/ВНИИГ. Этот документ явился первой нормативно-методической разработкой по данному вопросу. В нем были обобщены те из имевшихся предложений в этой области, которые представлялись наиболее обоснованными для использования в практике проектирования и научных исследований. Естественно, что Рекомендации 1981 г. не могли отразить в полной мере состояние разработки проблемы русловых переформирований в нижних бьефах, тем более, что среди исследователей не было единого мнения по целому ряду положений, определяющих этот сложный и многофакторный процесс. Поэтому основу указанных Рекомендаций составили апробированные на тот момент методы и способы назначения и вычисления параметров, необходимых на различных этапах расчета трансформации русла, без использования предложений, находившихся на стадии разработки и исследований. Этим, в частности, объяснялось то, что рассматривалась лишь одномерная расчетная модель руслового потока, основанная на представлениях классической гидравлики.
За прошедшие годы получены новые результаты в изучении руслового процесса в зарегулированных водотоках, произошел существенный прогресс в развитии численных методов расчета. Многие приближенные приемы и оценки, использовавшиеся в конце 70-х годов прошлого века, сегодня устарели и могут быть заменены более точными, совершенными. Изменилась форма представления результатов расчета и составляемого на их основе прогноза развития этого явления.
В настоящей переработанной версии Рекомендаций приведено обобщение современных представлений о процессе трансформации русла рек в нижних бьефах гидроузлов и даны рекомендации по использованию современных методов при расчете переформирования русла и изменения уровенного режима в нижнем бьефе гидроузлов в процессе их эксплуатации. Повышение точности прогноза этих явлений необходимо для обеспечения надежности и безопасности работы гидротехнических сооружений.
Использование Рекомендаций призвано обеспечить научную обоснованность учета последствий трансформации русла, в частности изменения уровней воды в нижнем бьефе, при проектировании энергогасящих устройств водопропускных сооружений гидроузлов, разработке рациональных режимов работы сооружений, анализе русловых процессов в нижних бьефах действующих гидроузлов и разработке инженерных мероприятий по снижению негативного влияния этих процессов на условия эксплуатации и безопасность объекта, а также на окружающую среду.
При этом вопросы местных деформаций за водопропускными сооружениями гидроузлов в настоящие Рекомендации не входят, им посвящены другие нормативно-методические разработки, учитывающие специфику процессов, в значительной мере связанных с избыточной турбулизацией потока и неоднородностью его структуры, обусловленной типом и условиями работы водопропускных сооружений.
Документ предназначен для использования проектными и научно-исследовательскими организациями, деятельность которых связана с проектированием, строительством и эксплуатацией речных гидроузлов.
Рекомендации подготовлены ведущим научн. сотр. А.Б. Векслером и ст. научн. сотр. В.М. Доненбергом. Текст главы 7 составлен с использованием материалов доктора физ.-мат. наук В.И. Климовича и канд. техн. наук В.А. Прокофьева.
В работе по составлению Рекомендаций принимали участие канд. техн. наук В.Л. Мануйлов, инженеры Н.Н. Коротков, Л.В. Рейнгард, Д.В. Богачева, техник Е.И. Рыбина.
При подготовке окончательной редакции Рекомендаций учтены многие замечания и предложения, содержавшиеся в отзывах на I редакцию, канд. техн. наук А.Н. Жиркевича, канд. техн. наук К.Н. Бестужевой и инж. Н.Г. Плешаковой (Институт Гидропроект); канд. физ.-мат. наук В.В. Беликова, доктора техн. наук А.М. Прудовского и инж. В.П. Середавкина (НИИЭС); проф., доктора техн. наук Б.Ф. Снищенко и канд. техн. наук Г.Г. Месерлянса (ГГИ); проф., доктора техн. наук В.К. Дебольского и канд. геогр. наук А.В. Котлякова (ИВП РАН); проф., доктора геогр. наук Р.С. Чалова, доктора геогр. наук К.М. Берковича и канд. геогр. наук Л.В. Злотиной (МГУ им. М.В. Ломоносова), а также соображения по отдельным вопросам, высказанные при рассмотрении Рекомендаций комиссией Ученого совета ВНИИГ проф., докторами техн. наук Л.В. Мошковым и В.Г. Пантелеевым (ВНИИГ им. Б.Е. Веденеева) и канд. техн. наук З.Д. Копалиани (ГГИ).
1. ОБЩИЕ ПОЛОЖЕНИЯ
Назначение и область применения
1.1. Рекомендации предназначены для использования при выполнении расчетов и прогноза трансформации русел рек в нижних бьефах проектируемых и строящихся речных гидроузлов, а также анализе направленности руслового процесса в нижних бьефах эксплуатируемых гидроузлов и оценке его влияния на окружающую среду, прогнозе его дальнейшего развития и обосновании мероприятий по нейтрализации или смягчению негативных последствий руслового процесса для окружающей среды (в том числе и для инженерных сооружений), если такие последствия обнаруживаются или прогнозируются.
1.2. Изменение естественного режима реки при возведении подпорных речных гидроузлов выражается главным образом во внутригодовом, а иногда и многолетнем перераспределении жидкого стока, частичной или полной задержке твердого стока водохранилищем и в значительных внутри-суточных колебаниях расходов и уровней воды при осуществлении регулирования мощности ГЭС (в тех случаях, когда в состав гидроузла входит гидроэлектростанция). При комплексном использовании водохранилища и отъеме из него части жидкого стока для мелиорации, переброски стока в бассейны других рек и других целей происходит общее уменьшение жидкого стока в нижнем бьефе гидроузла, а в случае переброски стока из бассейнов других рек в рассматриваемой реке происходит общее увеличение жидкого стока, что также отражается на гидрологическом режиме реки.
1.3. Изменение гидрологического режима является причиной изменения руслового процесса в нижнем бьефе гидроузла. В естественных условиях на реке преобладают обратимые деформации русла, обусловленные сезонными колебаниями стока воды и транзитным транспортом наносов, поступающих с площади водосбора. После возведения гидроузла наносы, поступавшие с площади водосбора, ограниченной створом сооружений, частично или полностью задерживаются водохранилищем, и участок реки, примыкающий к гидроузлу со стороны нижнего бьефа, превращается в зону питания наносами нижерасположенной части реки. При этом в русле начинают развиваться необратимые деформации, в которых преобладает общий размыв. На такую направленность руслового процесса накладывается влияние изменения водного режима. Обратимые деформации, вызванные движением донных форм, регулированием стока и другими факторами, развиваются на фоне основных необратимых процессов. Изменения в характере руслового процесса начинаются в период строительства гидроузла при стеснении русла перемычками и охватывают близлежащий к створу сооружений участок. В дальнейшем в период временной, а затем и постоянной эксплуатации гидроузла влияние его распространяется вниз по течению, внося изменения в естественный ход руслового процесса и трансформируя русло реки.
1.4. Трансформация русла реки в нижнем бьефе происходит под влиянием изменившихся условий течения и транспорта наносов при зарегулировании стока реки водохранилищем и обусловлена изменением макроструктуры потока, его средней скорости, глубины и сопротивлений русла.
Местные деформации русла в нижнем бьефе гидроузлов определяются главным образом избыточной турбулизацией сбросного потока, неоднородностью его структуры и условиями работы водопропускных сооружений. Влияние этих факторов ограничивается сравнительно небольшим расстоянием по длине нижнего бьефа - обычно не более 3 - 5 размеров ширин водопропускного фронта, причем наиболее заметно оно на непосредственно примыкающем к водопропускным сооружениям коротком участке, где происходит перестройка потока и его кинематика приближается к кинематике руслового потока [27]. Существенное влияние на развитие местных переформирований (главным образом размывов) оказывают стесненные условия пропуска расходов воды в период строительства сооружения, а позже - оставленные в русле неразобранные фрагменты перемычек и других строительных конструкций. Прогноз развития местных переформирований под влиянием перечисленных факторов требует иного подхода, чем прогноз трансформации русла - процесса, распространяющегося на значительную длину и практически не зависящего от частностей, которые приводят к деформациям русла, имеющим локальный характер. Поэтому прогноз местных деформаций русла является предметом рассмотрения других научно-методических документов и в настоящих Рекомендациях не рассматривается.
Сравнительно малая протяженность зоны местных деформаций русла и ее непосредственное примыкание к сооружениям гидроузла являются причиной того, что эти деформации не могут вызвать ощутимого понижения уровней, но нередко являются причиной временного подпора, обусловленного отложением продуктов местного размыва.
Все другие изменения естественной (бытовой) связи расходов и уровней воды в нижнем бьефе происходят вследствие трансформации русла, распространяющейся на значительную длину нижнего бьефа, и являются интегральным выражением этого процесса.
1.5. При проектировании гидроузла возможные изменения связи расходов и уровней нижнего бьефа в процессе эксплуатации должны быть учтены:
при расчете общей устойчивости сооружений гидроузла;
при расчете фильтрационного режима сооружений, главным образом грунтовых;
при назначении положения рабочих колес турбин;
при назначении формы сопряжения бьефов и мероприятий по креплению нижнего бьефа (водобой, рисберма, гасители и т.п.), а также определении характерных размеров участка местного размыва неукрепленного русла;
при установлении отметок порогов судопропускных сооружений.
1.6. При проектировании сооружений и мероприятий в нижних бьефах гидроузлов трансформация русла должна учитываться:
при обеспечении нормированных глубин водного транспорта и расположении причальных, ремонтных и других сооружений;
при обеспечении командных уровней и незаносимости водозаборов;
при обеспечении незаносимости и устойчивости при подмыве водовыпусков промышленных предприятий;
при обеспечении устойчивости опор инженерных сооружений, расположенных в русле реки и на ее берегах (мостовые переходы, линии электропередач и т.п.);
при обеспечении устойчивости разного рода трубопроводов, проложенных через реку или на ее берегах;
при изменениях уровня грунтовых вод (положения кривой депрессии и т.п.).
1.7. Результаты прогнозирования трансформации русел рек в нижних бьефах необходимо учитывать при оценке влияния строительства и эксплуатации гидроузлов на природную среду, связанные с ней отрасли хозяйства (рыбное, лесное, сельское) и жизнедеятельности населения.
Совершенствование методов прогноза трансформации русла нижних бьефов гидроузлов должно базироваться на результатах мониторинга в процессе их эксплуатации и пополнения имеющихся баз данных.
Нормативные ссылки
1.8. В Рекомендациях приведены ссылки на следующие нормативные документы:
СНиП 33-01-2003. Гидротехнические сооружения. Основные положения / Госстрой России. М.: ФГУП ЦПП. 2004.
СНиП 2.02.01.83*. Основания зданий и сооружений / Госстрой России. М.: ФГУП ЦПП. 2003.
СП 33-101-2003. Определение основных расчетных гидрологических характеристик / Госстрой России. М.: ФГУП ЦПП. 2004.
ГОСТ 12536-79. Грунты. Методы лабораторного определения гранулометрического (зернового) и микроагрегатного состава. М.: Изд-во стандартов. 1988.
ГОСТ 20522-96. Грунты. Методы статистической обработки результатов испытания. М.: Изд-во стандартов. 1997.
РД-153-34.2-02.409-2003. Методические указания по оценке влияния гидротехнических сооружений на окружающую среду / ВНИИГ. СПб. 2003.
Рекомендации по анализу данных и контролю состояния водосбросных сооружений и нижних бьефов гидроузлов: П 75-2000 / ВНИИГ. СПб. 2000.
Терминология и условные обозначения
1.9. Термины, используемые в Рекомендациях, даны в трактовке СО 34.21.308-2005. Гидротехника. Основные понятия. Термины и определения. РАО «ЕЭС России». СПб: Изд-во ВНИИГ им. Б.Е. Веденеева. 2005.
1.10. В работе приняты следующие основные обозначения и определения (обозначения, имеющие вспомогательный характер и использованные не более 2 - 3 раз, в перечень не включены):
Q - расход воды, м3/с;
у = Н - уровень свободной поверхности воды, м;
z - отметка дна, м;
Q = f(H) - зависимость расходов от уровней воды в рассматриваемом створе;
h - средняя по живому сечению глубина потока, в условиях плановой задачи - глубина потока в точке с заданными плановыми координатами, м;
hбр - средняя глубина русла от дна до уровня бровок, м;
hкон - средняя глубина, устанавливающаяся в русле, сложенном разно-зернистым грунтом, после его размыва и образования слоя самоотмостки, м;
В - ширина русла по урезу воды, м;
Вф - ширина фиктивного прямоугольного русла, схематизирующего естественное русло реки, м;
V - средняя (по живому сечению) скорость потока, м/с;
Vн - неразмывающая скорость, то есть такая средняя скорость потока, при которой в условиях равномерного режима течения и весьма малых уклонов дна наблюдается лишь шевеление отдельных частиц грунта данной крупности d без их срыва, м/с;
Vнi - неразмывающая скорость потока при уклоне дна, существенно отличном от нуля, м/с;
Vн.отм - неразмывающая скорость потока для материала естественной отмостки дна в русле, сложенном разнозернистым материалом, м/с;
uд.н - придонная (на высоте выступов шероховатости) неразмывающая скорость потока, м/с;
u* - динамическая скорость, м/с;
ω - площадь живого сечения, м2;
Qмакс - максимальный расход паводка, м3/с;
Qрф - руслоформирующий расход воды, то есть расход воды, соответствующий среднемноголетнему расходу наносов, м3/с;
Qs - расход наносов, то есть количество наносов, транспортируемых потоком через рассматриваемое живое сечение в единицу времени, м3/с;
Ps - транспортирующая способность потока, то есть предельное количество наносов с заданными физико-механическими характеристиками, которое поток с заданными гидромеханическими характеристиками может транспортировать в единицу времени, м3/с;
Рр - размывающая способность потока, то есть количество грунта с заданными физико-механическими характеристиками, которое поток с заданными гидромеханическими характеристиками может размыть на единице площади русла в единицу времени, м/с;
qs - приходящийся на единицу длины потока расход притока (или оттока) наносов, происходящего в процессе массообмена потока и русла при русловых переформированиях, м2/с;
S - средняя концентрация руслоформирующих фракций наносов в потоке, то есть среднее по живому сечению объемное содержание наносов в единице объема пространства, занятого русловым потоком;
δ - пористость донных отложений, то есть отношение объема пор к общему объему грунта;
ΔΩ - объем деформации русла в пределах расчетного участка за интервал времени Δt, м3;
t - время, с;
Δt - расчетный интервал времени, с;
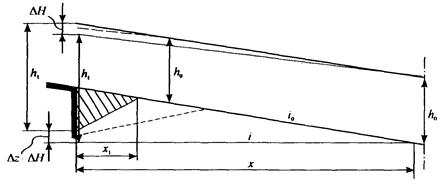
х - длина русла, исчисляемая от начального створа, м;
Δх - длина расчетного участка, м;
k = (1, 2, ..., K) - номер расчетного участка и его низового створа;
k = 0 - номер начального створа расчета (при расчете деформаций в нижнем бьефе - створа гидроузла);
k = K - номер низового створа исследуемого бьефа, ниже которого русловые переформирования не распространяются;
С - коэффициент Шези, [м1/2/с];
nш - коэффициент шероховатости русла в формулах показательного вида для определения коэффициента Шези [мm-1/2·с];
m - показатель степени в формулах показательного вида для С;
i - уклон дна схематизированного русла;
i0 - первоначальный уклон дна при приближенной оценке общего размыва;
if - уклон трения;
æ - гидравлический показатель русла;
d - диаметр частиц грунта; средний диаметр однозернистого грунта или средний диаметр частиц фракции; приведенный диаметр, то есть диаметр шара, объем которого равен среднестатистическому объему частиц данной фракции, мм, м;
d95, d50 и d5 - диаметры частиц, мельче которых в грунте содержится соответственно 95, 50 и 5 % (по кривой гранулометрического состава), мм, м;
dотм - средняя крупность материала отмостки разнозернистого грунта, мм, м;
ρw - плотность воды, кг/м3, т/м3;
ρs - плотность материала наносов, кг/м3, т/м3;
ρгр - плотность грунта в донных отложениях, кг/м3, т/м3;
w - гидравлическая крупность частиц наносов, м/с;
![]() - коэффициент сопротивления частиц наносов
при равномерном обтекании их потоком со скоростью равной w;
- коэффициент сопротивления частиц наносов
при равномерном обтекании их потоком со скоростью равной w;
![]() - число Рейнольдса для того же случая
обтекания;
- число Рейнольдса для того же случая
обтекания;
![]() - параметр формы зерен несвязного грунта, где
d - приведенный диаметр, а и b - средневзвешенные длина и ширина максимального
сечения частицы грунта;
- параметр формы зерен несвязного грунта, где
d - приведенный диаметр, а и b - средневзвешенные длина и ширина максимального
сечения частицы грунта;
c - среднее значение сцепления связного грунта, кПа;
срасч - расчетное значение сцепления связного грунта, кПа;
α - корректив количества движения (корректив Кориолиса), обычно принимаемый равным 1,0 - 1,1;
v - кинематический коэффициент вязкости воды, см2/с; м2/с;
t° - температура воды (градус Цельсия).
Примечание: В п. 1.10 указаны наиболее употребляемые в практике единицы измерения величин, которые при проведении расчетов по формулам, удовлетворяющим принципу размерности, должны быть приведены в единой системе (например, все линейные величины - в м, масса - в кг, время - в с и т.д.). В квадратных скобках указаны единицы измерения величин, входящих в эмпирические формулы, не удовлетворяющие принципу размерности; соблюдение этих единиц измерения при расчетах обязательно. Величины, единицы измерения которых не указаны, являются безразмерными.
2. ОСОБЕННОСТИ ПРОЯВЛЕНИЯ РУСЛОВОГО ПРОЦЕССА В НИЖНИХ БЬЕФАХ
2.1. На разных стадиях строительства, в период его завершения и на разных этапах эксплуатации гидроузла его влияние на русло в нижнем бьефе имеет свои особенности, определяющие ход руслового процесса и приводящие к тем необратимым изменениям в речном русле, которые могут в большей или меньшей мере оказывать влияние как на сам гидроузел, так и на элементы природно-технического комплекса его нижнего бьефа (см. РД-153-34.2-02.409-2003 и [7]).
Период строительства гидроузла
2.2. На участке русла, стесненном перемычками, а затем и строящимися сооружениями, происходят интенсивные местные деформации.
2.3. Объем размыва в русле реки и в отводящих каналах водопропускных сооружений гидроузла (включая размыв перемычек) может значительно превосходить объем твердого стока, соответствующий транспортирующим возможностям потока в естественном русле.
В этом случае ниже строящихся сооружений поток откладывает часть наносов в виде бара или переката, отметки гребня которого постепенно могут нарастать по мере развития местного размыва.
Особенно интенсивно этот процесс протекает на завершающих этапах строительства, когда в силу различных обстоятельств пропуск расходов реки через строящееся сооружение осуществляется со значительной неравномерностью его распределения по ширине реки, характеризующейся во многих случаях сосредоточением большей части пропускаемого в нижний бьеф расхода воды на весьма узком участке ширины отводящего русла.
Начальный период эксплуатации гидроузла
2.4. Вследствие развития за водопропускными сооружениями ямы местного размыва может происходить дальнейшее образование расположенного ниже нее бара или переката. По мере затухания процесса местного размыва за сооружениями рост бара (переката) замедляется, происходит его частичный или полный размыв и смещение вниз по течению.
2.5. В ряде случаев перекат, образовавшийся из продуктов местного размыва, создает временный подъем уровней и подпор на сооружения гидроузла со стороны нижнего бьефа. Со временем подпор уменьшается, что обычно связано с постепенным смывом переката, продвижением вниз по течению зоны отложений и общим понижением уровней нижнего бьефа.
2.6. Пропуск паводков малой обеспеченности может вызвать очень быстрое продвижение переката (п. 2.4) вниз по течению. В этом случае подпор, создаваемый этим перекатом, может не распространяться до створа гидроузла, где может отмечаться понижение уровней за счет преобладания общего размыва русла на участке, расположенном между гидроузлом и перекатом (п. 2.7).
Последующая эксплуатация гидроузла
2.7. Поступающий в нижний бьеф из водохранилища осветленный поток после завершения или временной стабилизации процесса местного размыва за сооружениями начинает постепенно размывать русло нижнего бьефа, перемещая зону отложений наносов вниз по течению. Преобладающим видом необратимой деформации русла выше по течению является размыв.
2.8. Зона размыва, распространяясь вслед за зоной отложений, постепенно охватывает все большую длину бьефа, оставляя выше по течению участок более устойчивого, чем в бытовом состоянии, русла. При взаимодействии этого русла с потоком не происходит уже значительных деформаций дна реки и существенного насыщения потока наносами. Повышение устойчивости русла в зоне общего размыва обусловлено увеличением глубин, снижением скоростей потока и, как следствие, уменьшением подвижности донного материала по сравнению с бытовыми условиями.
2.9. Характер распространения зоны размыва зависит от уклона реки, геологического строения ее ложа и т.д. [25]. При малом уклоне, не очень больших скоростях течения, больших скоплениях аллювия (в том числе, в виде островов, побочней и т.п.) общий размыв развивается в длину сравнительно медленно. Несмотря на это большие глубины размыва могут привести к понижению уровней воды, особенно ощутимому при сравнительно малых расходах воды.
2.10. При ограничении размывов коренными породами или образованием естественной отмостки, чему особенно благоприятствует сложное геологическое строение русла, общий размыв может быстро развиваться в длину, особенно при больших уклонах. Снижение уровней воды в этих случаях происходит быстрее, чем в случае, описанном в п. 2.9. Быстрее происходит и стабилизация этого процесса [25].
2.11. В зоне общего размыва происходит уменьшение извилистости русла и выравнивание разницы между объемами русла на плесовых и перекатных участках. На судоходных реках в ряде случаев этому процессу способствуют дноуглубительные работы на перекатах и устройство капитальных прорезей. В результате при значительной зарегулированности водотока с течением времени может произойти исчезновение специфических особенностей речного русла, его мезо- и макроформ [2, 24], и оно приобретет форму, приближающуюся к форме канала.
2.12. Процесс трансформации русла нижнего бьефа, имеющий общую тенденцию к затуханию русловых переформирований и стабилизации русла на участке большой протяженности, заметно интенсифицируется при прохождении паводков более высоких, чем паводки предшествующих лет.
2.13. В зоне влияния суточного регулирования мощности гидроэлектростанции при прохождении волн попусков происходит повышение размывающей и транспортирующей способностей потока. По мере удаления от ГЭС волны попуска затухают и их роль в интенсификации размыва русла и транспорта наносов ослабевает. Следствием этого является усиление размывов на примыкающем к гидроузлу участке русла и отложение наносов ниже по реке [25].
2.14. Резкие колебания уровней нижнего бьефа, обусловленные суточным регулированием мощности ГЭС, могут явиться причиной суффозии грунта береговых откосов фильтрационным потоком, направленным в русло, при резком спаде уровней и, как следствие этого, возникновения и развития боковой эрозии - обрушения и оползания берегов. Приток наносов, происходящий за счет боковой эрозии, увеличивает заносимость перекатов и уменьшает их устойчивость, несколько затормаживая процесс распространения зоны размыва.
2.15. При неустановившемся течении воды, вызванном прохождением волн попусков суточного регулирования, может происходить интенсификация грядового движения наносов [32, 40], приводящая к уменьшению устойчивости перекатов и повышению заносимости судоходных прорезей в зоне отложений.
2.16. При существенной срезке паводков и уменьшении затопления отмелей может произойти закрепление и зарастание побочней и преобразование их в элементы поймы. В конечном итоге это явление может привести к увеличению извилистости русла вопреки общей тенденции к его спрямлению при зарегулировании стока (п. 2.11).
2.17. В местах слияния зарегулированных рек с их незарегулированными притоками отмечается увеличение отложений на перекатах [30, 32, 49]. Причиной роста отложений является задержка и снижение пика паводка основной реки и обусловленное этим увеличение уклонов свободной поверхности в устьевой части притока, приводящее к возрастанию скоростей притока и выносу наносов, осаждающихся в русле основной реки.
Нередко в зоне впадения притоков образуются перекаты типа россыпей, при смещении которых вниз по течению происходит их слияние и образование осередков. Впоследствии эти осередки могут превратиться в острова, разделяющие поток на рукава и протоки.
2.18. На трансформацию русла нижнего бьефа существенное влияние могут оказывать карьерные разработки - извлечение песка и гравийно-галечникового грунта из русла, производимое с целью получения материалов для нужд строительного производства. Изъятие грунта приводит не только к местному понижению дна водотока, но также интенсифицирует размыв дна выше и ниже карьера. При проведении карьерных разработок в руслах, сложенных разнозернистым грунтом, нарушается процесс образования естественной отмостки, что также способствует усилению размыва дна.
2.19. В нижних бьефах гидроузлов, находящихся в подпоре нижележащего водоема (водохранилища, озера, моря), развитие процесса трансформации русла остается в основном таким же, как и в нижних бьефах неподпертых гидроузлов, проявляясь главным образом на примыкающем к ГЭС участке реки.
2.20. При увеличении поступления в нижний бьеф наносов из водохранилища по мере его заиления, а также при промыве водохранилища или отстойников может происходить интенсивная заносимость (завал) русла реки в нижних бьефах, обусловленная значительным превышением поступающего в нижний бьеф расхода наносов над транспортирующей способностью потока в русле с уклоном, пониженным по сравнению с бытовым в результате общего размыва.
3. ОСНОВНЫЕ РАСЧЕТНЫЕ ХАРАКТЕРИСТИКИ НАНОСОВ И ГРУНТОВ, СЛАГАЮЩИХ РУСЛО
Механические характеристики
3.1. Грунты, образующие русло, делятся на связные и несвязные (сыпучие). Связные грунты характеризуются наличием сцепления между отдельными частицами; примером таких грунтов являются глины, суглинки, супеси.
В несвязных (сыпучих) грунтах сцепление между частицами практически отсутствует. К несвязным грунтам относятся илы, пески (в том числе пылеватые), гравий, галька, булыжник.
Деление на связные и несвязные грунты является условным, так как между частицами несвязного грунта крупностью менее 0,25 мм (см. п. 3.15) возникают силы сцепления, которые необходимо учитывать при определении порога троганья. В свежих отложениях мелкозернистые грунты, содержащие глинистые частицы, ведут себя преимущественно как несвязные, а по мере уплотнения начинают проявлять свойства связных грунтов.
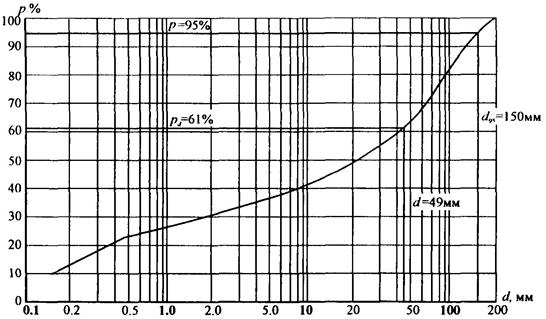
3.2. Крупность речных наносов определяется их механическим анализом (ГОСТ 12536-79), на основании которого строится кривая гранулометрического состава (рис. 1).
Рис. 1. Кривая гранулометрического состава наносов
3.3. Грунт предполагается однородным по крупности при коэффициенте разнозернистости d95/d5 ≤ 5. При расчетах отмостки, образующейся в процессе размыва разнозернистого грунта, однородным считается грунт, характеризуемый значением Ko = d/d95 > 0,6.
3.4. Плотность материала речных наносов ρs изменяется в зависимости от их минералогического состава [10] (табл. 1). При отсутствии данных специальных изысканий средняя плотность речных наносов может быть принята равной 2,65 т/м3.
Таблица 1
Плотность материала речных наносов различного минералогического состава
|
Плотность ρs, т/м3 |
Породы |
Плотность ρs, т/м3 |
|
|
Известняк |
2,46 - 2,84 |
Трахиты и кремень |
2,60 - 2,80 |
|
Песчаник |
2,20 - 2,50 |
Граниты |
2,51 - 3,05 |
|
Гнейс |
2,40 - 2,70 |
Базальты |
2,70 - 3,20 |
|
Кварц, шпат и мрамор |
2,50 - 2,83 |
Корунд и тяжелый шпат |
3,30 - 4,50 |
3.5. Плотность грунта ρгр в аллювиальных отложениях определяется пористостью отложений δ и плотностью материала наносов ρs
ρгр = (1 - δ)ρs. (1)
При отсутствии данных изысканий значение может быть принято по табл. 2.
3.6. Пористость грунта, определяемая как отношение объема пор к общему объему грунта, различна для однородных наносов разной крупности и изменяется в пределах, указанных в табл. 3 [10, 19].
В механике грунтов часто употребляется понятие коэффициент пористости е, определяемое как отношение объема пор к объему твердой части грунта. Связь между пористостью и коэффициентом пористости представляется соотношением δ = е/(1 + е). Использование в расчетах русловых процессов и транспорта наносов понятие пористости является более удобным, поскольку оно непосредственно связано с концентрацией наносов на дне водотока: s + δ = 1.
Таблица 2
Плотность донных отложении ρгр в зависимости от их состава
|
Наименование фракций, диаметр частиц, мм, и пределы их содержания в % по весу |
ρгр, кг/м3 |
||||||||||||||
|
глина |
ил |
пыль |
песок |
гравий |
галька |
||||||||||
|
<0,001 |
0,001 - 0,005 |
0,005 - 0,01 |
0,01 - 0,05 |
0,05 - 0,1 |
0,1 - 0,2 |
0,2 - 0,5 |
0,5 - 1,0 |
1 - 2 |
2 - 5 |
5 - 10 |
10 - 20 |
20 - 50 |
50 - 100 |
||
|
Илы гонкие |
10 - 20 |
60 - 70 |
10 - 20 |
700 - 800 |
|||||||||||
|
Илы |
60 - 80 |
20 - 40 |
800 - 900 |
||||||||||||
|
Илы с примесью песка |
10 - 20 |
60 - 70 |
10 - 20 |
900 - 1100 |
|||||||||||
|
Пылеватые и мелкие пески заиленные |
10 - 20 |
40 - 70 |
20 - 40 |
1100 - 1200 |
|||||||||||
|
Пылеватые мелкие и средние пески заиленные |
10 - 20 |
40 - 70 |
20 - 40 |
1200 - 1300 |
|||||||||||
|
Средние пески заиленные |
10 - 20 |
20 - 40 |
40 - 70 |
1300 - 1500 |
|||||||||||
|
Мелкие пески |
20 - 40 |
40 - 70 |
10 - 20 |
1500 - 1600 |
|||||||||||
|
Средние пески |
10 - 20 |
20 - 40 |
40 - 70 |
1600 - 1700 |
|||||||||||
|
Средние и крупные пески |
20 - 40 |
60 - 70 |
1600 - 1800 |
||||||||||||
|
Пески с гравием |
60 - 70 |
20 - 40 |
1700 - 2100 |
||||||||||||
|
Гравий |
10 - 20 |
60 - 70 |
10 - 20 |
1800 - 2100 |
|||||||||||
|
Галька с гравием |
20 - 40 |
60 - 70 |
2000 - 2400 |
||||||||||||
Примечания: 1. Приведенные здесь значения ρгр соответствуют плотному залеганию грунтов; для свежих отложений значения ρгр должны быть уменьшены.
2. В таблице не учитывается содержание органических веществ, уменьшающих значение ρгр на 20 - 30 и 30 - 50 % при содержании органических остатков соответственно 5 и 10 %.
3. За основу таблицы приняты несколько скорректированные данные [19, табл. 13.2].
Таблица 3
Показатели пористости грунтов различной крупности
|
Размеры частиц грунта, мм |
Пористость δ |
Коэффициент пористости е |
||
|
от - до |
средний |
|||
|
Глина |
< 0,001 |
0,52 - 0,29 |
0,34 - 0,22 |
|
|
Ил |
||||
|
мелкий |
0,001 - 0,005 |
0,003 |
0,80 - 0,70 |
0,44 - 0,41 |
|
крупный |
0,005 - 0,01 |
0,0075 |
0,80 - 0,65 |
0,44 - 0,39 |
|
Пыль |
||||
|
мелкая |
0,01 - 0,05 |
0,03 |
0,65 - 0,50 |
0,39 - 0,33 |
|
крупная |
0,05 - 0,1 |
0,075 |
0,50 - 0,35 |
0,33 - 0,26 |
|
Песок |
||||
|
мелкий |
0,1 - 0,2 |
0,15 |
0,45 - 0,35 |
0,31 - 0,26 |
|
средний |
0,2 - 0,5 |
0,35 |
0,45 - 0,35 |
0,31 - 0,26 |
|
крупный |
0,5 - 1 |
0,75 |
0,40 - 0,28 |
0,29 - 0,22 |
|
Гравий |
||||
|
мелкий |
1 - 2 |
1,5 |
0,40 - 0,28 |
0,29 - 0,22 |
|
средний |
2 - 5 |
3,5 |
0,40 - 0,28 |
0,29 - 0,22 |
|
крупный |
5 - 10 |
7,5 |
0,40 - 0,28 |
0,29 - 0,22 |
|
Галька |
||||
|
мелкая |
10 - 20 |
15 |
0,40 - 0,28 |
0,29 - 0,22 |
|
средняя |
20 - 50 |
35 |
0,40 - 0,28 |
0,29 - 0,22 |
|
крупная |
50 - 100 |
75 |
0,40 - 0,28 |
0,29 - 0,22 |
|
Валуны |
||||
|
средние |
100 - 200 |
150 |
0,40 - 0,28 |
0,29 - 0,22 |
|
мелкие |
200 - 500 |
350 |
0,40 - 0,28 |
0,29 - 0,22 |
|
крупные |
500 - 1000 |
750 |
0,40 - 0,28 |
0,29 - 0,22 |
Примечание. Большие значения δ и е относятся к грунтам, частицы которых имеют окатанную форму, меньшие - к грунтам, сложенным частицами пластинчатой формы (см. п. 3.9).
3.7. Крупность однородного грунта, а также крупность отдельных фракций разнозернистого грунта определяется среднеарифметическим размером отверстий сит, ограничивающих рассматриваемую фракцию.
В некоторых случаях (при определении гидравлической крупности, высоты зернистой шероховатости и т.п.) для повышения точности расчета целесообразно использовать в качестве геометрической характеристики крупности наносов приведенный диаметр, то есть диаметр шара, объем которого равен среднестатистическому объему частиц данной фракции.
Для определения приведенного диаметра по данным ситового анализа могут быть использованы следующие формулы [5], справедливые для частиц грунта наиболее распространенной формы θ = 0,73 (см. п. 3.9):
при использовании штампованных сит с круглыми отверстиями
d = 0,90d○, (2)
при использовании плетеных сит с квадратными отверстиями
d = 11,7d□, (3)
где d○ и d□ - соответственно среднеарифметические размеры отверстий (круглой или квадратной формы), ограничивающих рассматриваемую фракцию.
Примечание. В стандартном наборе сит с отверстиями 0,14; 0,315; 0,63; 1,25; 2,5; 5; 10; 20 и 40 мм плетеными (с квадратными отверстиями) являются сита размером 0,14 - 2,5 мм, остальные сита имеют круглые отверстия. В стандартном наборе сит с отверстиями 0,1; 0,25; 0,5; 1; 2; 3; 5; 7 и 10 мм плетеными являются сита размером 0,1 - 0,5 мм, остальные сита имеют круглые отверстия.
3.8. Крупность мельчайших частиц (< 0,1 мм) определяется на основании исследования их гидравлической крупности путем осаждения частиц в воде. Определение размера частиц по их гидравлической крупности производится по данным, приводимым в п. 3.11.
3.9. Форма зерен несвязного грунта может быть охарактеризована параметром [43]
![]() (4)
(4)
где а и b - длина и ширина максимального сечения частицы; d - приведенный диаметр частицы.
Как правило, для естественных речных наносов параметр формы изменяется от θ = 0,5 для пластинчатых частиц до θ = 1 для шарообразных частиц. При отсутствии данных непосредственных измерений значение θ может быть принято равным 0,73, что соответствует некоторой осредненной (наиболее часто встречающейся) форме частиц.
3.10. Одной из основных характеристик сопротивляемости грунта размыву является его удельное сцепление, определяемое на основании испытаний образцов грунта на срез.
Нормативные значения сн вычисляются по методу наименьших квадратов для всей совокупности исследованных образцов в соответствии с ГОСТ 20522-96. При вычислении предельных неразмывающих скоростей необходимо учитывать коэффициент безопасности Kс, характеризующий вероятность отклонения сил сцепления от нормативного значения,
где σ - среднее квадратическое отклонение значений c от cн; tα - коэффициент, принимаемый по табл. Ж.2 ГОСТ 20522-96 в зависимости от числа испытаний и заданной односторонней доверительной вероятности α, которую в расчетах русловых процессов следует приравнивать 0,95.
При отсутствии данных испытаний образцов грунта на срез Kc может быть приближенно принято равным 2.
Для предварительных расчетов cн связных грунтов может определяться по табл. 4 в зависимости от основных характеристик грунта, консистенции JL и пористости δ.
Таблица 4
Средние значения нормативного сцепления сн связных грунтов, кПа = т/м ∙ с2
|
Консистенция JL |
Пористость δ |
||||||||||
|
0,300 |
0325 |
0350 |
0375 |
0,400 |
0,425 |
0,40 |
0,475 |
0,500 |
0,525 |
||
|
Супеси |
0 - 0,25 |
16,5 |
13,5 |
11,5 |
9 |
7,5 |
- |
- |
- |
- |
- |
|
0,25 - 0,75 |
14 |
11,5 |
9,5 |
7 |
5 |
3,5 |
- |
- |
- |
- |
|
|
0 - 0,25 |
49,5 |
44 |
38 |
33,5 |
29,5 |
25,5 |
22,5 |
20,0 |
18 |
- |
|
|
Суглинки |
0,25 - 0,50 |
40 |
37,5 |
35 |
31 |
27 |
23 |
19 |
16,5 |
15,5 |
- |
|
0,50 - 0,75 |
- |
- |
- |
27,5 |
24 |
20,5 |
17 |
15 |
13 |
11 |
|
|
0 - 0,25 |
- |
- |
81,5 |
74,5 |
65 |
55 |
49 |
43,5 |
38,5 |
33,5 |
|
|
Глины |
0,25 - 0,50 |
- |
- |
- |
60,5 |
56 |
51 |
45 |
39,5 |
34,5 |
29,5 |
|
0,50 - 0,75 |
- |
- |
- |
47 |
44,5 |
41 |
38 |
34,5 |
31 |
26,5 |
|
Примечание. Таблица составлена на основе данных СНиП 2.02.01-83*, табл. 2 прил. 1.
Консистенция грунта находится по формуле
![]() (6)
(6)
где Wн - природная влажность грунта в долях единицы; WL и Wр - соответственно влажность на границе текучести и на границе скатывания (пластичности).
Гидравлическая крупность наносов
3.11. Гидравлическая крупность w частиц несвязного грунта может быть определена в зависимости от их приведенного диаметра d и плотности ρs, а также от кинематического коэффициента вязкости при известной температуре t° (рис. 2) и плотности воды ρw по формуле А.Б. Векслера [6]
где

Режимы обтекания частиц потоком обычно определяют по числу Рейнольдса в несколько иной форме записи:
![]()
Рис. 2. Зависимость кинематического коэффициента вязкости воды v от температуры t °С
Для мельчайших частиц (d < 0,10 мм), характеризующихся ламинарным режимом
обтекания при свободном падении ![]() , зависимость (7) может использоваться в упрощенном виде
, зависимость (7) может использоваться в упрощенном виде
при d < 0,05 мм (Re < 0,1) эта формула преобразуется в более простую зависимость Стокса

Для частиц крупностью d ≥ 2,5 мм, характеризующихся турбулентным режимом обтекания (Re ≥ 400), зависимость (7) приобретает вид
Шкала гидравлической крупности частиц грунта w в зависимости от их приведенного диаметра d в соответствии с формулами (7) - (9) для наносов, имеющих плотность частиц ρs = 2650 кг/м3, приведена на рис. 3 и в табл. 5. При пользовании этими данными влияние отличия плотности ρs от 2650 кг/м3 на гидравлическую крупность может быть учтено поправочным коэффициентом βр по формуле
w = βpwг, (10)
где wг - значение гидравлической крупности частиц при ρs = 2650 кг/м3 по данным графика рис. 3 или табл. 5;
где Re приближенно может приниматься равным ![]() Зависимость (11)
для частиц, соответствующих ламинарному (Re ≤ l) и турбулентному (Re ≥ 400) режимам обтекания, существенно упрощается за счет
того, что показатель степени k принимает практически постоянные значения: k = 1 при Re < 1 и k = 0,5 при Re ≥ 400.
Зависимость (11)
для частиц, соответствующих ламинарному (Re ≤ l) и турбулентному (Re ≥ 400) режимам обтекания, существенно упрощается за счет
того, что показатель степени k принимает практически постоянные значения: k = 1 при Re < 1 и k = 0,5 при Re ≥ 400.
3.12. Форма частиц при определении гидравлической крупности может быть учтена поправочным коэффициентом βw по формуле
wθ = βww, (12)
где βw определяется зависимостью А.Б. Векслера [6], основанной на экспериментальных данных В.В. Романовского [41],
Влияние формы не сказывается на гидравлической крупности частиц, характеризующихся ламинарным режимом обтекания при свободном падении, то есть при Re < 1 коэффициент βw = 1. Наиболее ощутимо влияние формы для частиц с турбулентным режимом обтекания (Re ≥ 400), для которых формула (13) несколько упрощается
βw = 2,4θ - 0,75. (14)
При θ = 0,73 поправочный коэффициент βw = 1. Число Re, входящее в зависимость (13), может приниматься соответствующим значению w по графику на рис. 3 или табл. 5 с учетом поправки βр.
3.13. При значительном содержании наносов
(концентрация S ![]() 1 % или
мутность ε
1 % или
мутность ε ![]() 25 кг/м3) вместо гидравлической крупности,
характеризующей поведение в потоке одиночных частиц, следует использовать
групповую гидравлическую крупность, учитывающую взаимное влияние частиц наносов
на поведение отдельной частицы и определяемую в соответствии с рекомендациями,
содержащимися в [5, 14].
25 кг/м3) вместо гидравлической крупности,
характеризующей поведение в потоке одиночных частиц, следует использовать
групповую гидравлическую крупность, учитывающую взаимное влияние частиц наносов
на поведение отдельной частицы и определяемую в соответствии с рекомендациями,
содержащимися в [5, 14].
Неразмывающие скорости
3.14. Неразмывающая скорость для данного грунта характеризует устойчивость его на дне потока. При этом могут быть выделены различные состояния, соответствующие разной степени надежности или разной вероятности срыва частиц со дна потока. В частности, принято различать два состояния, первое из которых определяет устойчивость отдельных зерен грунта на дне потока, второе - устойчивость поверхностного слоя грунта в целом.
Рис. 3. Зависимость гидравлической крупности частиц наносов w от их приведенного диаметра d и температуры воды t °С (при коэффициенте формы θ = 0,73)
Таблица 5
Гидравлическая крупность частиц наносов плотностью ρs = 2,65 т/м3 и с коэффициентом формы θ = 0,73
А. Ламинарный и переходный режимы осаждения
|
Приведенный диаметр d, мм |
Гидравлическая крупность w, м/с, при температуре t °С |
||||||
|
0° |
5° |
10° |
15° |
20° |
25° |
30° |
|
|
0,0050 |
0,0000125 |
0,0000148 |
0,0000172 |
0,0000197 |
0,0000228 |
0,0000251 |
0,0000280 |
|
0,0075 |
0,0000282 |
0,0000333 |
0,0000387 |
0,0000443 |
0,0000502 |
0,0000564 |
0,0000629 |
|
0,010 |
0,0000502 |
0,0000592 |
0,0000688 |
0,0000778 |
0,0000893 |
0,000100 |
0,000112 |
|
0,015 |
0,0001129 |
0,0001332 |
0,0001547 |
0,000177 |
0,000201 |
0,000226 |
0,000252 |
|
0,020 |
0,000201 |
0,000237 |
0,000275 |
0,000315 |
0,000357 |
0,000400 |
0,000446 |
|
0,025 |
0,000314 |
0,000370 |
0,000429 |
0,000492 |
0,000557 |
0,000624 |
0,000696 |
|
0,030 |
0,000451 |
0,000532 |
0,000617 |
0,000707 |
0,000800 |
0,000897 |
0,000999 |
|
0,040 |
0,000800 |
0,000942 |
0,00109 |
0,00125 |
0,00141 |
0,00158 |
0,00176 |
|
0,050 |
0,00125 |
0,00147 |
0,00168 |
0,00194 |
0,00219 |
0,00244 |
0,00271 |
|
0,075 |
0,00276 |
0,00323 |
0,00371 |
0,00420 |
0,00469 |
0,00519 |
0,00569 |
|
0,100 |
0,00476 |
0,00552 |
0,00625 |
0,00702 |
0,00774 |
0,00844 |
0,00912 |
|
0,125 |
0,00713 |
0,00816 |
0,00914 |
0,01009 |
0,0110 |
0,01198 |
0,01275 |
|
0,150 |
0,00971 |
0,01095 |
0,01217 |
0,0133 |
0,0143 |
0,0154 |
0,0165 |
|
0,175 |
0,01241 |
0,0138 |
0,0152 |
0,0166 |
0,0178 |
0,0191 |
0,0202 |
|
0,20 |
0,01518 |
0,0168 |
0,0184 |
0,0199 |
0,0213 |
0,0227 |
0,0241 |
|
0,25 |
0,0208 |
0,0228 |
0,0248 |
0,0267 |
0,0285 |
0,0302 |
0,0320 |
|
0,30 |
0,0266 |
0,0292 |
00315 |
0,0337 |
0,0360 |
0,0381 |
0,0400 |
|
0,35 |
0,0324 |
0,0354 |
0,0381 |
0,0408 |
0,0433 |
0,0456 |
0,0479 |
|
0,40 |
0,0385 |
0,0419 |
0,0452 |
0,0480 |
0,0507 |
0,0582 |
0,0555 |
|
0,45 |
0,0444 |
0,0483 |
0,0519 |
0,0549 |
0,0577 |
0,0603 |
0,0627 |
|
0,5 |
0,0508 |
0,0547 |
0,0584 |
0,0617 |
0,0546 |
0,0671 |
0,0694 |
|
0,6 |
0,0628 |
0,0671 |
0,0708 |
0,0743 |
0,0755 |
0,0804 |
0,0828 |
|
0,7 |
0,0745 |
0,0786 |
0,0822 |
0,0857 |
0,0890 |
0,0921 |
0,0948 |
|
0,8 |
0,0854 |
0,0892 |
0,0940 |
0,0977 |
0,1007 |
0,1028 |
0,1044 |
|
0,9 |
0,0953 |
0,0999 |
0,1038 |
0,1073 |
0,1102 |
0,1126 |
0,1143 |
|
1,0 |
0,1045 |
0,1090 |
0,1129 |
0,1167 |
0,11% |
0,1218 |
0,1237 |
|
1,2 |
0,123 |
0,127 |
0,130 |
0,133 |
0,136 |
0,138 |
0,1402 |
|
1,4 |
0,139 |
0,143 |
0,146 |
0,149 |
0,151 |
0,153 |
0,154 |
|
1,6 |
0,154 |
0,158 |
0,160 |
0,163 |
0,165 |
0,166 |
0,167 |
|
1,8 |
0,167 |
0,170 |
0,173 |
0,176 |
0,178 |
0,179 |
0,180 |
|
2,0 |
0,180 |
0,183 |
0,185 |
0,187 |
0,189 |
0,190 |
0,190 |
|
2,2 |
0,191 |
0,194 |
0,197 |
0,199 |
0,199 |
0,199 |
0,199 |
|
2,5 |
0,210 |
0,211 |
0,212 |
0,212 |
0,212 |
0,212 |
0,212 |
Б. Турбулентный режим осаждения
|
Приведенный диаметр d, мм |
Гидравлическая крупность w, м/с |
Приведенный диаметр d, мм |
Гидравлическая крупность w, м/с |
Приведенный диаметр d, мм |
Гидравлическая крупность w, м/с |
|
3,0 |
0,232 |
7 |
0,355 |
40 |
0,848 |
|
3,5 |
0,251 |
8 |
0,379 |
50 |
0,948 |
|
4,0 |
0,268 |
9 |
0,402 |
75 |
1,161 |
|
4,5 |
0,284 |
10 |
0,424 |
100 |
1,341 |
|
5,0 |
0,300 |
12 |
0,465 |
150 |
1,642 |
|
5,5 |
0,315 |
15 |
0,519 |
200 |
1,897 |
|
6,0 |
0,328 |
20 |
0,600 |
250 |
2,120 |
|
6,5 |
0,342 |
30 |
0,735 |
300 |
2,323 |
При расчетах
трансформации русла предельную устойчивость грунта на дне потока, при которой происходит
лишь шевеление отдельных частиц грунта без их срыва, следует оценивать достижением погоном значения неразмывающей скорости Vн.
При превышении средней скоростью потока V значения Vн начинается срыв отдельных зерен, приводящий при скорости V = Vр к нарушению
устойчивости поверхностного слоя грунта. Скорость Vр, соответствующая этому состоянию взаимодействия руслового потока и
грунта на его дне, называется размывающей; численное значение ее может быть
определено согласно [11] по
формуле ![]()
При вычислении расхода наносов по формулам п. 4.10 в качестве определяющего параметра принята неразмывающая скорость Vн. Понятие размывающей (или допускаемой) скорости Vр обычно используется при оценке устойчивости крепления русла и содержит в себе некоторую степень риска [17, 37, 38].
Существующие методы определения Vн базируются на материале экспериментальных исследований поведения грунта под воздействием водного потока. Приводимые в пп. 3.15 - 3.16 формулы являются в настоящее время наиболее обоснованными.
Необходимо дальнейшее совершенствование способов определения Vн.
3.15. Для однородных по крупности несвязных грунтов (см. п. 3.3) значение Vн при движении воды, равномерном и близком к равномерному, и малых уклонах дна, в том числе при i = 0, может быть определено по формуле Ц.Е. Мирцхулавы [34, 38]
где uд.н - придонная (на высоте выступов шероховатости) неразмывающая скорость потока; mм - коэффициент, учитывающий влияние наносов, содержащихся в потоке в коллоидном состоянии; для чистых потоков mм = 1; при наличии в коллоидном состоянии наносов, мутность ε которых больше εо = 0,1 кг/м3, mм = 1,4; при промежуточных значениях ε коэффициент mм может быть принят по феноменологической зависимости
![]() (16)
(16)
 - коэффициент перегрузки, учитывающий изменение Vн под влиянием
пульсационного
характера скоростей вблизи дна и равный квадрату отношения максимальной
мгновенной скорости uд.макс к осредненной
скорости
- коэффициент перегрузки, учитывающий изменение Vн под влиянием
пульсационного
характера скоростей вблизи дна и равный квадрату отношения максимальной
мгновенной скорости uд.макс к осредненной
скорости ![]() на высоте выступов шероховатости; значение nм определяется по
приближенной формуле, имеющей по предложению А.Б. Векслера [6, 38]
следующий вид
на высоте выступов шероховатости; значение nм определяется по
приближенной формуле, имеющей по предложению А.Б. Векслера [6, 38]
следующий вид
![]() - усталостная прочность на разрыв
несвязного грунта, учитывающая появление сил сцепления между частицами мелкозернистого
грунта (d < 0,25
мм), которая для грунтов природного плотного сложения [6, 38]
определяется по зависимости
- усталостная прочность на разрыв
несвязного грунта, учитывающая появление сил сцепления между частицами мелкозернистого
грунта (d < 0,25
мм), которая для грунтов природного плотного сложения [6, 38]
определяется по зависимости
Kс - коэффициент безопасности (см. формулу (5)).
Для несвязных грунтов плотностью ρs = 2650 кг/м3 в потоках, свободных от наносов, значение Vн, можно принимать по графику рис. 4 или табл. 6. Отличие плотности материала наносов от ρs = 2650 кг/м3 может быть учтено с помощью коэффициента βр, на который умножаются значения Vн, приведенные в табл. 6 и на графике рис. 4.
![]() (19)
(19)
где ρs - плотность материала наносов, кг/м3.
Рис. 4. Зависимость неразмывающей скорости Vн несвязных грунтов от диаметра частиц d и глубины потока h (при плотности ρs = 2650 кг/м3, коэффициенте формы θ = 0,73, коэффициенте безопасности Kс = 2 и коэффициенте тн = 1)
Учет формы частиц песчаных и гравийно-галечниковых грунтов может быть приближенно осуществлен (по предложению А.Б. Векслера [6]) умножением значения Vн, полученного по формуле (15) или с помощью соответствующих ей табл. 6 и графика рис. 4, на поправочный коэффициент
полученный с использованием данных В.В. Романовского [42]. Влияние формы не сказывается на
значениях Vн частиц малых размеров, характеризующихся ламинарным
режимом обтекания при свободном падении: при ![]() βV = 1. Наиболее ощутимо
влияние формы для частиц с турбулентным режимом обтекания при свободном падении
(d > 2,5 мм, Re ≥ 400), для которых формула (20) несколько упрощается
βV = 1. Наиболее ощутимо
влияние формы для частиц с турбулентным режимом обтекания при свободном падении
(d > 2,5 мм, Re ≥ 400), для которых формула (20) несколько упрощается
βV = 2,2 - 1,65θ. (21)
Таблица 6
Неразмывающие скорости Vн для несвязных грунтов
|
Придонная скорость uд.н на высоте выступов шероховатости |
Средняя скорость Vн, м/с, при глубине потока h, м |
||||||||
|
наименование основного грунта |
разновидность (разнозернистый грунт, характеризуемый скоростью Vн, близкой к указанной) |
расчетный диаметр частицы d, мм |
0,5 |
1 |
3 |
5 |
10 |
||
|
Пыль |
Пыль и ил с мелким песком |
0,05 |
0,09 |
0,37 |
0,39 |
0,43 |
0,44 |
0,46 |
|
|
Песок |
мелкий |
Песок мелкий с примесью среднего |
0,10 |
0,08 |
0,27 |
0,29 |
0,32 |
0,33 |
0,35 |
|
0,15 |
0,07 |
0,25 |
0,27 |
0,30 |
0,31 |
0,32 |
|||
|
0,20 |
0,07 |
0,25 |
0,27 |
0,29 |
0,31 |
0,32 |
|||
|
средний |
Песок мелкий с глиной, песок средний с примесью крупного |
0,30 |
0,08 |
0,26 |
0,28 |
0,31 |
0,32 |
0,34 |
|
|
0,40 |
0,09 |
0,28 |
0,30 |
0,33 |
0,35 |
0,37 |
|||
|
крупный |
Песок среднезернистый с глиной с примесью гравия |
0,50 |
0,09 |
0,29 |
0,31 |
0,35 |
0,37 |
0,39 |
|
|
0,75 |
0,11 |
0,33 |
0,35 |
0,39 |
0,41 |
0,44 |
|||
|
Гравий |
мелкий |
Гравий мелкий с примесью крупного |
1,0 |
0,12 |
0,36 |
0,39 |
0,43 |
0,46 |
0,49 |
|
1,5 |
0,15 |
0,41 |
0,44 |
0,50 |
0,53 |
0,56 |
|||
|
средний |
Гравий средний с примесью песка крупного и мелкого гравия |
2,0 |
0,17 |
0,45 |
0,49 |
0,55 |
0,58 |
0,62 |
|
|
3,0 |
0,21 |
0,52 |
0,56 |
0,64 |
0,68 |
0,73 |
|||
|
4,0 |
0,24 |
0,57 |
0,63 |
0,72 |
0,76 |
0,81 |
|||
|
5,0 |
0,26 |
0,61 |
0,68 |
0,78 |
0,82 |
0,89 |
|||
|
крупный |
Гравий крупный с песком и мелким гравием |
5,0 |
0,26 |
0,61 |
0,68 |
0,78 |
0,82 |
0,89 |
|
|
7,50 |
0,33 |
0,70 |
0,78 |
0,90 |
0,96 |
1,04 |
|||
|
Галька |
мелкая |
Галька средняя с носком и гравием |
10,0 |
0,37 |
0,78 |
0,86 |
1,00 |
1,07 |
1,16 |
|
15,0 |
0,45 |
0,88 |
0,99 |
1,16 |
1,24 |
1,35 |
|||
|
средняя |
Галька крупная с примесью гравия |
20,0 |
0,52 |
0,97 |
1,09 |
1,29 |
1,38 |
1,51 |
|
|
30,0 |
0,63 |
1,10 |
1,25 |
149 |
1,60 |
1,75 |
|||
|
крупная |
Валуны мелкие с галькой и гравием |
40,0 |
0,73 |
1,19 |
1,37 |
1,65 |
1,78 |
1,95 |
|
|
50,0 |
0,83 |
1,27 |
1.46 |
1,78 |
1,92 |
2,12 |
|||
|
Валуны |
мелкие |
Валуны средние галькой |
75,0 |
1,01 |
- |
1,65 |
2,03 |
2,21 |
2,45 |
|
средние |
Валуны средние примесью крупных |
100,0 |
1,15 |
- |
1,79 |
2,23 |
2,44 |
2,71 |
|
|
150,0 |
1,41 |
- |
- |
2,54 |
2,79 |
3,13 |
|||
|
200,0 |
1,63 |
- |
- |
2,76 |
3,05 |
3,45 |
|||
|
300,0 |
1,99 |
- |
- |
3,10 |
3,46 |
3,94 |
|||
При θ = 0,73 поправочный коэффициент βV = 1. Число Рейнольдса, входящее в зависимости (20) и (21), может быть принято по значению w, определяемому по табл. 5, графику рис. 3 или зависимостям (7) - (8).
В предварительных расчетах и при отсутствии данных о крупности грунта значения Vн могут быть приближенно приняты согласно приводимому в табл. 6 описанию грунта, составленному с учетом данных [10].
3.16. Для несвязного грунта с крупностью частиц d > 2,5 мм, в котором силы сцепления пренебрежимо малы, а коэффициент перегрузки постоянен (nм = 4,3) и не зависит от d, неразмывающая скорость может быть определена по упрощенной формуле
3.17. В случае разнозернистости несвязного грунта, то
есть d95/d5 > 5 (см. п. 3.3), шероховатость русла определяется крупными
фракциями, в связи с чем в выражении под знаком логарифма в формулах (15) и (22) вместо d следует принимать d95. При
пользовании табл. 6 или графиком
рис. 4 полученные с их помощью
значения Vн должны быть умножены на поправочный коэффициент ![]()
3.18. Неразмывающая скорость для несвязных грунтов в неравномерных потоках может несколько отличаться от Vн в потоках равномерных и близких к равномерным при i = 0. В тех случаях, когда неравномерность спокойных потоков обусловлена прямыми или обратными уклонами дна -0,07 < i < 0,07 при близком к горизонтальному положению свободной поверхности потока, значение Vнi, учитывающее влияние уклона, может быть определено по приближенной полуэмпирической зависимости И.Г. Квасовой [20]
![]() (23)
(23)
где ζ - коэффициент,
учитывающий влияние уклона дна i и относительной
шероховатости d/h на распределение скорости по глубине потока; П - коэффициент, зависящий от
уклона дна и числа Фруда ![]() характеризующего условия предельного
равновесия грунта, в потоках, равномерных и близких к равномерному при i = 0. Численные значения ζ
и П определяются по графикам
рис. 5.
характеризующего условия предельного
равновесия грунта, в потоках, равномерных и близких к равномерному при i = 0. Численные значения ζ
и П определяются по графикам
рис. 5.
При положительных уклонах дна 0 < i < 0,07 значение Vнi может быть определено по упрощенной зависимости
![]() (24)
(24)
Рис. 5. Графики для определения коэффициентов ξ = f(d/h, i) и П = f(i, Fr)
3.19. Для связных грунтов неразмывающие скорости Vн следует определять [34, 38] по формуле Ц.Е. Мирцхулавы
где uд.н - придонная неразмывающая
скорость; d - приведенный диаметр агрегатов (отрывающихся отдельностей)
связного грунта, м; при отсутствии данных специальных исследований может быть
принято d = 4 мм; nм - для связных грунтов при отсутствии данных
модельных или натурных исследований следует принимать пм = 4; mм
- см. п. 3.15; Kc - см. п. 3.10; ![]() - усталостная прочность на разрыв
связного грунта, определяемая в зависимости от нормативного значения сцепления
грунта сн (см. п. 3.10)
по формуле
- усталостная прочность на разрыв
связного грунта, определяемая в зависимости от нормативного значения сцепления
грунта сн (см. п. 3.10)
по формуле
Для связных грунтов плотностью ρs = 2650 кг/м3 в потоках, свободных от наносов, Vн можно принимать по табл. 7 или по графику рис. 6 в зависимости от расчетного сцепления срасч = сн/Kс.
3.20. Для сложных связных грунтов, содержащих включения гравия, гальки или валунов, предельную неразмывающую скорость следует устанавливать в зависимости от количества включений и характера их залегания. Для грунтов, в которых связная часть лишь заполняет поры (пространство) между зернами гравия или гальки, значение Vн следует устанавливать как для несвязного грунта. При объеме включений не более 20 % или при их слоистом расположении расчет следует вести по основному грунту [48].
3.21. В предварительных расчетах и при отсутствии достаточных данных для расчета по формуле (25) значение Vн для связных грунтов может быть приближенно определено по ориентировочному описанию вида грунта, приводимому в табл. 7 в соответствии с данными, содержащимися в [46].
Связные грунты, характеризующиеся в водонасыщенном состоянии трещиноватостью, рассматриваются как несвязные, если сопротивляемость размыву отдельностей грунта не обусловливает назначение более низких неразмывающих скоростей по формуле (25). В этом случае неразмывающие скорости устанавливают по зависимостям для несвязных грунтов; за крупность частиц несвязного грунта принимают средний размер (приведенный диаметр, см. п. 3.7) отдельностей, окаймленных трещинами.
Для некоторых видов скальных и полускальных грунтов значения Vн предельных неразмывающих скоростей могут быть приняты по табл. 8, заимствованной из работы [46].
3.22. В инженерной практике устойчивость грунта против размыва часто оценивается не по значениям неразмывающей скорости Vн, а по предельному неразмывающему касательному напряжению на дне (или на смоченном периметре) потока [13]
![]() (27)
(27)
где ![]() - значение
динамической скорости, при которой грунт данного состава является предельно
устойчивым против размыва.
- значение
динамической скорости, при которой грунт данного состава является предельно
устойчивым против размыва.
Таблица 7
Неразмывающие скорости Vн для связных грунтов
|
Ориентировочное описание соответствующих видов связного грунта |
Расчетное сцепление срасч = сн/Kс кПа (т/мс2) |
Придонная скорость uд.н на высоте выступов шероховатости, м/с |
Средняя скорость Vн, м/с, при глубине потока h, м |
|||||||
|
супесь |
суглинок |
глины |
0,5 |
1 |
3 |
5 |
10 |
|||
|
малоплотная |
мало-плотный |
легкий |
0,5 |
0,16 |
0,39 |
0,43 |
0,49 |
0,52 |
0,56 |
|
|
тяжелый |
1,0 |
0,18 |
0,44 |
0,48 |
0,55 |
0,58 |
0,63 |
|||
|
2,0 |
0,21 |
0,52 |
0,57 |
0,65 |
0,69 |
0,74 |
||||
|
среднеплотная |
малоплотные |
3,0 |
0,24 |
0,59 |
0,64 |
0,74 |
0,78 |
0,84 |
||
|
4,0 |
0,27 |
0,65 |
0,71 |
0,81 |
0,86 |
0,92 |
||||
|
средне плотный |
легкий |
5,0 |
0,29 |
0,71 |
0,77 |
0,89 |
0,98 |
1,01 |
||
|
плотная |
тяжелый |
7,5 |
0,34 |
0,83 |
0,91 |
1,04 |
1,10 |
1,19 |
||
|
10,0 |
0,39 |
0,96 |
1,04 |
1,20 |
1,27 |
1,37 |
||||
|
плотный |
легкий |
среднеплотные (нормальные) |
12,5 |
0,42 |
1,03 |
1,13 |
1,30 |
1,37 |
1,47 |
|
|
тяжелый |
15,0 |
0,46 |
1,13 |
1,23 |
1,41 |
1,49 |
1,61 |
|||
|
17,5 |
0,50 |
1,21 |
1,33 |
1,52 |
1,60 |
1,72 |
||||
|
плотные |
20,0 |
0,53 |
1,26 |
1,40 |
1,60 |
1,69 |
1,82 |
|||
|
22,5 |
0,56 |
1,36 |
1,48 |
1,70 |
1,80 |
1,93 |
||||
|
25,0 |
0,58 |
1,42 |
1,55 |
1,78 |
1,88 |
2,02 |
||||
|
30,0 |
0,63 |
1,54 |
1,69 |
1,94 |
2,04 |
2,20 |
||||
|
35,0 |
0,69 |
1,67 |
1,83 |
2,09 |
2,21 |
2,38 |
||||
|
40,0 |
0,74 |
1,79 |
1,96 |
2,25 |
2,38 |
2,56 |
||||
|
45,0 |
0,77 |
1,88 |
2,06 |
7,35 |
7,49 |
2,64 |
||||
|
50,0 |
0,82 |
1,99 |
2,17 |
2,50 |
2,63 |
2,84 |
||||
|
60,0 |
0,89 |
2,16 |
2,38 |
2,72 |
2,88 |
3,10 |
||||
Рис. 6. Зависимость неразмывающих скоростей Vн связных грунтов от расчетного значения сцепления срасч = сн/Kc при плотности ρs = 2650 кг/м3 и коэффициенте mм = 1
Определение значения ![]() для несвязных
грунтов может быть выполнено
[22] по графику B.C. Кнороза
для несвязных
грунтов может быть выполнено
[22] по графику B.C. Кнороза  на рис. 7, где
на рис. 7, где  - коэффициент устойчивости донных
частиц.
- коэффициент устойчивости донных
частиц.
Переход от предельных значений динамической скорости (или касательного напряжения) к неразмывающей средней скорости Vн может быть осуществлен с помощью формулы Шези
 (28)
(28)
справедливой для равномерного или близкого к нему потока.
Таблица 8
Неразмывающие скорости Vн для полускальных и скальных грунтов
|
Средняя скорость Vн, м/с, при глубине потока h, м |
||||||
|
1 |
3 |
5 |
10 |
15 |
20 |
|
|
Алевролит слабый |
0,50 |
0,60 |
0,70 |
0,80 |
0,85 |
0,90 |
|
Алевролит средней крепости |
1,00 |
1,25 |
1,40 |
1,60 |
1,70 |
1,80 |
|
Алевролит крепкий |
1,50 |
1,90 |
2,05 |
2,40 |
2,60 |
2,70 |
|
Мергель |
2,50 |
3,00 |
3,45 |
3,95 |
4,30 |
4,55 |
|
Известняк пористый, слоистый и доломитовый |
3,50 |
4,40 |
4,85 |
5,50 |
6,00 |
6,35 |
|
Известняк плотный, неслоистый и кремнистый |
5,00 |
6,25 |
6,90 |
7,90 |
8,60 |
9,10 |
|
Песчаник известковый |
3,50 |
4,40 |
4,85 |
5,50 |
6,00 |
6,35 |
|
Песчаник доломитовый |
5,00 |
6,25 |
6,90 |
7,90 |
8,60 |
9,10 |
|
Гранит и другие изверженные кристаллические породы |
> 15 |
> 15 |
> 15 |
> 15 |
> 15 |
> 15 |
Рис. 7. График
изменения коэффициента подвижности ![]() донных частиц от параметра
донных частиц от параметра ![]() d/v по B.C. Кнорозу
d/v по B.C. Кнорозу
4. ОПРЕДЕЛЕНИЕ РАСХОДА РУСЛОФОРМИРУЮЩИХ НАНОСОВ
4.1. По участию в формировании речного русла наносы, перемещаемые потоком, условно делятся на руслоформирующие (русловые) и транзитные (нерусловые). К руслоформирующим относят фракции наносов, содержащиеся в донных отложениях [11, 44, 47]. Мелкие фракции (обычно d < 0,05 мм), переносимые потоком на значительные расстояния и не встречающиеся в больших количествах в донных отложениях, относят к транзитным наносам. Большая часть транзитных наносов переносится потоком без осаждения, но некоторая их часть осаждается в зонах с малыми скоростями течения, формируя верхние горизонты пойм и островов.
4.2. По форме движения наносы делятся на влекомые (донные) и взвешенные. Влекомые наносы перемещаются скольжением, перекатыванием или сальтацией (скачками) по дну или вблизи дна в слое, толщина которого соизмерима с размером частиц, и всегда являются руслоформирующими. Взвешенные наносы перемещаются во взвешенном состоянии в слое, толщина которого соизмерима с глубиной потока или равна ей, и могут быть как руслоформирующими, так и транзитными.
4.3. На основе данных натурных наблюдений за твердым стоком определяется форма движения наносов при однородном грунте, зная которую можно определить транспортирующую способность потока (п. 4.10). При разнородном грунте часть наносов может перемещаться во влекомом состоянии, а часть во взвешенном. При этом в формировании русла целиком участвуют влекомые наносы и частично - взвешенные, значительная доля которых на спаде паводка может перейти во влекомое состояние и отложиться на дне. В связи с этим одной из задач расчета становится нахождение доли руслообразующих фракций kрф в составе взвешенных наносов (п. 4.5).
Определение формы движения наносов может быть ориентировочно осуществлено также на основании данных о гранулометрии донных отложений путем сопоставления гидравлической крупности частиц рассматриваемой фракции с параметрами потока [60]:
частицы на дне неподвижны
и*/w < (0,16 - 0,25) - в соответствии с зависимостью (7) и графиком рис. 7;
частицы движутся по дну
(0,16 - 0,25) < u*/w < (0,5 - 0,8); (29)
сальтация
0,8 < u*/w < 1,7;
взвешивание и образование суспензии
1,7 < u*/w,
где u* - динамическая скорость потока, определяемая в зависимости от средних его характеристик
4.4. При наличии данных гидрометрических
измерений стока взвешенных наносов в бытовых условиях на расчетном участке
нижнего бьефа расход наносов Qs следует определять по методу К.И. Российского и И.А. Кузьмина [45]. Метод основан на использовании
установленной М.А. Великановым зависимости концентрации наносов от параметра ![]() В
предположении малого изменения средней гидравлической крупности взвешенных
наносов в пределах исследуемого бьефа строится зависимость
В
предположении малого изменения средней гидравлической крупности взвешенных
наносов в пределах исследуемого бьефа строится зависимость
где S - средняя концентрация руслоформирующих фракций наносов в потоке; w - их средняя гидравлическая крупность; V и h - средняя скорость и глубина потока в створе измерений.
Как правило, зависимость (31) представляет собой поле точек, ограниченных двумя кривыми, нижняя из которых трактуется как ветвь размыва, а верхняя - как ветвь отложений. Связь (31) предполагается справедливой в качественном отношении и для зарегулированного русла.
Поле точек, ограниченное двумя огибающими, можно толковать и как отражение различной степени насыщения потока наносами при различных условиях (на подъеме и спаде паводка, при различной интенсивности нарастания и спада уровней, в межень и т.п.).
В этом случае верхняя огибающая характеризует транспортирующую способность потока (то есть полное насыщение потока наносами Qs = Ps), а нижняя - расход наносов (вернее, концентрацию S), соответствующий размывающей способности потока при Qs << Ps.
При недостаточности данных наблюдений построение кривых, ограничивающих поле точек (31), можно производить по формулам:
где b = 23,7 ∙ 10-5ρw/ρs и a = 4,75 ∙ 10-5ρw/ρs.
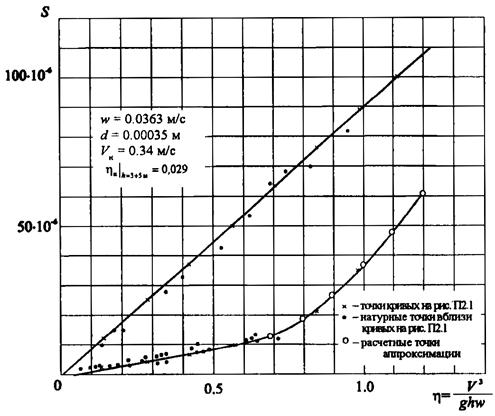
В общем случае значения гидравлической крупности в зависимостях (32) и (33) должны отличаться между собой. Причем можно полагать, что wверхн < wнижн, но если данных о гидравлической крупности недостаточно, то можно принять wверхн = wнижн = w. При таком предположении значение w может быть определено с помощью следующего приема. Построив по данным измерений поле точек в координатах S и V3/h, можно провести верхнюю огибающую (она, как правило, более надежна) и аппроксимировать ее линейной зависимостью S = kBV3/h (Приложение 2, рис. П2.1), что можно сделать практически всегда. Приравняв затем эту аппроксимацию выражению (32), легко найти
![]()
по w можно определить и среднюю крупность наносов.
После этого поле точек
перестраивается в координатах (31).
Для верхней огибающей принимается связь (32), а нижняя огибающая аппроксимируется зависимостью
вида Sнижн = a(η - ηн)α, где в общем случае α ≠ 1, a ![]() (Приложение
2, рис. П2.2).
(Приложение
2, рис. П2.2).
В процессе деформации русла может происходить изменение состава грунта в отложениях и, следовательно, их гидравлической крупности. Происходящее при этом изменение кривых S = f(η) следует, по мере возможности, учитывать путем их перестройки. Для этого значения S должны быть пересчитаны пропорционально отношению первоначальной гидравлической крупности к изменившейся: Sи = Sпwп/wи (индекс «п» соответствует первоначальным, то есть бытовым, условиям, индекс «и» - изменившимся).
4.5. Содержание руслоформирующих фракций взвешенных наносов составляет некоторую долю kрф от общей мутности Sобщ потока. Выделение руслоформирующих фракций производится сопоставлением гранулометрических составов взвешенных наносов и донных отложений на основании гидрометрических измерений и определяется как отношение расхода руслоформирующих фракций к полному расходу взвешенных наносов. Приближенно значение kрф можно принимать равным среднему содержанию руслоформирующих фракций в составе взвешенных наносов
где K, J - число вертикалей (k) и точек на них (j), в которых производился отбор проб наносов; ррф - процентное содержание руслоформирующей фракции в данной точке.
4.6. Расход взвешенных наносов определяется по формуле
Qs = SQ, (35)
где S - концентрация руслоформирующих фракций наносов в потоке.
4.7. При отсутствии гидрометрических измерений стока взвешенных наносов или при их ограниченности и отрывочности не существует достаточно общих методов определения расхода наносов Qs. В этом случае можно воспользоваться одной из формул транспортирующей способности потока Ps (см. п. 4.10), для которой будет достаточной имеющаяся информация и область применения которой соответствует заданным условиям. При наличии отрывочных гидрометрических измерений следует проверить, насколько удачно они аппроксимируются принятой зависимостью транспортирующей способности потока, имея в виду, что для взвешенных наносов она должна являться верхней огибающей поля точек. При этом нижняя огибающая может быть принята из условия
Sнижн = 0,2Sверхн, (36)
которое вытекает из сопоставления (32) и (33).
4.8. Расход Qs влекомых наносов определяется по данным натурных наблюдений, а при их отсутствии или ограниченности, как и в случае взвешенных наносов, - по одной из формул транспортирующей способности Ps (см. п. 4.10), для которой будет достаточной имеющаяся информация и область применения которой соответствует заданным условиям.
4.9. При отсутствии гидрометрических данных расход наносов в расчетных створах определяется исходя из вычисленных значений транспортирующей Ps и размывающей Рр способностей потока по геометрическим характеристикам русла, физико-механическим характеристикам материала донных отложений и переносимых потоком наносов.
4.10. Определение транспортирующей способности потока при расчете трансформации русла может производиться по одной из формул, целесообразность применения которых оправдывается имеющимся опытом расчетов.
1) Формула И.И. Леви [28, 29] для влекомых наносов (u*/w < 0,8), применимая при d/h > 1/5000:
а) для однозернистых грунтов
б) для разнозернистых грунтов [39]
где Vнj - предельная неразмывающая скорость для j-ой фракции грунта крупностью dj.
2) Транспортирующая способность потока при движении влекомых наносов (и*/w < 0,8) может быть определена также по элементам движения гряд, исходя из зависимости [12]
Ps = (1 - δ)σcгhгB, (39)
где σ - коэффициент полноты гряд, численное значение которого изменяется в зависимости от формы гряд в пределах от 0,5 до 0,75 и при отсутствии данных специальных исследований может быть принято равным ≈ 0,6; hг - высота гряды, определяемая по формуле В.С. Кнороза [23]
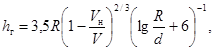 (40)
(40)
где R - гидравлический радиус потока; сг - скорость движения гряд, определяемая по формуле В.С. Кнороза [23]
 (41)
(41)
или по формуле Б.Ф. Снищенко - З.Д. Копалиани [50]*
 (42)
(42)
_____________
* Имеется также предложение Н.И. Алексеевского [1], позволяющее определять сг в зависимости от типа донных гряд и порядка водотока (по Н.А. Ржаницыну, 1980, или Хортону, 1948), а также вносящее некоторые уточнения, учитывающие форму гряд разного типа.
Формулы В. С. Кнороза применимы при V < (2,5 - 2,7)Vн.
3) Формула А.В. Караушева [18, 19] для взвешенных наносов крупностью 0,04 ≤ d ≤ 0,3 мм (0,0009 ≤ wср ≤ 0,02 м/с), характеризующихся отношением и*/w > 1,7,
где ![]() - средняя
гидравлическая крупность транспортируемых потоком фракций; m - число транспортируемых фракций; pj - процентное
содержание j-ой фракции с гидравлической крупностью wj.
- средняя
гидравлическая крупность транспортируемых потоком фракций; m - число транспортируемых фракций; pj - процентное
содержание j-ой фракции с гидравлической крупностью wj.
4) Формула В.Н. Гончарова [11] для влекомых и взвешенных наносов (u*/w < 2,5)
где φ - параметр, определяемый по формуле
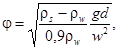
w - средняя гидравлическая крупность наносов.
Область применения формулы В.Н. Гончарова обоснована опытами при условиях: 10 ≤ h/d ≤ 1550 (8,7 ≤ h/d95 ≤ 500); 1 ≤ V/Vн ≤ 1,8.
При V/Vн > 2 можно пользоваться упрощенной зависимостью
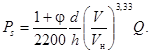 (45)
(45)
5) Формула Р.А. Бэгнольда для влекомых и взвешенных наносов [61]
где ![]() φ - угол внутреннего трения грунта ложа
реки; α - угол наклона дна к горизонту; w - гидравлическая крупность
наносов; Сf - коэффициент трения, вычисляемый по зависимости
φ - угол внутреннего трения грунта ложа
реки; α - угол наклона дна к горизонту; w - гидравлическая крупность
наносов; Сf - коэффициент трения, вычисляемый по зависимости
 (47)
(47)
где k
- постоянная Кармана; Δ - эффективная высота выступов шероховатости, принимаемая в
зависимости от значения параметра ![]()
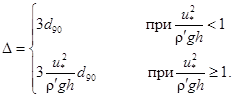
Первый член в скобках в формуле (46) учитывает долю влекомых наносов, а второй - взвешенных.
Необходимое условие применимости формулы Р.А. Бэгнольда для влекомых наносов α < φ выполняется, как правило, автоматически, поскольку диапазон изменения tgφ составляет 0,4 < tgφ < 0,75, a tgα редко (лишь в верховьях горных рек) превосходит 0,1. Для взвешенных наносов условие ее применимости tgα < w/V должно проверяться, но поскольку чем больше уклон дна и скорость потока, тем более крупные частицы грунта переходят во взвешенное состояние, это условие тоже будет выполняться в достаточно широком диапазоне.
4.11. Допущение Qs = Ps (пп. 4.7 - 4.9) не приводит к значительным ошибкам при расчетах деформации русла незарегулированных рек и участков нижних бьефов, удаленных от гидроузла на большие расстояния.
Для участков нижних бьефов,
прилегающих к гидроузлу или к зоне осветленного потока, помимо зависимости для
определения Ps должна быть принята связь между степенью насыщения потока Qs/Ps и относительной интенсивностью размыва русла ![]()
отражающая уменьшение
интенсивности размыва от значения ![]() при Qs = 0 до
при Qs = 0 до ![]() при Qs → Ps, где Рр - размывающая способность потока, то есть
количество грунта, снимаемого потоком с единицы площади дна в единицу времени,
м/с [53].
при Qs → Ps, где Рр - размывающая способность потока, то есть
количество грунта, снимаемого потоком с единицы площади дна в единицу времени,
м/с [53].
4.12. При размыве несвязного грунта осветленным потоком размывающая способность Рр определяется по формуле В.М. Доненберга [16]
обоснованной опытами при 1 < V/Vн ≤ 3; d/h > 0,01 для грунтов крупностью 0,1 ≤ d ≤ 1 мм и d/h > 0,025 - для грунтов крупностью d > 1 мм. Коэффициенты А и показатели степени т вычисляются по зависимостям:
А = Сs ∙ 10-9, (50)
![]() (51)
(51)
где ![]() гидравлическая крупность w определяется по данным п. 3.11.
гидравлическая крупность w определяется по данным п. 3.11.
4.13. При размыве русла, сложенного связными грунтами, размывающая способность потока определяется по формуле Ц.Е. Мирцхулавы [35, 36]
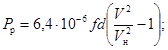 (52)
(52)
где f - средняя частота пульсации донной скорости; в первом приближении может быть принята равной f = 0,73V/h [37]; d - приведенный диаметр отдельностей связного грунта, который при отсутствии данных специальных исследований принимается равным 0,004 м.
5. ГИДРАВЛИЧЕСКИЕ ХАРАКТЕРИСТИКИ РЕЧНЫХ ПОТОКОВ
Назначение расчетных расходов воды
5.1. При детальных расчетах трансформации русла нижнего бьефа в качестве аналога принимается некоторая последовательность чередования гидрографов длительного многолетнего периода, в которую взамен наблюденных включаются расчетные зарегулированные гидрографы многоводного, маловодного и среднего по водности года. Расчеты могут быть проведены также для различных вариантов последовательности пропуска зарегулированных гидрографов.
Расчетные гидрографы могут быть схематизированы ступенями различной продолжительности Δt с постоянным расходом Q.
5.2. При расчетах по приближенному методу (пп. 6.28 - 6.31) в качестве расчетного расхода воды следует принимать руслоформирующий расход Qрф, соответствующий среднемноголетнему расходу наносов (этот расход принимается по данным многолетних гидрометрических наблюдений), а продолжительность расчетного года - равной средней продолжительности зарегулированного паводка. Допустимым является принятие Qрф равным максимальному расходу, при котором речной поток находится в бровках меженного русла.
При расчетах на предельное состояние размыва во многих случаях в качестве расчетного может быть принят расход, обусловивший назначение пропускной способности гидроузла при нормальных условиях его эксплуатации, то есть максимальный расход заданной обеспеченности в соответствии со СП 33-101-2003 в зависимости от класса сооружений гидроузла (по СНиП 33-01-2003).
Схематизация речных русел
5.3. В качестве исходных данных для схематизации речного русла при расчетах его трансформации в нижних бьефах гидроузлов должны использоваться следующие материалы:
план рассчитываемого участка русла и поймы в горизонталях (или достаточно частые поперечные профили русла) на начальный момент расчета;
продольные профили дна русла и коренных неразмываемых пород;
кривые расходов Q = f(H) в имеющихся гидростворах;
данные о механическом составе и физических свойствах грунтов, слагающих русло, пойму и берега.
5.4. Приведенные в пп. 5.5 - 5.19 принципы схематизации речного русла относятся, главным образом, к расчетам, выполняемым в рамках одномерной идеализации руслового потока (см. гл. 6). При составлении прогноза трансформации русла в нижних бьефах, когда расчетом должны быть охвачены участки реки значительной протяженности, многократно превышающие ширину потока, такая расчетная модель является оправданной. В тех случаях, когда для уточнения результатов расчетов одномерной модели необходимо дать оценку русловых переформирований на отдельных участках ограниченной протяженности с дифференциацией по ширине русла слоя деформации, следует использовать двухмерную плановую модель руслового потока. Схематизация исходных параметров русла в этом случае сводится, по существу, к назначению плановых координат узлов расчетной сетки и отметок дна в этих точках (см. гл. 7), то есть существенно упрощается по сравнению со схематизацией, которая должна быть выполнена для расчетов одномерной модели.
5.5. По имеющемуся плановому материалу русло разбивается по длине на участки так, чтобы в пределах одного участка ширина русла в бровках изменялась по возможности не более, чем на 10 - 20 %.
В соответствии с продольным профилем (пп. 5.12 - 5.14) каждый большой участок может быть дополнительно разбит на более мелкие расчетные участки, в пределах которых средние глубины потока при минимальном расчетном расходе воды не должны отклоняться друг от друга более, чем на 20 - 30 %.
5.6. При использовании в расчетах допущения Qs = Ps длина ближайших к гидроузлу расчетных участков должна быть порядка 2 - 3 ширин русла. По мере удаления от гидроузла протяженность участков может увеличиваться. При учете постепенности насыщения по зависимости (48) длина расчетных участков может назначаться произвольно.
5.7. При разбивке русла на участки желательно, чтобы их граничные створы были приурочены к гидростворам или водомерным постам, а также к местам впадения притоков, расходами которых нельзя пренебречь по сравнению с расходами главной реки. Места выходов скальных пород должны быть выделены в отдельные участки.
5.8. В пределах участка должно соблюдаться однообразие характеристик грунта. Помимо одинаковости вида грунта (см. пп. 3.1 - 3.8), признаками однообразия следует считать незначительное изменение (до 20 %) средней крупности грунта d, коэффициента разнозернистости d95/d5, связности с, плотности материала наносов ρs и грунта ρгр.
5.9. Поперечные сечения расчетного русла могут быть для удобства расчета схематизированы в виде трапеции, параболы, прямоугольника, их сочетания и т.д. При схематизации поперечных сечений в различных створах (как граничных, так и промежуточных) необходимо, чтобы зависимость площади живого сечения от уровня воды в действительном и схематизированном русле во всем диапазоне изменения Н приближенно соответствовали друг другу. Для расчетов трансформации русла в нижних бьефах чаще всего применяется и может считаться достаточной простейшая схематизация поперечных сечений прямоугольником или сочетанием нескольких прямоугольников.
5.10. В общем случае ширина русла по урезу и глубина потока являются нелинейными функциями расхода воды: B = B(Q) и h = h(Q). Поскольку
h = y - z (y ≡ H), (53)
отметка дна зависит от расхода
z = y(Q) - h(Q) = z(Q). (54)
При подборе формы
схематизированного поперечного сечения критерием удачного подбора следует
считать небольшой (до 10 %) разброс значений z(Q). Среднюю отметку дна схематизированного сечения русла в этом случае
можно принимать как среднеарифметическое ![]() из интервала [zмин; zмакс].
из интервала [zмин; zмакс].
5.11. В ряде случаев при схематизации поперечного сечения прямоугольником удобным является следующий прием определения геометрических характеристик схематизированного сечения русла.
Ширина фиктивного прямоугольного русла принимается равной
![]() (55)
(55)
где ω(Qмакс) и умакс - площадь живого сечения и отметка свободной поверхности при максимальном расчетном зарегулированном расходе воды Qмакс; ω(Qмин) и умин - то же при минимальном расчетном зарегулированном расходе воды Qмин.
Отметка дна z в этом случае является постоянной для данного сечения (рис. 8):
![]() (56)
(56)
При выходе воды на пойму значения ω при различных расходах должны приниматься равными условным значениям, характеризующим сечение руслового потока, ограниченного со стороны поймы бровкой (или бровками при двухстороннем расположении поймы) меженного русла.
Рис. 8. Схематизация живого сечения потока
5.12. Определенные согласно пп. 5.10 - 5.11 средние отметки дна z поперечных сечений являются основой для построения схематизированного продольного профиля дна.
По этим данным в пределах каждого расчетного участка (см. пп. 5.5 - 5.8) проводится осредненная линия дна.
5.13. В зависимости от используемого метода расчета трансформации русла схематизированный продольный профиль дна (рис. 9) может назначаться:
ступенчатым или в виде ломаной линии со ступенями или изломами в расчетных створах - при выполнении подробных расчетов с разбивкой бьефа на участки;
линейным - при выполнении расчетов приближенным методом.
Рис. 9. Схематизация продольного профиля дна:
1 - ступенчатый; 2 - в виде ломаной линии; 3 - линейный
5.14. При ограниченной информации о топографии русла для построения схематизированного продольного профиля могут использоваться имеющиеся данные о кривых расходов в различных створах расчетного участка. В гидростворах - это результаты непосредственных измерений, а на водпостах и в промежуточных створах - кривые, построенные переносом по связи уровней или по интерполяции.
Определение отметки дна схематизированного русла по кривой Q = f(H) в рассматриваемом створе основывается на допущении справедливости показательной зависимости
где æ - гидравлический показатель русла. В зависимости от формы русла численное значение его изменяется в диапазоне от æ = 2,0 (узкие прямоугольные русла) до æ = 5,4 (треугольные русла).
Исходя из формулы (57), кривые Q = f(H) перестраиваются в виде прямых (рис. 10)
Q2/æ = k1(H - z), (58)
где ![]() - угловой
коэффициент прямой на рис. 10.
- угловой
коэффициент прямой на рис. 10.
Рис. 10. Схема к определению расчетных отметок дна по кривым связи Q = f(H):
![]() - Q2/æ = f(H);
- Q2/æ = f(H); ![]() Q2/æ = k1(H - z)
Q2/æ = k1(H - z)
При этом неизвестные
параметры æ, k1 и z определяются либо подбором, либо методом выравнивающих: по
произвольным значениям Q1 и Q2 и значению ![]() находятся
соответствующие им H1, H2 и H3 и далее
вычисляются в первом приближении
находятся
соответствующие им H1, H2 и H3 и далее
вычисляются в первом приближении ![]() , затем по произвольным узловым точкам [Q, H] строится логарифмическая
анаморфоза lgQ = f[lg(H - z)], на которой исходная зависимость Q
= f(H) представляется в виде прямой
, затем по произвольным узловым точкам [Q, H] строится логарифмическая
анаморфоза lgQ = f[lg(H - z)], на которой исходная зависимость Q
= f(H) представляется в виде прямой ![]() и по ней определяются k1 и æ; по полученным их следует уточнить z, приняв его равным среднему из значений
и по ней определяются k1 и æ; по полученным их следует уточнить z, приняв его равным среднему из значений ![]() , охватывающих
весь диапазон изменения расходов.
, охватывающих
весь диапазон изменения расходов.
Для естественных широких
речных русел можно, как правило, принимать æ = 4,0. В этом случае определение æ существенно облегчается и вместо построения графика ![]() (рис. 10)
ограничивается непосредственным преобразованием известной зависимости Q = f(H)
в зависимость
(рис. 10)
ограничивается непосредственным преобразованием известной зависимости Q = f(H)
в зависимость ![]() , по
которой и находится z, равное
значению H
при Q = 0.
, по
которой и находится z, равное
значению H
при Q = 0.
Пример использования приемов, описанных в пп. 5.7 - 5.14, представлен в Приложении 1.
5.15. При отсутствии данных натурных наблюдений для створов, расположенных в пределах прямолинейных или слабоизогнутых плесовых лощин, зависимость расходов воды Q от уровней Н = z + h может быть построена по формуле К.В. Гришанина [13]
где h = ω/В; ω - площадь живого сечения реки в рассматриваемом створе при заданном уровне свободной поверхности Н; В - ширина потока по верху при том же уровне.
Значение коэффициента М - инварианта подобия квазиравномерных потоков [13] - для русел, сложенных несвязными грунтами, может быть приближенно определено по формуле
![]() (60)
(60)
В руслах, сложенных песком или мелким гравием, М = 0,92 ± 0,12, и с достаточной для практики точностью можно округленно принимать М = 0,9. Для плесовых лощин в галечно-валунном грунте значения М уменьшаются до 0,5 - 0,6.
Если в створе, расположенном в пределах плесовой лощины, имеются измерения 2 - 3-х расходов воды, то значения М целесообразно по этим расходам скорректировать.
Изложенный способ построения кривых Q = f(H) справедлив только для плесовых лощин с незатопляемыми берегами. Поэтому с помощью зависимости (59) может быть построена лишь нижняя часть кривой для русла в бровках. При выходе же потока на пойму зависимость (59) неприменима.
Зависимость (59) является частным случаем зависимости (58) при æ = 4,0. Преимуществом же зависимости (59) в области ее применимости является непосредственное выражение расхода через геометрические характеристики сечения, что позволяет использовать ее для интерполяции кривых Q = f(H) в промежуточных створах участка, включающего плесовые лощины.
5.16. На схематизированный продольный профиль дна наносится по данным геологических изысканий продольный профиль коренных неразмываемых пород. Разница между отметками этих профилей дает толщину деформируемого аллювиального слоя.
Если в составе аллювия встречаются слои крупнозернистого или другого грунта, для которого неразмывающие скорости превышают скорости потока, поверхность залегания этих грунтов следует считать неразмываемой при заданных расходах и глубинах потока.
Гидравлические сопротивления
5.17. Потери энергии вычисляются по зависимостям равномерного движения [54, 55], причем все потери на участке относятся на счет сопротивлений по длине потока. Тогда:
где чертой сверху отмечены средние характеристики потока и русла на участке; m - показатель степени, для естественных русел принимаемый обычно по Маннингу равным 1/6.
5.18. Коэффициенты шероховатости nш вычисляются по имеющимся исходным данным и в соответствии с выполненной схематизацией для ряда расходов воды в схематизированном исходном русле по уравнению неравномерного движения [54]
откуда с учетом (61) и (62) при m = 1/6
где k - номер участка и его низового створа.
5.19. В тех случаях, когда между гидростворами (или водпостами), для которых имеются кривые связи расходов и уровней, выделены несколько расчетных участков с различными геометрическими и гидравлическими характеристиками русла, коэффициенты шероховатости nш для этих участков (и кривые Q = f(H) в их граничных створах) целесообразно устанавливать подбором, проводя расчет кривых свободной поверхности от одного гидроствора с заданной зависимостью Q = f(H) до другого. Если при выполнении такого расчета изменение скоростного напора в уравнении (63) оказывается пренебрежимо малым, то
yk-1 - yk = ifΔxk. (65)
Расчет сводится к следующим операциям:
1) в соответствии с табл. 9 или другими рекомендациями, имеющимися в специальной литературе (см., например, [54]), назначаются в первом приближении значения nш - различные для каждого участка или одинаковые для всех участков;
2) для каждого участка по формуле (61) вычисляются if и последовательно от створа к створу (обычно вверх по течению) определяются по уравнению (65) отметки yk свободной поверхности;
3) для створов с известной кривой расходов производится сравнение вычисленной и заданной отметок свободной поверхности;
4) полученная невязка распределяется между участками пропорционально их длинам, и принятые значения корректируются;
5) в том случае, когда по соображениям удобства расчета целесообразно иметь одинаковые на всех участках значения nш, вычисляется среднее из скорректированных значений nш, и расчет повторяется до тех пор, пока расхождение в падении уровней между створами с заданными кривыми Q = f(H) не окажется менее 1 %.
Таблица 9
Коэффициент шероховатости для естественных водотоков [55]
|
Значения nщ |
|||
|
минимальные |
средние |
максимальные |
|
|
Большие потоки (правильные поперечные сечения русла; кустарников и валунов нет) |
0,025 |
- |
0,060 |
|
Русла с поймой |
|||
|
пойма без кустарников и деревьев |
0,025 |
- |
0,050 |
|
пойма, покрытая кустарником |
0,035 |
- |
0,160 |
|
пойма, покрытая деревьями |
0,110 |
- |
0,200 |
|
Малые потоки шириной менее 30 м |
|||
|
равнинные |
0,025 |
0,070 |
0,150 |
|
горные |
0,030 |
0,045 |
0,070 |
5.20. На основании вычисленных по уравнению (64) значений строятся графические или табличные зависимости nш = nш(Q) для каждого расчетного участка исходного русла, которые затем распространяются и на русло в процессе его размыва.
6. РАСЧЕТ ТРАНСФОРМАЦИИ РУСЛА В НИЖНЕМ БЬЕФЕ
Общие принципы расчета
6.1. Течения в деформируемых руслах являются неустановившимися, поэтому расчет трансформации русла в нижнем бьефе гидроузла должен проводиться на основе совместного решения системы следующих уравнений, учитывающих нестационарность потока: уравнений движения и неразрывности воды; уравнений движения и баланса массы наносов; уравнения деформации русла. В наиболее полном виде эта система весьма громоздка и решение ее представляет серьезные трудности. С достаточной для практических расчетов точностью может быть использована упрощенная система, справедливая для неустановившихся русловых потоков, насыщение которых наносами характеризуется концентрацией, не превышающей 1 - 1,5 % [3, 4]:
уравнение движения
уравнение неразрывности воды
![]() (67)
(67)
уравнение баланса массы наносов
![]() (68)
(68)
уравнение деформации русла
где qs - приходящийся на единицу длины потока расход притока (или оттока) наносов, происходящего в процессе массообмена потока и русла при русловых переформированиях.
6.2. В качестве дополнительных связей к
системе (66)
- (69) должны быть привлечены зависимости
для определения уклона потерь энергии на трение if, расхода наносов Qs и интенсивности береговых деформаций ![]()
Уклон трения if допустимо определять по зависимости Шези-Маннинга (61) - (62) или другим аналогичным формулам.
Определение расхода наносов Qs в общем виде может быть осуществлено по зависимости (48), конкретное выражение которой
подлежит специальным исследованиям. В первом приближении, принимая ![]() и
пренебрегая береговыми деформациями русла по сравнению с деформациями дна
и
пренебрегая береговыми деформациями русла по сравнению с деформациями дна ![]() , для
определения Qs может быть использована обобщенная гипотеза Г.Р. Фостера и
Л.Д. Мейера [56]:
, для
определения Qs может быть использована обобщенная гипотеза Г.Р. Фостера и
Л.Д. Мейера [56]:
где показатель степени m для условий руслового потока в нижних бьефах гидроузлов может быть принят равным 4 - 5*.
_____________
* Г.Р. Фостер и Л.Д. Мейер [56], исследовавшие склоновую эрозию почвы, принимали m = 1.
В случае, когда береговыми
деформациями пренебречь нельзя, в зависимости (70) слева вместо ![]() должно быть
должно быть  где значение
где значение ![]() - определяется по п. 6.19.
- определяется по п. 6.19.
6.3. При решении системы уравнений (66) - (69), дополненной недостающими связями (п. 6.2), в качестве начальных условий (при t = 0) должны быть заданы применительно к условиям задачи геометрические и гидравлические характеристики руслового потока в соответствии с их схематизацией (пп. 5.3 - 5.16) на всей исследуемой длине русла.
6.4. Необходимыми граничными условиями в начальном створе (z = 0) должны быть гидрографы жидкого и твердого стока. При расчетах деформаций русла, стесненного сооружениями (например, перемычками), расход наносов в начальном створе сужения** предполагается равным бытовому расходу наносов. При расчетах деформаций русла в нижнем бьефе концентрация наносов S (или расход наносов Qs) в створе гидроузла принимается по данным расчета осветления потока водохранилищем [52]; для случая полного осветления следует считать S = 0 (или Qs = 0).
_____________
** Этот створ следует принимать в месте выклинивания подпора, обусловленного стеснением русла.
Назначение расчетных расходов воды производится в соответствии с пп. 5.1 - 5.2.
6.5. В качестве граничного условия в низовом створе, ниже которого трансформация русла предполагается пренебрежимо малой, принимается бытовая связь расходов и уровней воды Q = f(H). Местоположение низового створа, которым ограничивается расчетная длина исследуемого бьефа, может уточняться в процессе расчета.
6.6. Расчеты на основе системы (66) - (69) целесообразно осуществлять при решении задач русловых деформаций под действием быстро изменяющихся неустановившихся течений (в том числе, волны прорыва).
6.7. В большинстве случаев русловые потоки могут рассматриваться как медленно изменяющиеся; при проведении расчетов такие потоки представляются в виде квазистационарных течений на каждом временном шаге продолжительностью Δt, и система расчетных уравнений существенно упрощается за счет исключения членов, учитывающих нестационарность течений. Упрощенная система, справедливая на каждом временном шаге, включает в себя:
уравнение движения (уравнение Бернулли)
уравнение неразрывности воды
Q = const; (72)
уравнение баланса массы наносов и деформации русла
В случаях, когда мощность слоя размываемого грунта незначительна и процесс размыва протекает относительно быстро, расчет целесообразно вести на условно предельное состояние для принятой длины распространения зоны размыва.
Эти случаи лежат в основе упрощенных приемов, применение которых в условиях недостаточного, как правило, обеспечения исходными данными, является оправданным.
Деформации русла в строительный период
6.8. Деформация русла на участке стеснения его перемычками или недостроенными сооружениями, а также на участке его последующего расширения может быть обоснованно рассчитана по двумерной (плановой) модели (см. гл. 7).
Приближенная оценка может быть выполнена по уравнениям (71) - (73) с использованием приемов, изложенных в пп. 6.15 - 6.27, в предположении, что расход наносов, поступающих в начальный створ стеснения, равен расходу наносов в бытовых условиях (см. п. 6.4)
Qsс = Qsб, (74)
где индексы «б» и «с» соответствуют бытовому и стесненному состояниям русла. Предварительно необходимо представить тем или иным методом [27, 28] план течения и очертить границы транзитного потока. При таком подходе деформации строительного периода будут рассматриваться как начальная фаза единого непрерывного процесса трансформации русла в нижнем бьефе в соответствии с описанием его в пп. 2.2 - 2.11.
6.9. Приближенная оценка деформации русла на участке стеснения может быть получена расчетом на предельное состояние. В основе расчета лежит предположение, что размыв стесненного русла протекает достаточно быстро и прекращается при скоростях, незначительно превышающих бытовые, при сохранении на всем участке сужения расхода наносов, равного бытовому [29, 51], то есть при соблюдении условия (74).
6.10. При использовании для Qs формулы (37) зависимость между параметрами размытого стесненного русла и русла в бытовом состоянии зависит от отношения расходов воды Qc и Qб и оценивается приближенным соотношением [28]
(hc/hб)4,25(Bc/Bб) = (Qc/Qб)4. (75)
Если русло реки на значительную глубину сложено однородными размываемыми грунтами, берега прочные и не подвергаются размыву, глубина размыва дна Δz = hс - hб определяется из (75):
а) в случае, когда поймы перекрыты и происходит слив пойменных вод в русло (Qс ≠ Qб),
![]() (76)
(76)
б) при отсутствии стеснения пойм или при уровнях воды ниже бровки русла (Qс = Qб)
6.11. Если русло реки сложено малоразмываемыми грунтами, а берега легко размываемыми (песок, супесь), сечение потока будет расширяться за счет размыва берегов
![]() (78)
(78)
6.12. Если на некоторой глубине в русле реки
залегают грунты, более устойчивые против размывов, чем в верхних слоях, а
берега русла неразмываемы, размыв русла прекращается при глубинах ![]() соответствующих
неразмывающим скоростям для этих грунтов (пп. 3.14 - 3.21).
соответствующих
неразмывающим скоростям для этих грунтов (пп. 3.14 - 3.21).
6.13. В случае, когда при ограниченности слоя размываемых донных отложений берега легко размываемы, сначала определяется hр (по п. 6.12), а затем
ΔB = Bб[(Qc/Qб)1,33(hб/hp)1,42 - 1]. (79)
6.14. Изложенные в пп. 6.8 - 6.13 приемы расчета дают представление о средней по сечению глубине размыва. Распределение глубин размыва по ширине потока В может быть уточнено на основании решения плановой задачи гидравлики и учета неоднородности геологического строения русла
Общие деформации русла нижнего бьефа
6.15. Расчет деформации на каждом расчетном участке исследуемого бьефа ведется конечно-разностным (балансовым) методом по уравнению (73), представленному в виде
При пренебрежимо малом размыве берегов (ΔB/Δt ≈ 0) уравнение (80) упрощается:
![]() (81)
(81)
6.16. В качестве начальных условий, то есть исходного состояния исследуемого русла, принимается схематизированное (пп. 5.3 - 5.16) бытовое русло с наложенными на него прогнозируемыми деформациями строительного периода и, при наличии данных специального расчета или лабораторных исследований, местными деформациями первых лет эксплуатации за водопропускными сооружениями.
6.17. Определение твердого расхода в створах, ограничивающих расчетные участки, при отсутствии или ограниченности данных натурных наблюдений производится по формуле (70), в которой Рs вычисляется по одной из формул п. 4.10, а Рp - по формуле (49); в створе гидроузла расход наносов принимается в соответствии с п. 6.4.
Транспортирующая Рs и размывающая Рp способности потока при известном составе донных отложений
определяются по их средней крупности ![]() где N - количество интервалов, на которое разбита кривая
гранулометрического состава; j - номер
интервала; dj - средний диаметр грунта j-го
интервала, характеризующегося процентным содержанием Δрj.
где N - количество интервалов, на которое разбита кривая
гранулометрического состава; j - номер
интервала; dj - средний диаметр грунта j-го
интервала, характеризующегося процентным содержанием Δрj.
6.18. Для потоков, характеризующихся движением
наносов во взвешенном состоянии, определение твердого расхода при наличии
данных натурных наблюдений производится последовательно сверху вниз по течению
по графику S = f(η) (п. 4.4), исходя из соотношения значений параметра ![]() на двух рядом расположенных
створах, руководствуясь следующими основными положениями [45]:
на двух рядом расположенных
створах, руководствуясь следующими основными положениями [45]:
а) Если параметр η в рассматриваемом створе k оказывается меньше такового для вышерасположенного створа (k - 1),
то есть ηk < ηk-1, то S определяется по верхней кривой, так как в этом случае следует
ожидать осаждения наносов (рис. 11,
а). Однако если при этом оказывается, что концентрация ![]() , определенная
по верхней кривой, получается больше, чем в вышерасположенном створе Sk-1, то уменьшение параметра η считается недостаточным для того, чтобы вызвать выпадение наносов из потока. В
этом случае принимается Sk = Sk-1 (рис. 11, б).
, определенная
по верхней кривой, получается больше, чем в вышерасположенном створе Sk-1, то уменьшение параметра η считается недостаточным для того, чтобы вызвать выпадение наносов из потока. В
этом случае принимается Sk = Sk-1 (рис. 11, б).
б) Если параметр η в рассматриваемом
створе k оказывается больше такового для вышерасположенного створа (k -
1), то есть ηk > ηk-1, то S определяется по нижней кривой - кривой размыва (рис. 11, в). При этом если
оказывается, что определенная по нижней кривой концентрация ![]() получается
меньше, чем в вышерасположенном створе Sk-1, то принимается Sk = Sk-1 (рис. 11,
г).
получается
меньше, чем в вышерасположенном створе Sk-1, то принимается Sk = Sk-1 (рис. 11,
г).
в) Концентрация наносов S в створе гидроузла (k = 0) принимается, как указывалось в п. 6.4, по данным расчета осветления потока водохранилищем. В соответствии с этим, значение S в конце первого расчетного участка (створ k = 1) принимается либо по нижней ветви S = f(η) - при поступлении в нижний бьеф осветленного потока, либо по верхней ветви - при сбросе в нижний бьеф перенасыщенного наносами потока.
6.19. Интенсивность деформации берегов
определяется в зависимости от их геологического строения. При сложении берегов
породами более прочными, чем аллювиальные отложения на дне, обычно принимают
допущение о недеформируемости берегов, то есть считают ![]() .
.
Рис. 11. Схема, поясняющая определение концентрации взвешенных наносов S = f(η) по данным натурных наблюдений
В случае, когда дно и берега сложены песчаным грунтом, интенсивность береговых деформаций может быть определена по приближенной зависимости [9]
![]() (82)
(82)
полученной для условий саморазмыва канала. В случае размыва среднезернистых однородных песчаных грунтов kВ = 0,05, для мелкозернистых заиленных песков значение kВ следует уменьшить до 0,01 - 0,005 [9]. В общем случае коэффициент kВ может быть определен по зависимости
 (83)
(83)
где d - средний диаметр грунта; ![]() - усталостная
прочность на разрыв несвязного грунта, определяемая по формуле (18).
- усталостная
прочность на разрыв несвязного грунта, определяемая по формуле (18).
Учет береговых деформаций ![]() - при
расчетах трансформации русел в нижних бьефах целесообразно осуществлять лишь в
тех случаях, когда они сопоставимы по объему с деформациями дна
- при
расчетах трансформации русел в нижних бьефах целесообразно осуществлять лишь в
тех случаях, когда они сопоставимы по объему с деформациями дна ![]()
6.20. Толщина слоя деформации дна Δzk за время Δt определяется, исходя из зависимости (80), по формуле
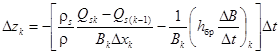 (84)
(84)
(индексы, указывающие номер временной ступени, опущены).
Положительное значение Δzk указывает на то, что на рассматриваемом участке имеет место отложение наносов; отрицательное значение этих величин соответствует размыву дна. Для следующей расчетной временной ступени отметки дна на участке принимаются равными
![]() (85)
(85)
где индекс k означает номер расчетного участка; 0 и 1 - соответственно начало и конец временной ступени.
При выполнении расчетов следует учитывать, что при достижении на том или ином участке в процессе деформации русла кровли неразмываемых пород или отметок, соответствующих образованию слоя отмостки (пп. 6.22 - 6.24), дальнейший размыв русла на этом участке прекращается и, в случае отсутствия отложений, наносы проходят через него транзитом, то есть расход наносов в низовом створе этого участка Qsk принимается равным расходу Qs(k-1), поступившему на этот участок с вышерасположенного: ΔQsk = 0 и Δzk = 0 (здесь индексы, указывающие номер временной ступени, опущены).
6.21. Гидравлические характеристики потока (V и h) при заданном расходе Q на временном шаге Δt определяются построением кривой свободной поверхности на основании решения уравнения Бернулли (77) одним из известных способов. Схема, поясняющая расчет свободной поверхности в деформируемом русле при ступенчатой схематизации, приведена в качестве примера на рис. 12.
6.22. В руслах, образованных разнозернистым несвязным материалом (d95/d5) > 5, в процессе их переформирования может произойти отмостка поверхности дна частицами крупных фракций донных отложений. До тех пор, пока скорости потока V больше значений неразмывающей скорости наиболее крупных частиц Vн.наиб, происходит срыв с поверхности дна частиц всех фракций донных отложений [31, 38, 48]. По мере углубления русла при размыве и уменьшения скоростей потока V до значений, меньших Vн.наиб, срыв наиболее крупных частиц грунта прекращается, и они накапливаются в поверхностном слое, образуя отмостку на новом русле. При дальнейшем углублении русла в состав слоя отмостки вовлекаются и менее крупные частицы. Поверхность русла постепенно покрывается слоем крупных частиц.
Рис. 12. Схема, поясняющая расчет свободной поверхности в деформированном русле
Этот процесс заканчивается, когда вся поверхность будет отмощена панцирем крупных частиц со средневзвешенным диаметром dотм, которому соответствует неразмывающая скорость Vн.отм.
Для образования отмащивающего русло поверхностного слоя крупных частиц со средневзвешенным диаметром dотм поток должен переработать слой грунта толщиной δz, отмыв из него частицы крупностью d < dотм. Слой δz называется слоем накопления отмостки. Вынос мелких фракций при V ≤ Vн.отм происходит лишь путем «отсасывания» их потоком через еще недостаточно сформировавшуюся отмостку.
6.23. Расчет деформации русел, сложенных разнозернистым грунтом (относящихся чаще всего к горным* и предгорным районам), рекомендуется выполнять в следующем порядке [31, 48].
_____________
* Специфические особенности расчета переформирования горных рек см. [33].
1. По кривой гранулометрического состава донных отложений находятся:
средний диаметр грунта d и соответствующая ему ордината pd - доля, составляемая частицами, крупность которых меньше d в общем объеме смеси;
диаметр частиц, определяющих шероховатость русла, d95;
наибольший диаметр частиц dнаиб.
2. Вычисляется коэффициент однородности грунта
Ko = d/d95. (86)
3. По известным характеристикам потока Q, V и h определяются:
неразмывающая скорость Vн для частиц грунта средней крупности d по зависимости (15) или (22) при глубине потока h;
неразмывающая скорость потока Vн.наиб и соответствующая ей начальная глубина hнач, при которой начинается образование самоотмостки русла
Значения Vн.наи6 и hнач находятся путем решения (методом итераций или графически) этого уравнения совместно с зависимостью (22), в которой принимается Vн = Vн.наиб, h = hнач и d = dнаиб.
4. Определяется средний диаметр частиц отмостки dотм и толщина слоя ее накопления δz, связанные между собой зависимостью А.В. Магомедовой - Ц.Е. Мирцхулавы [31, 38, 48]
где δz - толщина переработанного при образовании отмостки слоя грунта (см. п. 6.22) - слоя накопления отмостки.
Нахождение значений dотм и δz осуществляется совместным решением уравнения (88) и зависимостей:
hкон = h + δz, (89)
Q = hконBVн.отм, (90)
где Vн.отм вычисляется по зависимости (22) при h = hкон и d = dотм.
Решение системы уравнений (88) - (90) осуществляется методом итераций, причем в качестве параметра начального приближения может задаваться либо δz, либо dотм*.
_____________
* Из зависимости (88) следует, что при dотм > d95 толщина слоя накопления отмостки δz > 20dотм, а при dотм < d95 этот слой имеет толщину δz ≤ 20dотм.
Полученное в результате решения значение глубины hкон устанавливается в русле, сложенном разнозернистым грунтом с характеристиками d, pd, d95 после размыва его расходом воды Q и самоотмостки крупными частицами со средневзвешенным диаметром dотм; глубина hкон характеризует предельное состояние размыва этого грунта при прохождении расхода Q.
Пример расчета самоотмостки русла представлен в Приложении 3.
6.24. Расчеты русловых деформаций, происходящих с образованием самоотмостки на поверхности размываемого неоднородного по крупности грунта, могут выполняться для двух случаев:
I - последовательный расчет трансформации русла при заданном чередовании гидрографов расчетного периода с определением промежуточных продольных профилей деформации русла, отражающих произошедшие к любому выбранному моменту времени размывы и отложения наносов, а также участки образовавшейся самоотмостки русла, ограничивающей размыв, когда при прохождении расхода воды Q рассчитываемого интервала времени Δt глубина потока h достигает значения hкон, соответствующего Q;
II - расчет на предельный размыв при расчетном расходе воды Q (см. п. 5.2) с определением продольного профиля, формирующегося в результате самоотмостки русла на всей длине исследуемого бьефа и являющегося, как и поверхность неразмываемых пород, границей распространения размывов.
6.25. Результаты расчета трансформации русла в нижнем бьефе должны стать основой для построения кривых Q = f(H) в характерных створах реки, учитывающих переформирование русла на различных этапах эксплуатации гидроузла (например, через 1 год, 5 лет, 10 лет и т.д. после ввода в эксплуатацию).
6.26. Расчет следует вести до полной стабилизации уровней или на период времени, продолжительность которого обусловлена какими-либо дополнительными соображениями (например, сроком ввода в эксплуатацию нижерасположенного гидроузла, подпирающего рассматриваемый бьеф, и т.п.).
6.27. Пример расчета трансформации русла по одному из возможных алгоритмов [8], реализующему решение системы уравнений (71) - (73), дополненной связью (70), а также граничными и начальными условиями по пп. 6.3 - 6.5, приведен в Приложении 4.
Приближенный метод оценки общего размыва
6.28. На предварительных стадиях проектирования, а также при ограниченной исходной информации о морфометрии русла, составе наносов и твердом стоке расчет общего размыва и вызванного им понижения уровней может быть осуществлен по приближенному методу [28]. В основе расчета по этому методу (рис. 13) лежит уравнение баланса наносов в виде
Рис. 13. Схема расчета общего размыва по приближенному методу
где ΔΩ - объем размытого грунта за время Δt; Ps - транспортирующая способность потока за пределами зоны общего размыва, где движение предполагается равномерным, а насыщение потока наносами соответствующим транспортирующей способности. Значение Ps определяется по одной из приведенных в п. 4.10 формул транспортирующей способности.
6.29. Исходное русло нижнего бьефа при расчете по приближенному методу схематизируется в виде призматического канала шириной В, определяемой по имеющемуся картографическому материалу. Уклон дна iо назначается из соображений равенства нормальной глубины потока hо ниже участка размыва средней бытовой глубине при руслоформирующем расходе Qрф (см. п. 5.2).
6.30. Объем размыва, распространяющегося к моменту времени Δt, исчисляемому в приближенном методе с момента пуска гидроузла в эксплуатацию, до створа, удаленного от гидроузла на расстояние х (см. рис. 13), определяется выражением
где ![]() - глубина,
соответствующая предельной неразмывающей скорости потока Vн; х1 - длина участка местного размыва, принимаемая при отсутствии
точных данных равной 200 - 500 м; ΔН - понижение уровня воды в
створе гидроузла.
- глубина,
соответствующая предельной неразмывающей скорости потока Vн; х1 - длина участка местного размыва, принимаемая при отсутствии
точных данных равной 200 - 500 м; ΔН - понижение уровня воды в
створе гидроузла.
При наличии данных о выходе размыва на скальные или трудноразмываемые породы, а также в случае возможности образования самоотмостки, в выражение (91) должны быть внесены соответствующие поправки, учитывающие отличие тела размыва от треугольника.
6.31. Рекомендуется следующий порядок расчета по приближенному методу:
1) определяются параметры расчетного русла (B, io, ho), руслоформирующий расход Qрф, транспортирующая способность Ps и продолжительность расчетного года;
2) строится профиль размытого русла (см. рис. 13) с распространением зоны размыва на длину х;
3) определяется положение свободной поверхности в размытом русле и значение ΔН;
4) по зависимости (92) определяется ΔΩ и затем из уравнения (91) - Δt;
5) назначается большее значение величины х, определяется соответствующее ему ΔН и т.д.
6.32. Примеры расчета общего размыва по приближенному методу для условий однородного и разнородного по крупности грунта приведены в Приложении 5.
7. РАСЧЕТ ПОЛЕЙ
ДЕФОРМАЦИИ РУСЛА
(Двухмерная плановая задача)
7.1. Расчет трансформации русел в нижних бьефах гидроузлов охватывает, как правило, достаточно протяженные участки реки (см. п. 2.8), и в тех случаях, когда основной целью расчетов является составление прогноза изменений уровней воды в нижнем бьефе, происходящих вследствие русловых переформирований, оправданным и целесообразным является применение одномерной модели, дающей достаточное представление о средних по сечению речного русла деформациях дна. В тех случаях, когда по каким-либо соображениям необходимо получить представление о распределении деформаций русла в том или ином сечении, расчет следует проводить с помощью двухмерной плановой модели руслового потока, учитывающей распределение скоростей по его ширине, многорукавность и криволинейность русла, очертание речной долины в плане. Необходимость в выполнении таких расчетов может возникнуть тогда, когда нужно оценить влияние русловых переформирований на хозяйственные и/или инженерные объекты, надежная и безопасная эксплуатация которых связана с возможными изменениями речного дна (мостовые переходы, водозаборные сооружения, воднотранспортные сооружения, переходы трубопроводов различного назначения, защитные дамбы и т.п.) либо тогда, когда нужно оценить влияние сооружений на русловой процесс. В большинстве случаев для решения такого рода задач проведение расчетов на двухмерной модели является необходимым не на всей длине изучаемого бьефа. Достаточно выделить участок ограниченной протяженности и задать для него граничные условия в верховом и низовом граничных створах, например, по результатам решения одномерной задачи. Решение двухмерной плановой задачи явится, таким образом, детализацией решения одномерной задачи в части распределения деформаций речного русла по ширине потока.
7.2. В основе расчета плановой задачи русловых деформаций лежат уравнения мелкой воды Сен-Венана [26, 57], применимые для расчетов водотоков, плановые размеры которых существенно превышают глубину потока:
где qx = hux, qy = huy - удельные
расходы воды в направлении осей координат х и у;
их и иу - проекции осредненной по глубине скорости потока на оси х и у;
h - глубина потока; Н =h
+ z - отметка свободной поверхности воды; z - отметка поверхности дна; Ωc = 2ωsinφ - параметр Кориолиса; ω - угловая
скорость вращения Земли; φ - географическая широта местности; τдx и τду - проекции силы трения о дно на оси х и у, определяемые зависимостями 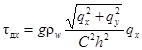 и
и 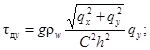 С - коэффициент Шези,
определяемый по зависимости Манинга
С - коэффициент Шези,
определяемый по зависимости Манинга ![]() τxx, τxy, τyx, τyy - осредненные по глубине касательные
напряжения, которые могут быть представлены [57] в виде
τxx, τxy, τyx, τyy - осредненные по глубине касательные
напряжения, которые могут быть представлены [57] в виде
где индексы i, j соответствуют х, y.
В правой части уравнения (93) членом q учитывается интенсивность источника (стока) воды в точке с координатами (х, у), который не привносит в поток дополнительного импульса. В случае, когда источники массы дают дополнительный приток импульса в поток, он должен быть учтен в уравнениях (94) и (95).
Входящий в зависимость (96) коэффициент турбулентной
вязкости vt может
быть определен, например, на основе модели Прандтля vt = ku*h, ![]() где k = 0,4 - постоянная Кармана.
где k = 0,4 - постоянная Кармана.
7.3. Расчет перемещения потоком наносов целесообразно производить раздельно для взвешенных и влекомых наносов. При преобладающей роли в процессе трансформации русла взвешенных наносов уравнение их транспорта целесообразно использовать в следующем виде [15, 59]
![]() (97)
(97)
где ![]() - осредненная по глубине концентрация
наносов;
- осредненная по глубине концентрация
наносов; ![]() - коэффициент связи придонной и средней по глубине концентрации
наносов; w - гидравлическая крупность частиц наносов; sm - концентрация
наносов, соответствующая транспортирующей способности потока; qs - интенсивность
источника массы твердых частиц, обусловленная источником жидкости q (см. (93)); D - суммарный коэффициент диффузии взвешенных наносов в горизонтальной
плоскости (с учетом дисперсии). По направлениям координатных осей коэффициенты
диффузии принимаются одинаковыми Dxx = Dyy = D = ku*L, где L - масштаб вихрей в плане, пропорциональный средней ширине потока (L ~ В).
- коэффициент связи придонной и средней по глубине концентрации
наносов; w - гидравлическая крупность частиц наносов; sm - концентрация
наносов, соответствующая транспортирующей способности потока; qs - интенсивность
источника массы твердых частиц, обусловленная источником жидкости q (см. (93)); D - суммарный коэффициент диффузии взвешенных наносов в горизонтальной
плоскости (с учетом дисперсии). По направлениям координатных осей коэффициенты
диффузии принимаются одинаковыми Dxx = Dyy = D = ku*L, где L - масштаб вихрей в плане, пропорциональный средней ширине потока (L ~ В).
Изменение отметок дна определяется соотношением
![]() (98)
(98)
где δ - пористость грунта (см. п. 3.6).
Коэффициент ![]() перехода от средней по глубине
концентрации взвешенных наносов к придонной концентрации может быть определен [60] по зависимости
перехода от средней по глубине
концентрации взвешенных наносов к придонной концентрации может быть определен [60] по зависимости
 (99)
(99)
Для расчетов концентрации sm могут использоваться различные формулы, применимые для определения транспортирующей способности потока, переносящего наносы во взвешенном состоянии, то есть при u*/w > 1,7 (см. условие (29)). К числу таких формул могут быть отнесены формула К.И. Российского и И.А. Кузьмина (32), формулы А.В. Караушева (43), Р.А. Бэгнольда (46), приведенные путем деления на расход Q к размерности концентрации. С некоторой осторожностью может использоваться формула В.И. Гончарова (44), также приведенная к размерности концентрации. Как и в случае одномерной задачи, критерием предпочтительности применения той или иной из названных зависимостей является удовлетворительное совпадение ее с результатами имеющихся натурных наблюдений.
7.4. При преобладающей роли в процессе русловых переформирований влекомых наносов изменение отметок дна может быть определено из уравнения русловых деформаций (73), представленного в виде
![]() (100)
(100)
где qsx и qsy - проекции
удельных расходов наносов на оси х и у, ![]() ,
, ![]() Значения
Значения ![]() определяются по формуле транспортирующей способности потока,
переносящего наносы путем сальтации и влечения по дну, то есть по формуле
справедливой при u*/w < 1,7 .
Наиболее удобными для применения в таких расчетах являются зависимости И.И. Леви (37) и (38),
приведенные путем деления на расход Q к условной размерности концентрации. Полученные в результате
вычисления значения интенсивности деформации при размыве
определяются по формуле транспортирующей способности потока,
переносящего наносы путем сальтации и влечения по дну, то есть по формуле
справедливой при u*/w < 1,7 .
Наиболее удобными для применения в таких расчетах являются зависимости И.И. Леви (37) и (38),
приведенные путем деления на расход Q к условной размерности концентрации. Полученные в результате
вычисления значения интенсивности деформации при размыве ![]() не должны превышать
значений размывающей способности потока Рp, определяемой
по зависимости (49). В случае,
когда
не должны превышать
значений размывающей способности потока Рp, определяемой
по зависимости (49). В случае,
когда ![]() ,
значение
,
значение ![]() должно быть принято таким, чтобы соблюдалось точное равенство
должно быть принято таким, чтобы соблюдалось точное равенство ![]()
Учет образования самоотмостки при размыве разнозернистого грунта должен производиться по
зависимостям п. 6.23 с заменой в
них полного расхода воды Q на удельный
расход q путем отнесения его к единице ширины по нормали к вектору
средней по глубине скорости потока ![]()
7.5. В качестве начальных условий должны быть заданы координаты рельефа в пределах расчетной области, включая затопляемую часть долины и острова, значения скоростей, глубин потока в характерных точках. Кроме того, должны быть заданы характеристики шероховатости русла и донных отложений.
7.6. В качестве граничных условий должны быть заданы на всем протяжении расчетной области «твердые» границы речного потока: координаты дна и берегов, включая острова, во всем диапазоне возможного изменения уровней воды.
Граничными условиями в верховом (входном) створе являются данные о втекающем в расчетную область жидком и твердом расходах и об отметках свободной поверхности, полученные в результате решения одномерной задачи. Распределение жидких расходов по ширине створа может быть принято в первом приближении пропорционально глубине потока, а направление скоростей течения - ориентированным вдоль берегов или динамической оси потока в зависимости от положения в поперечном сечении.
В низовом граничном створе должна быть задана закономерность изменения отметок свободной поверхности по результатам решения одномерной задачи. Если в процессе расчетов двухмерной модели будет отмечаться несовпадение заданных и рассчитанных отметок поверхности, необходимо произвести уточнение характеристик шероховатости с тем, чтобы достигнуть приемлемого совпадения уровней.
7.7. В связи с условностью предположений о распределении характеристик руслового потока по ширине входного створа, а также в связи с тем, что очертания русла ниже низового створа могут влиять на характеристики течения в расчетной области, местоположение граничных створов следует назначать выше и ниже истинных границ этой области на расстоянии от них не менее 3-х ширин потока.
7.8. Примеры возможных алгоритмов решения плановой задачи русловых деформаций и их реализации для конкретных условий приведены в [21, 58].
СПИСОК ЛИТЕРАТУРЫ
1. Алексеевский Н.И. Формирование и движение речных наносов. М.: Изд-во МГУ. 1998.
2. Беркович К.М., Чалов Р.С., Чернов А.В. Экологическое русловедение. М.: ГЕОС. 2000.
4. Векслер А.Б. О преобразовании уравнений пространственного потока применительно к условиям его одноразмерной модели // Сборник докладов по гидротехнике / ВНИИГ им. Б.Е. Веденеева. 1970. Вып. 11. С. 194 - 207.
10. Гончаров В.Н. Основы динамики русловых потоков. Л.: Гидрометеоиздат. 1954.
11. Гончаров В.Н. Динамика русловых потоков. Л.: Гидрометеоиздат. 1962.
12. Гришанин К.В. Динамика русловых потоков. Л.: Гидрометеоиздат. 1979.
13. Гришанин К.В. Основы динамики русловых потоков. М.: Транспорт. 1990.
18. Караушев А.В. Проблемы динамики естественных водных потоков. Л.: Гидрометеоиздат. 1960.
19. Караушев А.В. Речная гидравлика. Л.: Гидрометеоиздат. 1969.
28. Леви И.И. Динамика русловых потоков. М.-Л.: Госэнергоиздат. 1957.
29. Леви И.И. Инженерная гидрология. М.: Высшая школа. 1968.
31. Магомедова А.В. Эрозионные процессы в руслах рек и каналов. М.: Изд-во ВЗПИ. 1990.
34. Мирцхулава Ц.Е. Размыв русел и методика оценки их устойчивости. М.: Колос. 1967.
37. Мирцхулава Ц.Е. Надежность гидромелиоративных сооружений. М.: Колос. 1974.
38. Мирцхулава Ц.Е. Основы физики и механики эрозии русел. Л.: Гидрометеоиздат. 1988.
42. Романовский В.В. Исследования начальной скорости влечения частиц наносов // Труды ГТИ. Л.: Гидрометеоиздат. 1974. Вып. 210 С. 130 - 150.
44. Российский К.И. Расчет движения речных наносов // Труды Гидропроекта. 1973. № 30. С. 14 - 36.
47. Российский К.И., Дебольский В.К. Речные наносы. М.: Наука. 1980.
54. Чертоусов М.Д. Гидравлика. Специальный курс. М.-Л.: Госэнергоиздат. 1957.
55. Чугаев Р.Р. Гидравлика (техническая механика жидкости). Л.: Энергия. 1975.
60. Raudkivi A.J. Loose Boundary Hydraulics. A.A. Balkema Publishers. Rotterdam. 1998.
ПРИЛОЖЕНИЕ 1
СХЕМАТИЗАЦИЯ РУСЛА
Выполнить схематизацию русла в нижнем бьефе гидроузла
Гидроузел возведен на реке, план и продольный профиль которой на примыкающем к гидроузлу участке представлен на рис. П1.1.
Сечение русла принято прямоугольным с постоянной в пределах расчетного участка шириной, равной средней ширине в бровках (по данным изысканий). При разбивке на участки в основу положен принцип однообразия плановых очертаний русла и его рельефа. Длина расчетного бьефа ограничена участком протяженностью 75,5 км, ниже которого влияние гидроузла предполагается незначительным. Участки, примыкающие к гидроузлу, приняты более короткими, чем удаленные от него. Разбивка расчетного бьефа на участки, их принятые длина и ширина показаны на рис. П1.1.
Рис. П1.1. Схематизация русла: план (а) и продольный профиль (б):
![]() - среднемноголетняя свободная поверхность
в бытовом состоянии;
- среднемноголетняя свободная поверхность
в бытовом состоянии; ![]() - схематизированное
среднемноголетнее дно в бытовом состоянии;
- схематизированное
среднемноголетнее дно в бытовом состоянии; ![]() - свободная поверхность и дно по результатам расчета за 20
лет
- свободная поверхность и дно по результатам расчета за 20
лет
Для створов, в которых имеются кривые связи (рис. П1.2), строятся (по п. 5.14) графические зависимости (рис. П1.3), аппроксимируя которые прямыми, можно определить по пересечению их с осью у значения - искомые условные отметки дна z в рассматриваемых створах. Полученные таким образом отметки (табл. П1.1) служат основой для построения линии схематизированного дна, по которой строится продольный профиль расчетного русла.
Рис. П1.2. Зависимости Q = f(H) в створах нижнего бьефа гидроузла
0 - 8 - номера расчетных створов
Рис. П1.3. Аппроксимация кривых Q = f(H) прямыми ![]() в расчетных створах:
в расчетных створах:
числа на кривых указывают расстояние от створа ГЭС в км и
номер расчетного створа; ![]() кривые расходов в различных створах;
кривые расходов в различных створах; ![]() линейная
аппроксимация
линейная
аппроксимация
Таблица П1.1
Отметки дна z = у0 в расчетных и промежуточных створах бьефа
|
Расстояние от створа гидроузла, км |
Отметка дна z, м |
|
|
0 (створ плотины) |
0 |
12,05 |
|
1 |
3,1 |
11,85 |
|
2 |
8,3 |
10,95 |
|
3 |
15,5 |
10,50 |
|
4 |
21,3 |
10,00 |
|
5 |
26,1 |
9,80 |
|
6 |
41,4 |
9,00 |
|
7 |
61,1 |
7,05 |
|
8 |
75,5 |
5,35 |
ПРИЛОЖЕНИЕ 2
ОПРЕДЕЛЕНИЕ РАСЧЕТНЫХ ХАРАКТЕРИСТИК ВЗВЕШЕННЫХ НАНОСОВ ПО ДАННЫМ НАТУРНЫХ НАБЛЮДЕНИЙ
Определить долю руслоформирующих фракций в общем количестве наносов.
Имеются следующие натурные данные:
а) фракции, присутствующие во взвешенных наносах и донных отложениях, имеют размер: 0,5 - 0,25 мм, 0,25 - 0,10 мм и 0,10 - 0,05 мм, причем в составе донных отложений эти фракции составляют в среднем 77 %;
б) эти же фракции во взвешенных наносах составляют в 4-х точках вертикали, удаленных от поверхности на 0,2; 0,6; 0,8 и 1,0 глубины, соответственно 36; 45; 40,3 и 77 %.
Следовательно, среднее содержание руслоформирующих фракций kрф во взвешенных наносах по формуле (34) равно
(36 + 45 + 40,3 + 77)/(100 ∙ 4) = 0,5.
Данные измерений мутности на водпостах, расположенных на изучаемом участке реки, приведенные в «Гидрологических ежегодниках» и полученные в результате изысканий под проект гидроузла, умножаются на kрф = 0,5 и используются при построении зависимости S = f(η).
Для построения вспомогательного графика ε = f(V3/h) с целью определения w вместо S и η вводятся новые переменные ε = ρsS и V3/h (п. 4.4).
Обработанные в координатах ε и V3/h эти данные образовали единое поле точек (рис. П2.1) с верхней огибающей, описываемой уравнением
εв = 667V3/h, т/м3.
На основании формулы (32) для этой огибающей получено
![]()
откуда следует w = 0,0363 м/с, что при температуре воды в период прохождения паводка ≈5 - 10 °С (табл. 5) соответствует среднему диаметру грунта d = 0,36 мм (при ρs = 2650 кг/м3).
Соответственно для нижней огибающей принимается ε =135V3/h (г/м3) при V3/h < 0,25. При V3/h > 0,25 в соответствии с расположением данных измерений зависимость εн = f(V3/h) принята отличной от линейной.
Принимая значение w одинаковым для верхней и нижней огибающих поля точек, можно построить рис. П2.2 в координатах S и η, и по нему найти значения а и α для ветви размыва (нижняя огибающая).
Рис. П2.1. Зависимость εрф = f(V3/h)
Рис. П2.2. Зависимость S = f(η)
Оба графика (см. рис. П2.1 и П2.2) являются равноценными. Предпочтительно использование безразмерной связи S = f(η) и получаемых из нее параметров а, α, b, β.
Нижняя кривая - S = а(η - ηн)α

![]()
Верхняя кривая - S = bηβ
![]() β = 1,0.
β = 1,0.
ПРИЛОЖЕНИЕ 3
РАСЧЕТ ОБРАЗОВАНИЯ САМООТМОСТКИ В РУСЛЕ, СЛОЖЕННОМ РАЗНОЗЕРНИСТЫМ ГРУНТОМ
Дать прогноз образования отмостки на участке нижнего бьефа гидроузла.
Гидроузел возведен на реке, дно которой сложено разнозернистым несвязным (гравийно-галечниковым) грунтом, гранулометрия которого представлена на рис. П3.1 и характеризуется следующими данными: средний диаметр d = 49 мм, pd = 61 %, d95 = 150 мм, dнаиб = 200 мм, ρs = 2650 кг/м3.
Рис. П3.1. Кривая гранулометрического состава наносов
Коэффициент однородности грунта по формуле (86)
![]()
то есть грунт неоднороден и при его размыве должна образовываться отмостка.
Характеристики условно равномерного потока на рассматриваемом участке: Q0,01% = 4380 м3/с; В = 190 м; h = 4,95 м; V = 4,66 м/с; mм = 1.
По (22) определяется значение неразмывающей скорости для dнаиб

В первом приближении
принимается ![]() и тогда
и тогда
![]()
соответствующая такой
скорости по (87) глубина ![]()
Так как полученное значение ![]() методом последовательных
приближений находятся
методом последовательных
приближений находятся
![]()
и
![]()
то есть скорость потока V > Vн.наиб, и в соответствии с п. 6.23 (3) в русле будет происходить размыв всех фракций до достижения потоком глубины hнач = 6,8 м, после чего начнется образование отмостки.
Для определения характеристик отмостки используется система уравнений (88) - (90), которая с учетом исходных условий примера представляется в следующем виде:

Q = hконBVн.отм,
![]()
hкон = hнач + δz.
Полученная система может быть решена способом последовательных приближений или графически. Для реализации графического способа задается несколько значений δz, после чего по уравнениям системы находятся соответствующие им значения dотм, hкон и Q (табл. П3.1).
Таблица П3.1
Расчет отмостки
|
δz, м |
0,5 |
0,75 |
1,00 |
1,25 |
1,50 |
|
d + 0,374δz, м |
0,236 |
0,330 |
0,423 |
0,516 |
0,610 |
|
d95 + 0,34δz, м |
0,320 |
0,405 |
0,490 |
0,575 |
0,660 |
|
dотм, м |
0,111 |
0,122 |
0,129 |
0,134 |
0,139 |
|
hкон, м |
7,30 |
7,55 |
7,80 |
8,05 |
8,30 |
|
Vн.отм, м/с |
2,55 |
2,69 |
2,78 |
2,85 |
2,91 |
|
Q, м3/с |
3573 |
3859 |
4120 |
4359 |
4589 |
Построив по данным табл. П3.1 графики hкон = f(Q), dотм = f(Q) и Vн.отм = f(Q), можно найти по ним значения hкон = 8,07 м, dотм = 0,134 м и Vн.отм = 2,86 м/с, которые соответствуют заданному расчетному расходу Q0,01% = 4380 м3/с (рис. П3.2).
Рис. П3.2. Графики для нахождения параметров самоотмостки русла
ПРИЛОЖЕНИЕ 4
РАСЧЕТ ТРАНСФОРМАЦИИ РУСЛА НИЖНЕГО БЬЕФА ГИДРОУЗЛА
Выполнить расчет трансформации русла реки в нижнем бьефе гидроузла (рис. П1.1) для участка, ограниченного створом x = 30,3 км.
Русло нижнего бьефа схематизируется в предположении линейного изменения ширин и отметок дна в пределах каждого расчетного участка. Живые сечения приняты прямоугольными. Параметры створов приведены в табл. П4.1.
Таблица П4.1
Параметры створов
|
Продольная координата x, м |
Ширина В, м |
Начальная отметка дна z, м |
Отметка коренных пород zпред, м |
|
|
1 |
100 |
850 |
91,65 |
89,80 |
|
2 |
1100 |
1200 |
93,03 |
89,60 |
|
3 |
2100 |
950 |
92,15 |
89,50 |
|
4 |
2600 |
950 |
91,50 |
89,35 |
|
5 |
3100 |
800 |
91,85 |
89,20 |
|
6 |
5000 |
650 |
90,80 |
89,60 |
|
7 |
6600 |
950 |
92,50 |
89,00 |
|
8 |
7000 |
900 |
91,65 |
88,30 |
|
9 |
8300 |
750 |
90,50 |
88,70 |
|
10 |
9900 |
800 |
90,85 |
88,45 |
|
11 |
10400 |
850 |
92,00 |
88,25 |
|
12 |
11300 |
750 |
90,10 |
88,10 |
|
13 |
13000 |
950 |
90,80 |
88,25 |
|
14 |
13800 |
650 |
89,15 |
87,90 |
|
15 |
15500 |
900 |
90,50 |
87,50 |
|
16 |
16300 |
800 |
89,55 |
88,35 |
|
17 |
17400 |
1050 |
91,50 |
88,40 |
|
18 |
18200 |
1000 |
90,60 |
88,45 |
|
19 |
18500 |
1200 |
91,50 |
88,25 |
|
20 |
19600 |
1050 |
90,85 |
88,10 |
|
21 |
21300 |
900 |
90,25 |
87,45 |
|
22 |
22400 |
750 |
89,00 |
87,30 |
|
23 |
24400 |
650 |
88,50 |
87,50 |
|
24 |
26100 |
1000 |
90,25 |
88,10 |
|
25 |
27600 |
1100 |
90,50 |
87,30 |
|
26 |
30300 |
900 |
88,75 |
87,80 |
Каждый из 25 основных участков, ограниченных створами с характеристиками, приведенными в табл. П4.1, разбит на подучастки (от 2 до 26), дополнительное разбиение которых в процессе расчета выполняется автоматически с коэффициентом деления подучастка наименьшей площади, равным 2.
Использованный алгоритм расчета позволяет учесть следующие факторы: постепенность насыщения потока наносами, самоотмостку русла крупными фракциями грунта, местные сопротивления за счет изменения ширины русла вдоль потока, сосредоточенные притоки, карьерные разработки русла, размываемость берегов.
Расчетный гидрограф схематизирован в виде расходов воды на 200-х временных интервалах, охватывающих период продолжительностью 20 лет (условно с 1957 по 1976 гг.), и представлен в виде таблицы, фрагменты которой (начало и конец) приведены в табл. П4.2. В процессе расчета каждый интервал разбивается на шаги таким образом, чтобы изменение глубины h потока за один шаг нигде не превосходило заданного значения. В представленных примерах это значение принято равным 0,001h.
Максимальный за период, охваченный расчетом, расход воды составляет 9760 м3/с и приходится на 14-ю ступень - пик паводка второго (1958) года.
Расчет трансформации русла предваряется нахождением коэффициентов шероховатости русла на участках между опорными створами, в которых заданы кривые связи расходов и уровней воды в начальный момент времени (рис. П4.1). Найденные таким образом и принятые для последующих расчетах значения коэффициентов шероховатости приведены в табл. П4.3.
Начальная свободная поверхность задана в виде таблицы, в которой для каждого из 26 основных створов указаны отметки уровня воды при расходах 500, 1000, 2000, 3000, 5000, 7500, 10000, 15000 м3/с.
Основные расчетные параметры грунта на участках рассчитываемого бьефа приняты на основе обработки данных натуры и приводятся в табл. П4.4.
Приток находится в створе 18. Заданы таблицы расходов притока и таблицы влияния притока на уровни воды в створах 15 - 18 основного русла, а также плотность ps = 2,65 т/м3 и средняя крупность d = 1,5 мм наносов притока.
Расход наносов в начальном створе (створе гидроузла) принимается равным нулю, т.е. поток, поступающий в нижний бьеф, считается полностью осветленным. Транспортирующая способность потока в остальных створах определяется по формуле И.И. Леви (37). Для других условий задачи алгоритм предусматривает использование других зависимостей, в том числе и зависимостей вида (31), если имеются данные натурных наблюдений за мутностью потока (см. например, рис. П2.2).
Таблица П4.2
Расчетный гидрограф
|
Номер ступени |
Расход Q, м3/с |
Длительность, сутки |
|
|
1957 |
1 |
1000 |
100 |
|
2 |
3200 |
10 |
|
|
3 |
6500 |
5 |
|
|
4 |
7510 |
3 |
|
|
5 |
6950 |
7 |
|
|
6 |
5500 |
20 |
|
|
7 |
3900 |
20 |
|
|
8 |
1900 |
26 |
|
|
9 |
1000 |
124 |
|
|
10 |
1000 |
50 |
|
|
1958 |
11 |
1000 |
100 |
|
12 |
3600 |
10 |
|
|
13 |
8200 |
6 |
|
|
14 |
9760 |
1 |
|
|
15 |
9200 |
8 |
|
|
16 |
8000 |
17 |
|
|
17 |
6000 |
2 |
|
|
18 |
2630 |
24 |
|
|
19 |
1000 |
97 |
|
|
20 |
1000 |
100 |
|
|
........ |
........ |
........ |
........ |
|
........ |
........ |
........ |
........ |
|
1976 |
191 |
1000 |
100 |
|
192 |
1600 |
10 |
|
|
193 |
2600 |
7 |
|
|
194 |
3600 |
1 |
|
|
195 |
3200 |
7 |
|
|
196 |
2500 |
15 |
|
|
197 |
2000 |
2 |
|
|
198 |
1400 |
26 |
|
|
199 |
1000 |
147 |
|
|
200 |
1000 |
50 |
Расчет выполнен для двух случаев.
Пример 1. Грунт ложа реки разнозернистый; учитывается самоотмостка русла крупными фракциями грунта; карьерных разработок русла нет;
Пример 2. Грунт ложа реки однородный, характеризующийся в пределах каждого участка средней крупностью d, указанной в табл. П4.4 (самоотмостка отсутствует); производятся карьерные разработки русла.
Таблица П4.3
Коэффициенты пш (по Маннингу)
|
Расходы воды, м3/с |
||||||||
|
500 |
1000 |
2000 |
3000 |
5000 |
7500 |
10000 |
15000 |
|
|
1 - 5 |
0,0295 |
0,0416 |
0,0426 |
0,0461 |
0,0387 |
0,0345 |
0,0329 |
0,0289 |
|
5 - 9 |
0,0430 |
0,0398 |
0,0411 |
0,0363 |
0,0307 |
0,0254 |
0,0216 |
0,0191 |
|
9 - 15 |
0,0507 |
0,0433 |
0,0399 |
0,0362 |
0,0327 |
0,0273 |
0,0280 |
0,0204 |
|
15 - 21 |
0,0280 |
0,0297 |
0,0327 |
0,0346 |
0,0317 |
0,0312 |
0,0283 |
0,0271 |
|
21 - 24 |
0,0595 |
0,0430 |
0,0331 |
0,0305 |
0,0297 |
0,0285 |
0,0246 |
0,0247 |
|
24 - 26 |
0,0255 |
0,0286 |
0,0281 |
0,0308 |
0,0296 |
0,0218 |
0,0158 |
0,0144 |
Таблица П4.4
Значения основных расчетных параметров грунта на участках между створами
|
ρгр, т/м3 |
ρs, т/м3 |
Параметры в формуле (15) |
d, м |
d95, м |
pd |
||
|
mм |
Kс |
||||||
|
1 - 6 |
1,5 |
2,65 |
1,0 |
2,0 |
0,00048 |
0,0015 |
0,72 |
|
6 - 16 |
1,5 |
2,65 |
1,0 |
2,0 |
0,00045 |
0,0013 |
0,75 |
|
16 - 24 |
1,5 |
2,65 |
1,0 |
2,0 |
0,00030 |
0,0010 |
0,70 |
|
24 - 26 |
1,5 |
2,65 |
1,0 |
2,0 |
0,00035 |
0,0012 |
0,73 |
Интенсивность карьерных разработок задана в виде таблицы, в которой указаны объемы грунта, извлекаемого в заданные временные интервалы на заданных участках русла. Фрагменты такой таблицы представлены в табл. П4.5.
При выполнении расчетов учитывались местные гидравлические сопротивления русла и принимались следующие значения постоянных величин для условий решаемых задач:
корректив Кориолиса α = 1,0;
кинематический коэффициент вязкости воды v = 0,00000131 м2/с;
плотность воды ρw = 1,0 т/м3;
показатель степени в формуле (30) m = 1;
Результаты расчетов для примеров 1 и 2 представлены на рис. П4.2 - П4.6.
Таблица П4.5
Объемы карьерных разработок на участках W, тыс. м3
|
Номера участков |
|||||||||
|
2 |
3 |
7 |
8 |
9 |
10 |
16 |
20 |
24 |
|
|
39 |
184,04 |
91,88 |
17,40 |
56,65 |
297,74 |
0,00 |
148,10 |
0,00 |
74,04 |
|
48 |
32,47 |
16,21 |
3,08 |
10,01 |
52,66 |
0,00 |
26,20 |
0,00 |
13,10 |
|
49 |
155,37 |
77,57 |
14,68 |
47,78 |
251,16 |
0,00 |
124,92 |
0,00 |
62,46 |
|
....... |
....... |
....... |
....... |
....... |
....... |
....... |
....... |
....... |
....... |
|
....... |
....... |
....... |
....... |
....... |
....... |
....... |
....... |
....... |
....... |
|
157 |
1,83 |
0,91 |
0,64 |
2,07 |
3,54 |
0,00 |
5,43 |
37,71 |
2,72 |
|
158 |
23,77 |
11,89 |
8,29 |
26,99 |
46,06 |
0,00 |
70,57 |
490,29 |
35,29 |
|
159 |
134,40 |
67,20 |
46,88 |
152,62 |
260,40 |
0,00 |
399,00 |
2772,00 |
199,50 |
|
168 |
3,47 |
1,73 |
7,13 |
23,20 |
81,47 |
0,00 |
60,67 |
121,33 |
82,33 |
|
....... |
....... |
....... |
....... |
....... |
....... |
....... |
....... |
....... |
....... |
|
....... |
....... |
....... |
....... |
....... |
....... |
....... |
....... |
....... |
....... |
|
197 |
0,00 |
0,00 |
0,95 |
3,11 |
5,71 |
4,57 |
8,12 |
0,00 |
4,05 |
|
198 |
0,00 |
0,00 |
12,39 |
40,35 |
74,29 |
59,43 |
105,49 |
0,00 |
52,74 |
|
199 |
0,00 |
0,00 |
70,08 |
228,12 |
420,00 |
336,00 |
596,40 |
0,00 |
298,20 |
Рис. П4.1. Кривые связи расходов и уровней воды в опорных створах для примеров 1 и 2 в начальный момент:


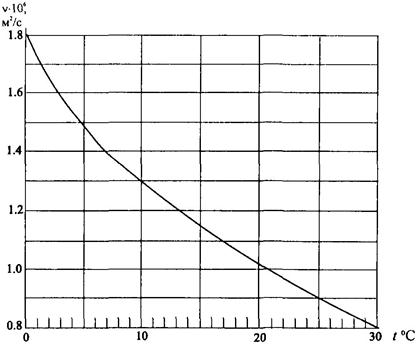

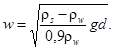
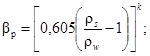
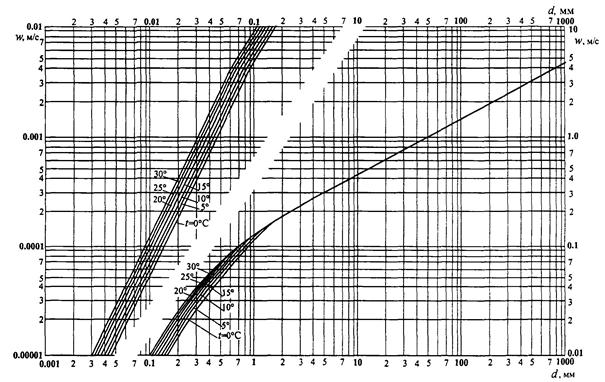
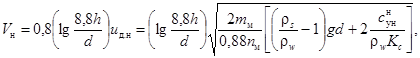





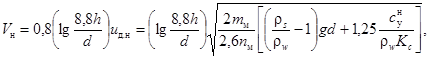
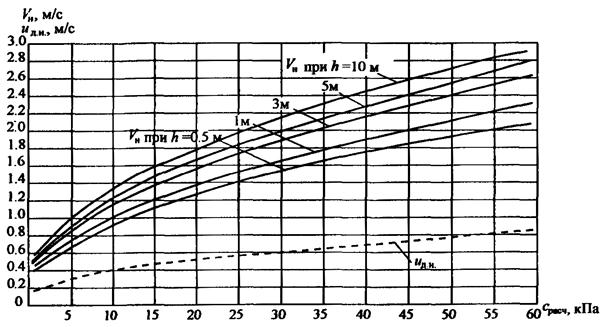



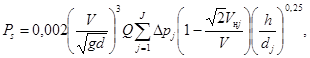

 (44)
(44)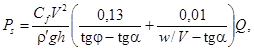
 (49)
(49)
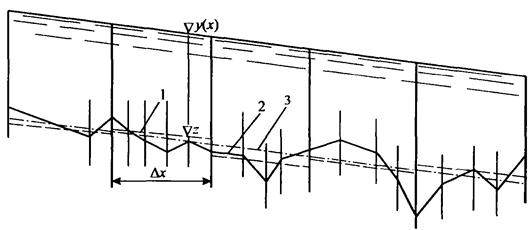
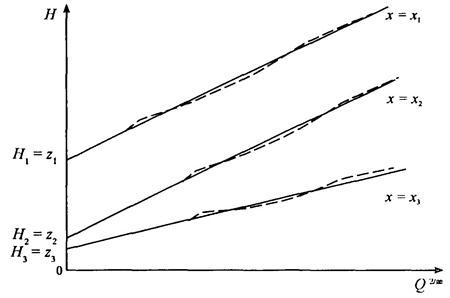

 (63)
(63)
 (66)
(66) (70)
(70)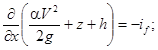 (71)
(71)