ФЕДЕРАЛЬНОЕ
АГЕНТСТВО
ПО ТЕХНИЧЕСКОМУ РЕГУЛИРОВАНИЮ И МЕТРОЛОГИИ
|
|
НАЦИОНАЛЬНЫЙ |
ГОСТ Р МЭК |
Надежность в технике
КРИТЕРИИ
ПРОВЕРКИ ПОСТОЯНСТВА
ИНТЕНСИВНОСТИ ОТКАЗОВ И ПАРАМЕТРА
ПОТОКА ОТКАЗОВ
IEC
60605-6:2007
Equipment reliability testing - Part 6: Tests for the validity and estimation
of the
constant failure rate and constant failure intensity
(IDT)
|
|
Москва Стандартинформ 2008 |
Предисловие
Цели и принципы стандартизации в Российской Федерации установлены Федеральным законом от 27 декабря 2002 г. № 184-ФЗ «О техническом регулировании», а правила применения национальных стандартов Российской Федерации - ГОСТ Р 1.0-2004 «Стандартизация в Российской Федерации. Основные положения»
Сведения о стандарте
1 ПОДГОТОВЛЕН Открытым акционерным обществом «Научно-исследовательский центр контроля и диагностики технических систем» (ОАО «НИЦ КД») на основе собственного аутентичного перевода стандарта, указанного в пункте 4
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 119 «Надежность в технике»
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 27 декабря 2007 г. № 579-ст
4 Настоящий стандарт идентичен международному стандарту МЭК 60605-6:2007 «Испытания оборудования на надежность. Часть 6. Критерии проверки постоянства интенсивности отказов и параметра потока отказов и методы их оценки» (IEC 60605-6:2007 «Equipment reliability testing - Part 6: Tests for the validity and estimation of the constant failure rate and constant failure intensity»).
Наименование настоящего стандарта изменено относительно наименования указанного международного стандарта для приведения в соответствие с ГОСТ Р 1.5-2004 (подраздел 3.5).
При применении настоящего стандарта рекомендуется использовать вместо ссылочных международных стандартов соответствующие им национальные стандарты, сведения о которых приведены в дополнительном приложении D
5 ВВЕДЕН ВПЕРВЫЕ
Информация об изменениях к настоящему стандарту публикуется в ежегодно издаваемом информационном указателе «Национальные стандарты», а текст изменений и поправок - в ежемесячно издаваемых информационных указателях «Национальные стандарты». В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ежемесячно издаваемом информационном указателе «Национальные стандарты». Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет
СОДЕРЖАНИЕ
Введение
В настоящем стандарте приведены числовые и графические методы проверки постоянства интенсивности отказов и параметра потока отказов. Графические методы позволяют идентифицировать непостоянство интенсивности отказов и параметра потока отказов и выявить ранние отказы. Методы подходят для анализа результатов испытаний и данных эксплуатации.
ГОСТ Р МЭК 60605-6-2007
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
|
Надежность в технике КРИТЕРИИ
ПРОВЕРКИ ПОСТОЯНСТВА ИНТЕНСИВНОСТИ ОТКАЗОВ И ПАРАМЕТРА ПОТОКА Reliability in techniques. Tests for the validity of the constant failure rate and failure intensity |
Дата введения - 2008-09-01
1 Область применения
Настоящий стандарт устанавливает методы проверки предположений о постоянстве интенсивности отказов и параметра потока отказов по данным испытаний и эксплуатации (см. МЭК 60050-191). Необходимость проверки таких предположений может возникнуть при проверке соответствия установленным требованиям или при оценке наличия изменений интенсивности отказов или параметра потока отказов во времени.
Методы, установленные в настоящем стандарте, предназначены для:
- проверки соответствия наработок до отказа невосстанавливаемых объектов экспоненциальному распределению, то есть постоянства интенсивности отказов;
- проверки наличия тренда наработок между отказами восстанавливаемого(ых) объекта(ов), то есть увеличения или уменьшения параметра потока отказов;
- построения графиков интенсивности отказов или параметра потока отказов, используемых для проверки предположения об их постоянстве, оценки их значения или идентификации характера их изменений.
2 Нормативные ссылки
В настоящем стандарте использованы нормативные ссылки на следующие стандарты:
МЭК 60050-191:1990 Международный электротехнический словарь. Глава 191. Надежность и качество услуг
МЭК 61649:1997 Критерии согласия, доверительные интервалы и нижние доверительные границы для распределения Вейбулла
МЭК 61710:2000 Степенная модель. Критерии согласия и методы оценки
3 Термины и определения
В настоящем стандарте применены термины по МЭК 60050-191 со следующими пояснениями и дополнениями:
a) термин «время» или «наработка» могут относиться к величинам, измеряемым в единицах длины, количества циклов или в других единицах;
b) событием, для которого в настоящем стандарте использован термин «отказ», может быть также другое установленное событие, например завершение ремонта объекта;
c) термин «интенсивность отказов» используется для обозначения мгновенной интенсивности отказов, называемой также функцией опасности;
d) приведенные методы применимы для данных о наработках между отказами, а также о наработках до отказа, собранных в процессе испытаний и эксплуатации объекта. В настоящем стандарте термин «испытания», используемый в разделах 6 и 7, может относиться как к испытаниям, так и к эксплуатации.
4 Обозначения
В настоящем стандарте применимы следующие обозначения:
i, j, k, l - индексы;
Hi - совокупная функция опасности в момент i-го отказа;
М(Тj) - среднее суммарное количество отказов за время Тj;
M(t) - среднее суммарное количество отказов на 100 систем;
m - количество уникальных наработок по всем восстанавливаемым объектам до отказа;
N(Ti) - количество объектов, за которыми ведется наблюдение в процессе испытаний или эксплуатации за время Тi;
Ni(Tj) - индикаторная переменная, равная 1, если отказ i-го объекта произошел за время Тj, и равная 0, если отказ i-го объекта не произошел за время Тj;
n - объем выборки; общее количество невосстанавливаемых объектов, подвергаемых испытаниям для проверки постоянства интенсивности отказов;
R(i, n) - вероятность безотказной работы объекта за время, равное i-й наработки ti, если наработки расположены в порядке неубывания, при объеме выборки n (используется в графическом методе при проверке постоянства интенсивности отказов);
Ri - вероятность безотказной работы объекта для i-го по порядку отказа;
r - количество отказов, произошедших в процессе испытаний;
r(Tj) - общее количество отказов за время Tj для многократно восстанавливаемых объектов;
ri(Tj) - количество отказов i-го объекта за время Тj;
rk - количество отказов k-го объекта в процессе испытаний;
Si - общее время испытаний для i-й наработки до отказа;
S0 - начальное значение общего времени испытаний S0 = 0;
Ti - суммарная наработка до i-го отказа;
Тr - общая суммарная наработка до r-го отказа;
Тij - суммарная наработка до j-го отказа i-го объекта;
Тj - упорядоченная (в порядке неубывания) суммарная наработка до j-го отказа Тj, Т1 < Т2 < ... < Тm;
Т* - общая суммарная наработка за время испытаний;
![]() - суммарная
наработка k-го
восстанавливаемого объекта за время испытаний;
- суммарная
наработка k-го
восстанавливаемого объекта за время испытаний;
ti - время, соответствующее i-му отказу объекта (используется при проведении испытаний п объектов для проверки постоянства интенсивности отказов);
t* - время завершения испытаний для проверки постоянства интенсивности отказов;
U - значение статистики, вычисленное по наблюдаемым значениям (используется при обработке данных испытаний для проверки постоянства интенсивности отказов);
Uα - квантиль уровня α нормированного нормального распределения;
Var(Тj) - дисперсия М(Тj) (используется при вычислении доверительного интервала);
Zi - нормализованное значение общего времени испытаний для i-го отказа;
α - вероятность ошибочного отклонения предположения о постоянстве интенсивности отказов или (мгновенного) параметра потока отказов, в то время как в действительности они являются постоянными (уровень значимости).
5 Требования
Для применения методов, установленных в настоящем стандарте, необходимо обеспечить выполнение следующих требований.
При испытаниях n невосстанавливаемых объектов для проверки предположения о постоянстве интенсивности отказов:
- для расчетных методов требуется не менее шести наработок до отказа;
- для графического метода требуется не менее четырех наработок до отказа.
При испытаниях одного или более восстанавливаемых объектов для проверки предположения о постоянстве параметра потока отказов:
- для расчетных методов требуется не менее шести наработок между отказами;
- для графического метода требуется не менее четырех наработок между отказами.
Примечание 1 - Для восстанавливаемых объектов предполагают, что время ремонта пренебрежимо мало.
Примечание 2 - В качестве расчетных методов приведены статистические критерии проверки постоянства интенсивности отказов и параметра потока отказов (см. 6.2, 7.2 и 7.3), а также методы определения для этих показателей доверительных интервалов (см. 7.4). Графические методы представляют собой изображение данных в виде графиков (см. разделы 6 и 7).
6 Критерий проверки постоянства интенсивности отказов
6.1 Общие замечания
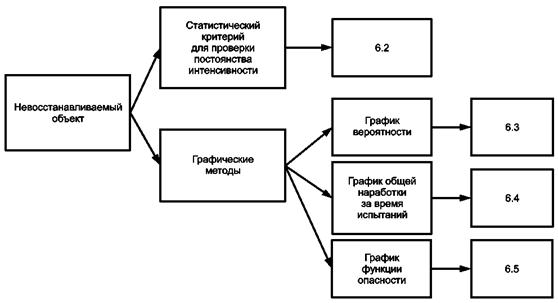
В настоящем стандарте приведены методы проверки постоянства интенсивности отказов для невосстанавливаемых объектов. Структура настоящего раздела изображена на рисунке 1.
Рисунок 1 - Структура раздела 6
Статистический критерий для проверки постоянства интенсивности отказов приведен для испытаний, завершаемых при достижении заданного времени, заданной наработки или заданного количества отказов.
В настоящем разделе рассмотрены три графических метода:
a) график вероятности основан на линейном преобразовании функции экспоненциального распределения. Его применяют, когда наработки до отказа известны для каждого невосстанавливаемого объекта или когда испытания всех объектов завершаются при достижении заданного времени наблюдений или заданного количества отказов.
b) график общей наработки за время испытаний (далее - графикТТТ1)) является эмпирическим и независимо от масштаба применим для данных, когда наработки до отказа известны для всех невосстанавливаемых объектов.
___________
1) ТТТ - Total time on test.
c) график функции опасности является линейным преобразованием совокупной функции опасности для экспоненциального распределения и применим в случае, когда наработки до отказа известны для каждого невосстанавливаемого объекта, а испытания завершаются при достижении заданного времени или заданного количества отказов, а также в случае, когда объекты были сняты с испытаний в произвольные моменты времени.
6.2 Статистический критерий для проверки постоянства интенсивности отказов
Описанный в настоящем подразделе метод применяют в том случае, когда испытаниям подвергают n объектов, а завершают испытания при достижении установленного количества отказов r (испытания с ограниченным количеством отказов) или установленного времени t (испытания с ограниченным временем наблюдений).
Внешние условия испытаний должны быть одинаковыми для всех объектов испытаний. При завершении испытаний не все объекты обязательно откажут. Таким образом, всего будет зафиксировано r наработок до отказа.
Шаг 1. Наработки до отказа располагают в порядке неубывания и обозначают упорядоченную выборку t1, t2, ..., tr.
Вычисляют суммарные наработки до i-го отказа для i от 1 до r.
![]()
Для испытаний с ограниченным временем наблюдений общую суммарную наработку к моменту r-го отказа вычисляют по формуле
![]()
Для испытаний с ограниченным количеством отказов общую суммарную наработку к моменту времени t* вычисляют по формуле
![]()
Шаг 2. Для каждой суммарной наработки Ti вычисляют статистику U по формуле
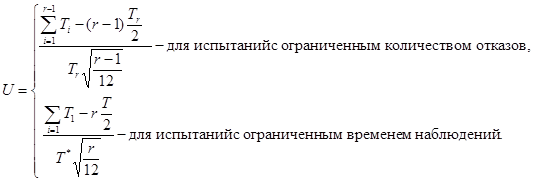
Шаг 3. Устанавливают уровень значимости α ошибочного отклонения предположения о постоянстве интенсивности отказов (в действительности интенсивность отказов является постоянной). Рекомендуемые значения α приведены в таблице 1.
Таблица 1 - Критическое значение Uα как функция α.
|
Критическое значение Uα |
|
|
0,025 |
2,24 |
|
0,050 |
1,96 |
|
0,100 |
1,64 |
Шаг 4. Предположение о постоянстве интенсивности отказов отклоняют в том случае, если абсолютное значение U больше критического значения, приведенного в таблице 1. В противном случае предположение о постоянстве интенсивности отказов не отклоняют.
Большие положительные значения U появляются при возрастании интенсивности отказов. И наоборот, большие отрицательные значения U появляются, когда интенсивность отказов уменьшается.
Метод применяют в случае, когда наработки до отказа известны для каждого невосстанавливаемого объекта и когда испытания завершаются в установленное время или при появлении установленного количества отказов.
Шаг 1. Упорядочивают наработки до отказа в порядке неубывания (от наименьшего до наибольшего), t1, t2, ..., tr.
Шаг 2. Вычисляют значение вспомогательной функции R(i, n), где i - индекс, соответствующий номеру наработки до отказа ti, a n - объем выборки, равный количеству невосстанавливаемых объектов испытаний
![]()
Примечание
- Следует отметить, что функция R(i, n) является оценкой
вероятности безотказной работы в момент времени, равный наработке до i-го отказа ti при испытаниях n объектов с постоянной
интенсивностью отказов, обычно ее обозначают ![]() .
Крышечка в обозначении
.
Крышечка в обозначении ![]() опущена,
поскольку в настоящем стандарте нет необходимости различать оценку и истинное
значение.
опущена,
поскольку в настоящем стандарте нет необходимости различать оценку и истинное
значение.
Шаг 3. Изображают график логарифма R(i, n) как функцию соответствующей наработки до отказа или график вспомогательной функции R(i, n) на логарифмической или полулогарифмической бумаге в логарифмическом или полулогарифмическом масштабе.
Примечание - Для построения графика вероятности экспоненциального закона используют специальную вероятностную бумагу.
Шаг 4. Если график функции представляет собой прямую линию, то нет оснований для отклонения предположения о постоянстве интенсивности отказов, а оценкой интенсивности отказов может быть абсолютное значение углового коэффициента этой прямой. В противном случае предположение о постоянстве интенсивности отказов должно быть отклонено.
6.4 График общей наработки за время испытаний
Метод применяют в случае, когда наработки до отказа известны для каждого невосстанавливаемого объекта испытаний.
Шаг 1. Наработки до отказов упорядочивают в порядке неубывания (от наименьшего до наибольшего) t1, t2, ..., tn, где t1 ≤ t2 ≤ ... ≤ tn.
Шаг 2. Вычисляют значения общих наработок за время испытаний (ТТТ) Si, i = 1, 2, ... n, соответствующих каждой наработке до отказа, считая S0 = 0
![]()
![]()
Шаг 3. Вычисляют нормализованные значения ТТТ Zi
![]()
Шаг
4. Изображают график нормализованных значений ТТТ Zi в зависимости
от доли объектов, отказавших за это время ![]() , i = 1, 2, ..., n, в линейном
масштабе и соединяют точки на графике с помощью отрезков прямой.
, i = 1, 2, ..., n, в линейном
масштабе и соединяют точки на графике с помощью отрезков прямой.
Шаг 5. Если график ТТТ представляет собой прямую линию, то нет оснований для отклонения предположения о постоянстве интенсивности отказов, а в качестве оценки интенсивности отказов можно использовать абсолютное значение углового коэффициента прямой. В противном случае предположение о постоянстве интенсивности отказов должно быть отклонено.
Метод применяют в случаях, когда наработки до отказа известны для каждого невосстанавливаемого объекта, а испытания всех объектов завершаются в установленное время или при достижении установленного количества отказов. Метод применяют в случае, когда данные испытаний включают в себя наработки до отказа невосстанавливаемых объектов и наработки не отказавших объектов, снятых с испытаний в произвольные моменты времени.
Шаг 1. Наработки располагают в порядке неубывания (от наименьшего до наибольшего) и обозначают i-ю наработку до отказа ti (t1 ≤ t2 ≤ ... ≤ ti ≤ ... ≤ tn).
Шаг 2. Вычисляют для всех наработок обратные ранги n, n - 1, n - 2, ..., 2, 1, где n - общее количество наработок. Обратный ранг i-й наработки вычисляют по формуле (n - i + 1).
Шаг 3. Вычисляют функцию опасности для каждой наработки как отношение 100 к соответствующему обратному рангу. Следовательно, функция опасности для i-й наработки равна
![]()
Шаг 4. Вычисляют совокупную функцию опасности Hi для каждой наработки как сумму функции опасности в i-й точке и предыдущей совокупной функции опасности.
Шаг 5. Изображают график совокупной функции опасности в зависимости от наработки до отказа в линейном масштабе.
Примечание 1 - На графике должны быть указаны только наработки до отказа, а не текущее время. Текущее время используют только при анализе графика.
Примечание 2 - Совокупную функцию опасности можно использовать для вычисления и построения графика вероятности безотказной работы Ri = ехр(-Hi).
Примечание 3 - Для построения графика функции опасности допускается использовать вероятностную (экспоненциальную) бумагу.
Шаг 6. Если график данной функции представляет собой прямую линию, то нет оснований для отклонений предположения о постоянстве интенсивности отказов, а в качестве интенсивности отказов может быть использовано абсолютное значение углового коэффициента прямой. В противном случае предположение о постоянстве интенсивности отказов должно быть отклонено.
Примечание - При проверке постоянства интенсивности отказов важен только угловой коэффициент прямой.
6.6 Действия в случае отклонения предположения о постоянстве интенсивности отказов
Если предположение о постоянстве интенсивности отказов отклонено, рекомендуется проанализировать данные для определения возможной причины. Результаты вычислений, если возможно, всегда должны сопровождаться физическими и техническими исследованиями.
Причинами изменения интенсивности отказов в рассматриваемом интервале времени могут быть износ или наличие процессов, приводящих к ранним отказам объектов. Возможно также, что данные не принадлежат к одной совокупности, а представляют собой смесь совокупностей с различными интенсивностями отказов, соответствующих различным видам отказов. Необходимо провести исследования всех вышеуказанных ситуаций.
В случае предположений о наличии износа или ранних отказов для невосстанавливаемых объектов необходимо использовать МЭК 61649, а для восстанавливаемых объектов - МЭК 61710. Если имеются предположения о наличии смеси совокупностей, должны быть предприняты меры по их идентификации и разделению. Затем совокупности следует проанализировать отдельно.
Независимо от причины отклонения предположения о постоянстве интенсивности отказов не следует применять методы, использующие эти предположения.
Примечание - Если предположение о постоянстве интенсивности отказов не отклонено, делают заключение: «не доказано, что распределение наработок до отказа отличается от экспоненциального распределения».
7 Критерий проверки постоянства параметра потока отказов
7.1 Общие замечания
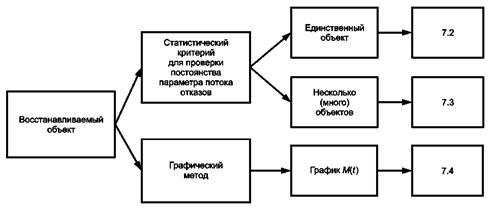
Объект относится к восстанавливаемым объектам. Результаты наблюдений представляют собой последовательность наработок между отказами. Методы проверки постоянства параметра потока отказов предполагают, что наработки между последовательными отказами не имеют тенденции ни к увеличению, ни к уменьшению. Если такая тенденция отсутствует, то объект испытаний после каждого ремонта можно рассматривать как новый. Структура настоящего раздела изображена на рисунке 2.
Рисунок 2 - Схема структуры раздела 7
В настоящем разделе приведены два формальных статистических критерия проверки постоянства параметра потока отказов:
a) единственный восстанавливаемый объект, соответствующий единственной системе или нескольким идентичным системам, функционирующим в идентичных условиях;
b) несколько восстанавливаемых объектов, соответствующих нескольким системам одного вида, функционирующим в различных условиях.
Графический метод предназначен для одного или более восстанавливаемых объектов, даже если данные были получены в течение различных периодов времени.
Примечание - Параметр потока отказов сложной большой системы может быть постоянным, даже если ее составные части не имеют постоянных интенсивностей отказов. Например, параметр потока отказов может быть практически постоянным для ремонтируемого объекта, даже если компоненты объекта подвержены изнашиванию.
Данный расчетный метод применим при наличии не менее шести последовательных наработок между отказами, зарегистрированных за время испытаний T*.
Шаг 1. Для восстанавливаемого объекта суммарная наработка до i-го отказа равна Ti. Метод применим также для последней наработки Тr, и любой другой большей наработки T*, в процессе которой объект продолжал функционировать.
Примечание - Для наработки между последовательными отказами справедливо соотношение ti = Ti - Ti - 1.
Шаг 2. Для каждой суммарной наработки Ti вычисляют статистику U по формуле
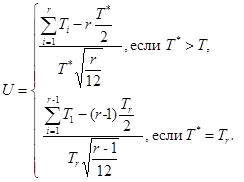
Шаг 3. Назначают уровень значимости α для ошибочного отклонения предположения о постоянстве параметра потока отказов. Рекомендуемые значения α приведены в таблице 1.
Шаг 4. Если абсолютное значение U больше критического значения, приведенного в таблице 1, предположение о постоянстве параметра потока отказов отклоняют. В противном случае это предположение не отклоняют.
Если параметр потока отказов является постоянным, статистика U подчиняется нормированному нормальному распределению. Большие абсолютные значения U являются основанием для отклонения предположения о постоянстве параметра потока отказов.
Большие положительные значения U появляются в тех случаях, когда существует тенденция к уменьшению наработок между последовательными отказами. Наоборот, большие отрицательные значения U появляются в тех случаях, когда наработки имеют тенденцию к увеличению, что соответствует уменьшению параметра потока отказов.
Примечание - Неотклонение предположения о постоянстве параметра потока отказов не следует интерпретировать как соответствие наработок между последовательными отказами восстанавливаемого объекта экспоненциальному распределению. Единственное заключение, которое можно сделать в этом случае, это то, что наличие тренда наработок не доказано. Несмотря на то, что предположение о постоянстве параметра потока отказов не противоречит экспоненциальному распределению наработок между отказами, наработки могут подчиняться другому распределению, имеющему тренд параметра потока отказов.
7.3 Критерий проверки постоянства параметра потока отказов нескольких восстанавливаемых объектов
Данный метод является расширением метода, описанного в 7.2. Если имеются данные для нескольких восстанавливаемых объектов, соответственно проверяют постоянство параметра потока отказов каждого объекта.
Шаг 1. Для каждого объекта фиксируют суммарную наработку за весь период наблюдений, общее количество наблюдаемых отказов и соответствующие им наработки (см. таблицу 2).
Таблица 2 - Вычисление наработок до отказа нескольких восстанавливаемых объектов
|
Суммарная наработка за весь
период наблюдения |
Общее количество отказов за весь период наблюдений ri |
Момент возникновения отказа j = 1, 2, ..., ri |
|
|
1 |
|
r1 |
T1j |
|
2 |
|
r2 |
T2j |
|
3 |
|
r3 |
T3j |
|
... |
... |
... |
... |
|
k |
|
rk |
Tkj |
|
Примечание - Если испытания некоторых объектов проводились до r-го отказа, то для этого объекта устанавливают T* = Tr и r = r - 1. |
|||
Шаг 2. Вычисляют статистику U по формуле
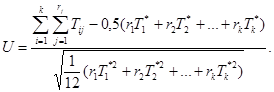
Шаг 3. Устанавливают уровень значимости α для ошибочного отклонения предположения о постоянстве параметра потока отказов при условии, что в действительности он является постоянным. Рекомендуемые значения α приведены в таблице 1.
Шаг 4. Предположение о постоянстве параметра потока отказов для всех идентичных объектов отклоняют в том случае, если абсолютное значение U больше критического значения, приведенного в таблице 1. В противном случае предположение не отклоняют.
В соответствии с предположением об отсутствии тренда, т.е. о постоянстве параметра потока отказов в течение продолжительного периода времени, статистика U подчиняется нормированному нормальному распределению. Большие абсолютные значения U являются основанием для отклонения данного предположения.
Большие положительные значения U появляются при наличии тенденции к уменьшению наработок между последовательными отказами в любом из идентичных объектов. Наоборот, большие отрицательные значения U появляются в том случае, когда эти наработки имеют тенденцию к увеличению, т.е. параметр потока отказов уменьшается хотя бы в одном из идентичных объектов.
Примечание - Неотклонение предположения о постоянстве параметра потока отказов означает только то, что нет достаточно веских оснований для отклонения предположения о постоянстве параметров потока отказов всех идентичных объектов.
7.4 График M(t)
Данный графический метод применяют при наличии данных для одного или большего количества восстанавливаемых объектов, даже если наблюдения за ними проводились в течение различных периодов времени. График M(t) позволяет идентифицировать характер тренда параметра потока отказов. Метод может помочь установить постоянство параметра потока отказов и применяется как дополнение к расчетным методам, приведенным в 7.2 и 7.3. Построение графика M(t) позволяет также идентифицировать другие особенности параметра потока отказов, такие как отказы на ранних этапах эксплуатации объекта.
Примечание - График M(t) позволяет проводить эмпирический анализ наблюдаемых отказов для восстанавливаемых объектов. Он не требует наличия предположений о форме основного процесса, из которого получены данные. Анализ графика M(t) является простым средством идентификации характера параметра потока отказов, применимым в общем случае для нескольких восстанавливаемых объектов, и может быть полезным для выявления отклонений от постоянства параметра потока отказов.
Шаг 1. Упорядочивают суммарные наработки до j-го отказа i-го объекта Tij в порядке неубывания, где i = 1, 2, ..., k.
Шаг 2. Идентифицируют m - количество уникальных (различных по величине) суммарных наработок до отказа.
Шаг 3. Обозначают упорядоченные уникальные суммарные наработки до j-го отказа по всем объектам Тj, (j = 0, 1, ..., m), T1 < Т2 < ... Тm.
Шаг 4. Вычисляют ri (Тj) - количество отказов i-го объекта за суммарную наработку Тj.
Шаг 5. Определяют значение индикаторной переменной Ni(Тj), которая равна 1, если наблюдения за i-м объектом проводились в момент времени Тj, и равна 0, если наблюдения за i-м объектом в момент времени Тj не проводились.
Шаг 6. Вычисляют среднее суммарное количество наработок до отказа за время Тj.
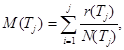
где ![]()
![]()
Шаг 7. Строит график M(Tj), (j = 0, 1, ..., m)
Шаг 8. Постоянный параметр потока отказов соответствует линейному характеру графика. Любое отклонение от прямой линии указывает на то, что параметр потока отказов не постоянен.
Шаг 9. Границы двустороннего доверительного интервала M(Tj) определяют по следующей формуле
![]()
где Uα/2 - квантиль уровня α/2 нормированного нормального распределения, соответствующий уровню доверия 100(1 - α) %. Рекомендуемые значения α приведены в таблице 3.
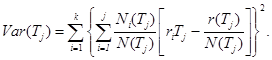
7.5 Действия в случае отклонения предположения о постоянстве параметра потока отказов
Если критерий проверки постоянства параметра потока отказов отклоняет это предположение, следовательно, параметр потока отказов или увеличивается, или уменьшается. Это означает, что вероятность безотказной работы после каждого ремонта увеличивается или уменьшается. Расчетные методы для моделирования этой ситуации приведены в МЭК 61710.
Таблица 3 - Квантили нормированного нормального распределения
|
100(1 - α ) % |
Uα/2 |
|
99 % |
2,58 |
|
95 % |
1,96 |
|
90 % |
1,64 |
Приложение А
(справочное)
Примеры применения настоящего стандарта
А.1 Проверка постоянства интенсивности отказов для невосстанавливаемого объекта
Сорок объектов поставлены на испытания в одно и то же время. Испытания были завершены после появления 20-го отказа. В таблице А.1 приведены упорядоченные наработки до отказа 20 отказавших объектов. Для проверки постоянства интенсивности отказов использован метод, приведенный в 6.2.
Таблица А.1 - Упорядоченные наработки до отказа 20 отказавших объектов
|
ti |
i |
ti |
i |
ti |
|
|
1 |
5 |
8 |
36 |
15 |
64 |
|
2 |
10 |
9 |
54 |
16 |
65 |
|
3 |
17 |
10 |
55 |
17 |
65 |
|
4 |
32 |
11 |
55 |
18 |
66 |
|
5 |
32 |
12 |
58 |
19 |
67 |
|
6 |
33 |
13 |
58 |
20 |
68 |
|
7 |
34 |
14 |
61 |
Шаг 1. Наработки до отказа располагают в порядке неубывания и определяют суммарные наработки до i-го отказа (см. таблицу А.2).
Таблица А.2 - Суммарные наработки до отказа 20 объектов
|
ti |
Ti |
i |
ti |
Ti |
|
|
1 |
5 |
200 |
11 |
55 |
1958 |
|
2 |
10 |
395 |
12 |
58 |
2045 |
|
3 |
17 |
661 |
13 |
58 |
2045 |
|
4 |
32 |
1216 |
14 |
61 |
2126 |
|
5 |
32 |
1216 |
15 |
64 |
2204 |
|
6 |
33 |
1251 |
16 |
65 |
2229 |
|
7 |
34 |
1285 |
17 |
65 |
2229 |
|
8 |
36 |
1351 |
18 |
66 |
2252 |
|
9 |
54 |
1927 |
19 |
67 |
2274 |
|
10 |
55 |
1958 |
20 |
68 |
2295 |
Данные испытания являются испытаниями с ограниченным количеством отказов, следовательно, Тr = 2295.
Шаг 2. Вычисляют значение статистики U по формуле
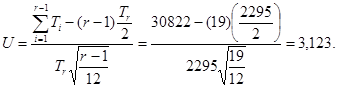
Шаги 3 и 4. Для уровня значимости α = 10 % статистика U превышает критическое значение Uα = 1,64 (см. таблицу 1), поэтому предположение о постоянстве интенсивности отказов отклоняют. Положительное значение статистики U указывает на увеличение интенсивности отказов.
А.2 Проверка постоянства интенсивности отказов для невосстанавливаемых объектов
В процессе испытаний фиксировались наработки до отказа компонентов системы. На испытания было поставлено двенадцать компонентов. Наблюдения прекращены после появления 12-го отказа. Наработки до отказа приведены в таблице А.3. Для проверки постоянства интенсивности отказов был использован метод, приведенный в 6.2.
Таблица А.3 - Наработки до отказа компонентов, расположенные в порядке неубывания
|
2 |
5 |
6 |
7 |
11 |
16 |
20 |
20 |
21 |
23 |
32 |
Шаг 1. Результаты вычисления суммарных наработок до отказа приведены в таблице А.4.
Таблица А.4 - Суммарные наработки до отказа
|
ti |
Ti |
i |
ti |
Ti |
|
|
1 |
1 |
1 |
7 |
16 |
48 |
|
2 |
2 |
3 |
8 |
20 |
68 |
|
3 |
5 |
8 |
9 |
20 |
88 |
|
4 |
6 |
14 |
10 |
21 |
109 |
|
5 |
7 |
21 |
11 |
23 |
132 |
|
6 |
11 |
32 |
12 |
32 |
164 |
Шаг 2. Вычисляют значение статистики U по формуле
![]()
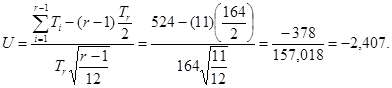
Шаги 3 и 4. Для уровня значимости α = 5 % абсолютное значение статистики превышает критическое значение Uα = 1,96 (см. таблицу 1), поэтому предположение о постоянстве интенсивности отказов отклоняют. Отрицательное значение статистики указывает на уменьшение интенсивности отказов.
А.3 Проверка постоянства параметра потока отказов для единственного восстанавливаемого объекта
Единственный объект был подвергнут испытаниям в течение 6 мес (T* = 4380 ч). За время испытаний зафиксировано восемь отказов объекта, которые произошли в моменты времени Тi. Значения Тi приведены в таблице А.5. Для проверки постоянства параметра потока отказов был использован метод, приведенный в 7.2.
Таблица А.5 - Моменты отказа объекта испытаний
|
Ti |
i |
Ti |
|
|
1 |
25 |
5 |
835 |
|
2 |
94 |
6 |
1279 |
|
3 |
282 |
7 |
2048 |
|
4 |
384 |
8 |
3253 |
Шаг 1. Рассчитанные суммарные наработки до отказа приведены в таблице А.6.
Таблица А.6 - Суммарные наработки до отказа
|
Ti |
i |
Ti |
|
|
1 |
25 |
5 |
835 |
|
2 |
94 |
6 |
1279 |
|
3 |
282 |
7 |
2048 |
|
4 |
384 |
8 |
3253 |
Шаг 2. Вычисляют значение статистики U по формуле
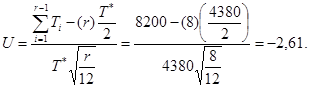
Шаги 3 и 4. Для уровня значимости α = 10 % абсолютное значение статистики превышает критическое значение Uα = 1,64 (см. таблицу 1), поэтому предположение о постоянстве параметра потока отказов отклоняют. Отрицательное значение статистики указывает на уменьшение параметра потока отказов.
А.4 Проверка постоянства параметра потока отказов для нескольких восстанавливаемых объектов
На испытания поставлены три идентичных восстанавливаемых объекта. Данные об отказах приведены в таблице А.7. Для проверки постоянства параметра потока отказов был использован метод, приведенный в 7.3.
Таблица А.7 - Данные об отказах для трех восстанавливаемых объектов
|
Суммарная наработка до отказа |
Суммарная наработка за время испытаний |
|
|
1 |
5, 8 |
12 |
|
2 |
- |
16 |
|
3 |
1, 8, 16 |
20 |
Шаг 1. За время испытаний вычисляют суммарную наработку для каждого объекта, общее количество наблюдаемых отказов и соответствующие наработки (таблица А.8).
Таблица А.8 - Рабочая таблица вычислений
|
Объект i |
Суммарная наработка за время
испытаний |
Общее количество отказов rj |
Наработка, соответствующая j-му отказу i-го объекта Тij |
|
||
|
1 |
12 |
2 |
5 |
8 |
- |
13 |
|
2 |
16 |
0 |
- |
- |
- |
0 |
|
3 |
20 |
3 |
1 |
8 |
16 |
25 |
Шаг 2. Вычисляют статистику U по формуле
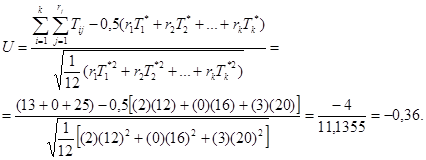
Шаги 3 и 4. Для уровня значимости α = 10 % абсолютное значение статистики не превышает критического значения Uα = 1,64 (см. таблицу 1), поэтому предположение о постоянстве параметра потока отказов не может быть отклонено.
А.5 График вероятности для проверки постоянства интенсивности отказов
Упорядоченные наработки до отказа восьми из десяти объектов приведены в таблице А.9. Испытания с ограниченным временем наблюдений продолжались в течение 1500 ч. Для проверки постоянства интенсивности отказов был использован метод, приведенный в 6.3.
Таблица А.9 - Наработки до отказа невосстанавливаемых объектов
|
ti |
i |
ti |
|
|
1 |
104 |
6 |
760 |
|
2 |
210 |
7 |
1100 |
|
3 |
400 |
8 |
1200 |
|
4 |
460 |
9 |
1500 |
|
5 |
630 |
10 |
1500 |
Шаг 1. Упорядоченные наработки до отказа приведены в графе 2 таблицы А.10.
Шаг 2. Результаты вычисления вспомогательной функции R(i, n) приведены в графе 4 таблицы А.10.
Таблица А.10 - Рабочая таблица вычислений
|
Наработка до отказа Тi |
Режим |
Вероятность безотказной работы R(i, n) |
Логарифм вероятности безотказной работы - lnR(i, n) |
|
|
1 |
2 |
3 |
4 |
5 |
|
1 |
104 |
Отказ |
0,9327 |
0,0697 |
|
2 |
210 |
Отказ |
0,8365 |
0,1785 |
|
3 |
400 |
Отказ |
0,7404 |
0,3006 |
|
4 |
460 |
Отказ |
0,6442 |
0,4397 |
|
5 |
630 |
Отказ |
0,5481 |
0,6013 |
|
6 |
760 |
Отказ |
0,4519 |
0,7942 |
|
7 |
1100 |
Отказ |
0,3558 |
1,0335 |
|
8 |
1200 |
Отказ |
0,2596 |
1,3486 |
|
9 |
1500 |
Работоспособное состояние |
||
|
10 |
1500 |
Работоспособное состояние |
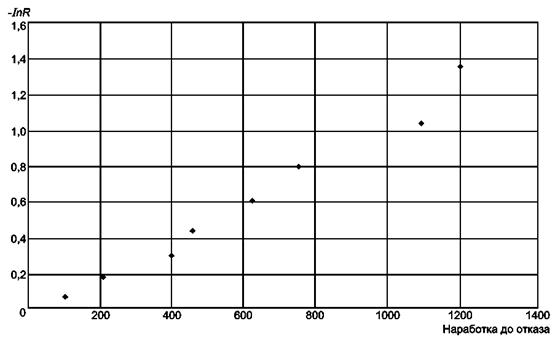
Шаг 3. График - lnR(i, n) как функция соответствующего момента отказа приведен на рисунке А.1.
Шаг 4. График представляет собой практически прямую линию, поэтому нет оснований для отклонения предположения о постоянстве интенсивности отказов.
Примечание - Примеры, приведенные в настоящем приложении, демонстрируют применение методов, установленных в настоящем стандарте. В стандарте не установлен метод графического анализа с применением статистических критериев согласия, так как стандарт направлен на применение эмпирических методов, используемых на практике.
Рисунок А.1 - График вероятности для проверки постоянства интенсивности отказов
А.6 График совокупной функции опасности для проверки постоянства интенсивности отказов
Данные, полученные после проведения ускоренных испытаний 10 электронных модулей, приведены в таблице А.11. Для анализа были использованы только отказы. Для проверки постоянства интенсивности отказов и определения оценки интенсивности отказов был использован метод, приведенный в 6.5.
Таблица А.11 - Десять упорядоченных наработок двух видов отказов
|
Время ti |
Вид отказа |
|
|
1 |
104 |
А |
|
2 |
210 |
А |
|
3 |
400 |
В |
|
4 |
460 |
А |
|
5 |
630 |
А |
|
6 |
760 |
А |
|
7 |
1100 |
А |
|
8 |
1200 |
В |
|
9 |
1500 |
Цензурирование |
|
10 |
1500 |
Цензурирование |
Шаг 1. В таблице А.12 приведены упорядоченные наработки и рабочая таблица результатов вычислений.
Шаг 2. Обратные ранги всех наработок приведены в графе 3 таблицы А.12.
Шаг 3. Совокупная функция опасности в каждой точке отказа приведена в графе 5 таблицы А.12.
Шаг 4. Так как рассматриваются отказы вида А, совокупная функция опасности вычислена только для данных отказов (см. графу 6 таблицы А.12). Пустые строки соответствуют отказам вида В и точкам цензурирования.
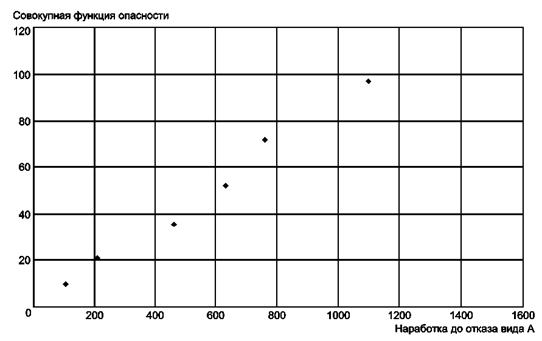
Шаг 5. На рисунке А.2 изображен график совокупной функции опасности в зависимости от наработок.
Шаг 6. Поскольку график представляет собой практически прямую линию, следовательно, нет оснований для отклонения предположения о постоянстве интенсивности отказов. Оценка интенсивности отказов равна угловому коэффициенту этой прямой и составляет 0,000882. В графе 7 таблицы А.12. приведены результаты вычисления вероятности безотказной работы Ri = exp(-Hi), которые при необходимости можно использовать для построения графика вероятности.
Таблица А.12 - Рабочая таблица вычислений
|
Время ti |
Обратный ранг |
Вид отказа |
Функция опасности, % |
Совокупная функция опасности Hi, % |
Вероятность безотказной работы Ri, % |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
1 |
104 |
10 |
А |
10,00 |
10,00 |
90,48 |
|
2 |
210 |
9 |
А |
11,11 |
21,11 |
80,97 |
|
3 |
400 |
8 |
В |
12,50 |
||
|
4 |
460 |
7 |
А |
14,29 |
35,40 |
70,19 |
|
5 |
630 |
6 |
А |
16,67 |
52,07 |
59,41 |
|
6 |
760 |
5 |
А |
20,00 |
72,07 |
48,64 |
|
7 |
1100 |
4 |
А |
25,00 |
97,07 |
37,88 |
|
8 |
1200 |
3 |
В |
33,33 |
||
|
9 |
1500 |
2 |
Цензурирование |
50,00 |
||
|
10 |
1500 |
1 |
Цензурирование |
100,00 |
Рисунок А.2 - График совокупной функции опасности
А.7 График M(t) для восстанавливаемых объектов
В процессе испытаний трех восстанавливаемых объектов зафиксированы отказы, данные о которых приведены в таблице А.13.
Таблица А.13 - Наработки трех идентичных восстанавливаемых объектов
|
Суммарная наработка до отказа |
Суммарная наработка за время испытаний |
|
|
1 |
4, 9 |
12 |
|
2 |
16 |
|
|
3 |
1, 9, 15 |
20 |
Для проверки постоянства параметра потока отказов был использован метод, приведенный в 7.4.
Шаг 1. Упорядоченные суммарные наработки до отказа по всем идентичным объектам: 1, 4, 9, 9, 15.
Шаг 2. В результате испытаний получено четыре уникальные (различные по величине) суммарные наработки до отказа.
Шаг 3. Четыре уникальные суммарные наработки до отказа, расположенные в порядке неубывания: 1, 4, 9, 15.
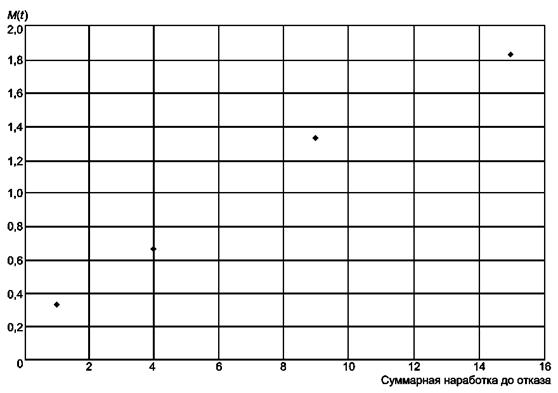
Шаги 4 - 6. Результаты вычислений M(Tj) приведены в таблице А.14.
Таблица А.14 - Рабочая таблица вычислений M(t)
|
Шаг 3 |
Шаг 4 |
Шаг 5 |
Шаг 6 |
|||||||
|
j |
Tj |
r1(Tj) |
r2(Tj) |
r3(Tj) |
N1(Tj) |
N2(Tj) |
N3(Tj) |
r(Tj) |
N(Tj) |
M(Tj) |
|
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
3 |
0,3333 |
|
2 |
4 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
3 |
0,6667 |
|
3 |
9 |
1 |
0 |
1 |
1 |
1 |
1 |
2 |
3 |
1,3333 |
|
4 |
15 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
2 |
1,8333 |
Шаг 7. График М(Tj) как функции Tj, j = 0, 1, ..., m изображен на рисунке А.3.
Шаг 8. График представляет собой практически прямую линию, следовательно, нет оснований для отклонения предположения о постоянстве параметра потока отказов.
Шаг 9. Рабочая таблица вычислений дисперсии и доверительного интервала для M(t) приведена в таблице А.15.
Рисунок А.3 - График M(t) для трех восстанавливаемых объектов
Таблица А.15 - Рабочая таблица вычисления дисперсии и доверительных интервалов для M(t)
|
Tj |
Объект 1 |
Объект 2 |
Объект 3 |
|
|
|
1 |
1 |
1/3(0 - 1/3) = - 0,1111 |
1/3(0 - 1/3) = -0,1111 |
1/3(1 - 1/3) = 0,2222 |
0,0741 |
|
2 |
4 |
1/3(1 - 1/3) = 0,2222 |
1/3(0 - 1/3) = -0,1111 |
1/3(0 - 1/3) = -0,1111 |
0,0741 |
|
3 |
9 |
1/3(1 - 2/3) = 0,1111 |
1/3(0 - 2/3) = -0,2222 |
1/3(1 - 2/3) = 0,1111 |
0,2963 |
|
4 |
15 |
0/2(0 - 1/2) = 0,0000 |
1/2(0 - 1/2) = -0,2500 |
1/2(1 - 1/2) = 0,2500 |
0,7546 |
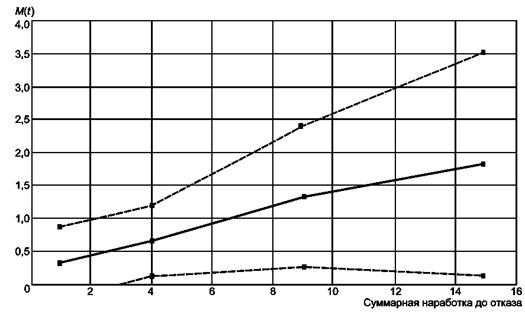
Таким образом, для уровня доверия 95 % доверительные границы M(t) имеют вид
![]()
Значения доверительных границ приведены в таблице А.16.
Таблица А.16 - Доверительные границы для M(t)
|
Tj |
M(Tj) |
Нижняя доверительная граница для уровня доверия 95 % |
Верхняя доверительная граница для уровня доверия 95 % |
|
|
1 |
1 |
0,3333 |
-0,2001 |
0,8668 |
|
2 |
4 |
0,6667 |
0,1332 |
1,2001 |
|
3 |
9 |
1,3333 |
0,2664 |
2,4002 |
|
4 |
15 |
1,8333 |
0,1307 |
3,5360 |
График M(t) с границами доверительного интервала для уровня доверия 95 % изображен на рисунке А.4.
![]() - среднее совокупное количество отказов за наработку
M(t);
- среднее совокупное количество отказов за наработку
M(t);
![]() - нижняя доверительная граница M(t) для уровня доверия 95 %;
- нижняя доверительная граница M(t) для уровня доверия 95 %;
![]() - верхняя доверительная граница M(t) для уровня доверия 95 %.
- верхняя доверительная граница M(t) для уровня доверия 95 %.
Рисунок А.4 - График M(t) доверительного интервала с уровнем доверия 95 %
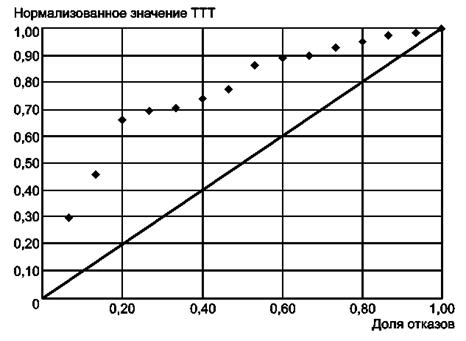
А.8 ТТТ - график для проверки постоянства интенсивности отказов
Наработки до отказа пятнадцати идентичных компонентов, зафиксированные в процессе испытаний, приведены в таблице А.17.
Таблица А.17 - Наработки до отказа
|
1006 |
426 |
794 |
270 |
1512 |
1019 |
742 |
681 |
696 |
1289 |
1172 |
643 |
1093 |
1366 |
Для проверки постоянства интенсивности отказов был использован метод, приведенный в 6.4.
Шаг 1. Упорядоченные наработки до отказа приведены в графе 2 таблицы А.18.
Шаг 2. Значения ТТТ за время испытаний приведены в графе 3 таблицы А.18.
Шаг 3. Нормализованные значения ТТТ приведены в графе 4 таблицы А.18.
Шаг 4. На рисунке А.5 показан график значений Zi - как функции доли отказавших за соответствующую наработку объектов - i/n(i = 1, 2, ..., n).
Шаг 5. График ТТТ является нелинейным. Это означает, что есть основания для отклонения предположения о постоянстве интенсивности отказов. Впадина на графике говорит о наличии периода роста интенсивности отказов.
Таблица А.18 - Рабочая таблица вычислений
|
Наработка ti |
Значение Si |
Нормализованное значение ТТТ Zi |
Отношение |
|
|
1 |
2 |
3 |
4 |
5 |
|
1 |
270 |
4050 |
0,30 |
0,07 |
|
2 |
426 |
6234 |
0,46 |
0,13 |
|
3 |
643 |
9055 |
0,66 |
0,20 |
|
4 |
681 |
9511 |
0,70 |
0,27 |
|
5 |
696 |
9676 |
0,71 |
0,33 |
|
6 |
742 |
10136 |
0,74 |
0,40 |
|
7 |
794 |
10604 |
0,78 |
0,47 |
|
8 |
945 |
11812 |
0,87 |
0,53 |
|
9 |
1006 |
12239 |
0,90 |
0,60 |
|
10 |
1019 |
12317 |
0,90 |
0,67 |
|
11 |
1093 |
12687 |
0,93 |
0,73 |
|
12 |
1172 |
13003 |
0,95 |
0,80 |
|
13 |
1289 |
13354 |
0,98 |
0,87 |
|
14 |
1366 |
13508 |
0,99 |
0,93 |
|
15 |
1512 |
13654 |
1,00 |
1,00 |
Рисунок А.5 - График ТТТ для проверки постоянства интенсивности отказов
Приложение В
(справочное)
Пример анализа M(t) для данных эксплуатации
Потребительский товар (мобильный телефон) продается в большом количестве. Каждый телефон имеет регистрационный номер. Невозможно зарегистрировать время продажи или начало эксплуатации телефона, так как остаются запасы данного товара у дистрибьюторов и в пунктах продаж. Кроме того, невозможно определить количество изъятых телефонов, так как некоторое их количество может быть реэкспортировано из страны, где они были первоначально проданы. Кроме того, неизвестно количество выброшенных телефонов.
Изготовитель определяет количество телефонов на рынке, поступивших из производства и коммерческих структур, не учитывая выброшенные и экспортируемые телефоны. Этот приближенный метод расчета применим в течение первых нескольких лет наличия телефона на рынке. Проблема с запасами товара у дистрибьюторов в пунктах продаж может быть решена путем анализа партий согласно С.6 приложения С.
Исследование надежности телефона проводилось только на одном рынке. Было достигнуто соглашение с магазинами, выполняющими ремонт телефонов, о том, что все даты ремонта они будут сообщать изготовителю данной модели телефона. Поставка данных о ремонте необходима для оплаты магазину компенсации по гарантийному ремонту. Полученные из магазина данные о ремонте включают в себя регистрационный номер каждого восстановленного телефона, претензию потребителя, тип отказа и вид выполненного ремонта (перечень замененных отказавших компонентов). Дату, когда телефон поступил в ремонт, регистрируют. По номеру серии телефона изготовитель может определить дату его изготовления и, зная среднее время распределения и продажи, может оценить вероятную дату начала эксплуатации телефона. Вычитая дату начала эксплуатации из даты поступления на ремонт можно оценить время эксплуатации в днях. Поскольку в телефоне не предусмотрен автоматический учет времени эксплуатации, количество рабочих часов оценить невозможно. Поэтому было принято решение измерять время эксплуатации в днях, а не в часах.
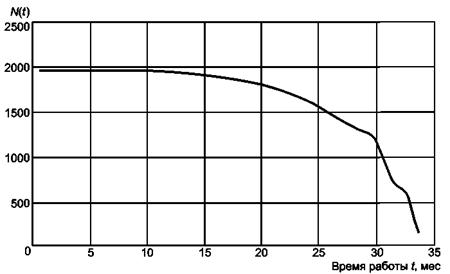
Общее количество телефонов, находящихся в эксплуатации, изображено в виде графика на рисунке В.1. В течение некоторого времени это количество является постоянным и составляет 1966 телефонов. Продажа этой модели закончилась. Первые телефоны, которые поступили на рынок, были произведены 33,5 мес. назад (2,8 г.), а последний - 10 мес. назад.
Рисунок В.1 - Общее количество систем как функция времени эксплуатации
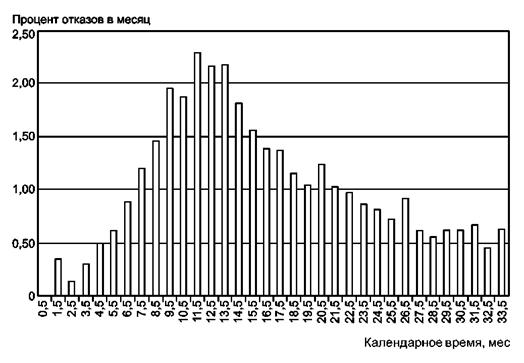
Сначала изготовитель определяет количество ежемесячно проведенных ремонтов, а затем делит его на общее количество изготовленных телефонов. Полученный график приведен на рисунке В.2. Можно заметить, что процент отказов телефонов в течение месяца колеблется, даже если в телефон не было внесено никаких изменений. Колебания процента отказов вызваны:
a) отклонениями при выполнении ремонта;
b) изменением объема продаж, появлением ранних отказов.
Поэтому эти статистические данные не подходят для принятия административных решений или действий по улучшению.
Рисунок В.2 - Количество ремонтов за месяц как доля совокупности
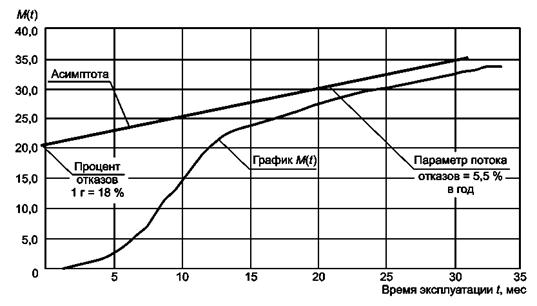
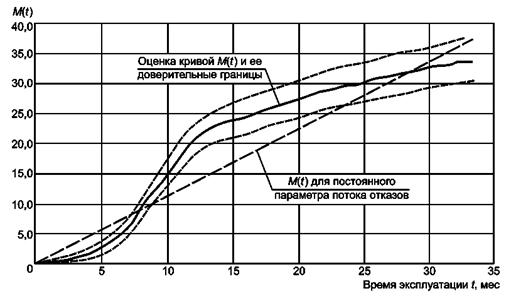
Вместо вычисления интенсивности отказов (например, процента отказов за месяц) строят совокупную кривую в виде графика M(t), приведенного на рисунках В.3 и В.4 с доверительными границами для уровня доверия 99 %. Анализ графика показал, что проблема вызвана ранними отказами. Поэтому на предприятии-изготовителе были предприняты действия для уменьшения ранних отказов. Однако базовая конструкция является приемлемой для времени, на которое рассчитана данная продукция. Можно заметить, что телефоны поступали на сервисное обслуживание последовательно в течение первых 5 мес. Ранние отказы появлялись приблизительно через 7 - 13 мес. эксплуатации.
Рисунок В.3 - График M(t)
Рисунок В.4 - Кривая M(t) с доверительными границами для уровня доверия 99 %
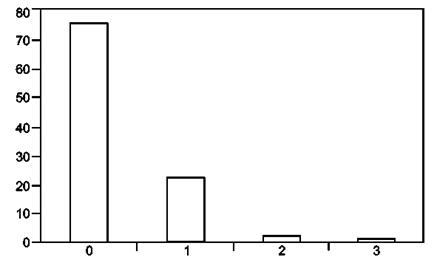
Для того чтобы подтвердить, что основной причиной являются ранние отказы, количество проведенных ремонтов телефонов отражено на графике, изображенном на рисунке В.5. На графике видно, что 75 % телефонов никогда не ремонтировались, 22 % ремонтировались один раз, 2 % подвергались ремонту дважды. Только 1 % телефонов подвергался ремонту более двух раз. Этот анализ позволяет изготовителю прекратить проверку, если телефон был отремонтирован до наступления вычисленной наработки до отказа/между отказами. Это упрощает анализ, так как только данные изготовителя могут быть использованы для вычислений.
Количество ремонтов
![]() Процент
телефонов
Процент
телефонов
Рисунок В.5 - Количество ремонтов телефонов
На рисунке В.3 видно, что отказы начинают появляться после некоторого времени эксплуатации, их количество медленно увеличивается, поскольку потребители сдают телефоны в ремонт. Оценка параметра потока отказов составляет 5,5 % в год после 15 мес. эксплуатации. Процент отказов в течение первого года (гарантия) - 18 %.
Приложение С
(справочное)
Подготовка данных эксплуатации для анализа M(t)
С.1 Методы анализа данных эксплуатации
Метод построения графика M(t), приведенный в настоящем стандарте, может использоваться для идентификации периодов постоянного параметра потока отказов по данным эксплуатации. Метод позволяет идентифицировать периоды ранних отказов и определить процент ранних отказов. Кроме того, метод позволяет идентифицировать периоды износа и определить наработки до отказа и параметр потока отказов при предположении, что он постоянен.
Часто организации хотят вести мониторинг появления отказов в эксплуатации для оценки затрат в течение гарантийного периода, а также для накопления информации о надежности и повышении надежности объектов, находящихся в эксплуатации.
С.2 Количество отказов за период времени
Часто организации анализируют статистику о количестве отказов за указанный период времени, например за месяц. Для этого необходимо определить количество отказов за каждый такой период времени. Однако такой анализ часто вводит в заблуждение, так как в нем не учитывается количество объектов, находящихся в эксплуатации. Этот параметр часто называют совокупностью в эксплуатации или совокупностью в состоянии риска (PAR1)).
______________
1) PAR - Population at risk. 22
С.3 Процент отказов за период времени
Когда PAR изменяется, количество ремонтов делят на объем совокупности в эксплуатации и определяют процент отказов за указанный период времени.
Примечание - Процент отказов за период времени часто называют заявленной интенсивностью.
Чтобы выполнить эти расчеты, организация должна определить количество проведенных ремонтов или претензии за каждый период времени (например, за каждый месяц) и количество объектов, находящихся в эксплуатации в этом же месяце (совокупность в эксплуатации, т.е. PAR). Значит PAR может быть вычислена путем прибавления количества объектов, находящихся на обслуживании, к количеству объектов, находящихся в эксплуатации, и вычитания количества объектов, изъятых из использования (утилизированных). Оценить количество объектов, изъятых из использования, часто является сложной задачей, так как они могут быть проданы другому пользователю. Иногда трудно также определить, когда объект был поставлен на обслуживание. Для более точного определения времени предъявления на ремонт часто используют дату поставки или дату продажи. Если время, когда объект находится на хранении или у дистрибьютора, является очень незначительным, дата изготовления может быть использована как оценка даты постановки продукции на обслуживание. Поэтому совокупность в использовании часто можно определить приблизительно так:
PAR = объекты, поставленные на рынок, + объекты, проданные в течение рассматриваемого периода времени, - объекты, изъятые в течение рассматриваемого периода времени.
Так как организацию главным образом интересует статистика данных эксплуатации в течение гарантийного периода времени, неопределенность, вызванная изъятием, часто имеет меньшее значение.
Если параметр потока отказов продукции является постоянным во времени, то процент отказов в течение продолжительного периода времени является мерой безотказности продукции и может быть хорошей оценкой будущих затрат в гарантийный период. Но если параметр потока отказов продукции является не постоянным во времени (например, из-за ранних отказов), использование процента отказов за рассматриваемый период времени может ввести в заблуждение.
Если надежность продукции повышается, это не сразу повлияет на статистику, так как на нее будут влиять количество объектов с низкой надежностью, все еще находящихся на рынке. По этой причине рекомендуется использовать отдельную статистику для улучшенных объектов, например на основе номера, серии, типа, кода партии или даты изготовления.
С.4 Кривые M(t)
Если изменение параметра потока отказов во времени неизвестно, необходимо учитывать наработки отказавших объектов. Наработка может быть измерена в часах или днях (календарное время). Кривая M(t) в виде совокупного количества или процента отказов представляет собой функцию наработки, а не календарного времени как в С.3.
В некоторых случаях известно точное значение наработки, например при использовании счетчика времени или других счетчиков (например, одометр в автомобиле, счетчик копий в фотокопировальном устройстве и т.п.). В других случаях необходимо определить оценку наработки. Если наработка за день неизвестна, но может считаться приблизительно постоянной, для определения наработки могут использоваться дни вместо часов.
В соответствии с С.3 время (т.е. дату) постановки объектов на обслуживание можно определить на основе:
- даты поставки конечному пользователю;
- даты закупки/продажи;
- даты поставки дистрибьютору;
- даты изготовления.
Некоторые организации требуют, чтобы потребитель указал в регистрационной карте, когда оборудование было поставлено на обслуживание. В то же самое время используется карта потребителя для ремонта в гарантийный период (например, профилактическое обслуживание) и дальнейших действий маркетинга. Организация будет также иметь наименование и адрес потребителя в случае отзыва продукции. Однако не все потребители возвращают карту, так как возврат карты во многих странах не является обязательным условием для проведения гарантийного обслуживания.
В случае, когда продукция появляется в торговой сети с идентификационным кодом (например, мобильные телефоны), можно использовать время первого появления продукции в сети обслуживания.
Важно, чтобы одно и то же определение времени постановки продукции на обслуживание применялось ко всем объектам. Если есть различия, например, между рынками или каналами распределения продукции, рекомендуется применять отдельную статистику для каждого гомогенного набора данных.
Объекты, о которых известно, что они были изъяты из использования, должны быть включены в PAR только до момента времени (даты) изъятия их из использования. Таким образом, РАР оценивают для каждого периода времени. В случае, когда дистрибьютор обязан забирать изъятую продукцию, такие данные могут быть легко собраны.
Для отказавших объектов оценка времени (даты), когда они были поставлены на обслуживание и время (дата), когда объект отказал, могут быть определены. Наработку до отказа часто можно оценить (в порядке предпочтения) с помощью:
- наблюдаемого отказа;
- времени изъятия объекта из использования;
- времени отправки объекта на восстановление;
- времени получения объекта из ремонта.
Если известны эти данные, можно вычислить наработку до отказа. После возвращения объекта из ремонта может быть определено время, когда продукция будет снова поставлена на обслуживание, т.е. может быть включена в PAR. Для большого PAR (например, для потребительских товаров), когда время ремонта мало, а процент отказов низкий, временем ремонта можно пренебречь.
Календарное время проведения анализа отказов называют датой состояния. Для каждого объекта, учитываемого в PAR, наработку вычисляют как разность между временем, когда объект был поставлен на обслуживание, и датой состояния. Это можно легко выполнить с помощью компьютерной программы. В случаях, когда объект не имеет регистрационного номера (штрихового кода и т.п.), для формирования партии объектов, поставленных на обслуживание приблизительно в одно и то же время, можно использовать номера партии при изготовлении/продаже. В этом случае PAR вычисляют как функцию наработки, а не календарного времени как в С.3. Кривую M(t) строят в виде графика в соответствии с указаниями, приведенными в приложениях А и В.
Кривая отображает количество отказов как функцию наработки. Поэтому она не зависит от PAR и времени, когда объекты поступили на рынок, даже если параметр потока отказов является непостоянным. Для выявления периодов повышения надежности рекомендуется заново строить график кривой M(t) при внесении существенных изменений в продукцию или строить график кривой M(t) отдельно для каждого производственного года или квартала.
Кривую можно использовать для идентификации периодов постоянства параметра потока отказов и для его оценки. Кроме того, кривую можно использовать для идентификации ранних отказов, процента ранних отказов и особенностей ранних отказов. Кривую можно также использовать для идентификации периодов износа и оценки наработки до первого отказа и параметра потока отказов в период износа.
Форма кривой дает важную информацию для оценки ожидаемых затрат в течение гарантийного периода и управления повышением надежности. Выделяют три основных формы кривой.
Первая форма - прямая, проходящая через начало координат. Параметр потока отказов постоянен и его оценка равна угловому коэффициенту прямой.
Вторая форма - кривая, которая в начале координат возрастает, а затем выравнивается, приближаясь к прямой, пересекающей ось Y выше нуля (см. рисунок В.3). В этом случае имеются ранние отказы.
Третья форма - прямая линия, пересекающая ось Y ниже нуля. В этом случае имеется период времени без отказов (или период с незначительным количеством отказов) до наработки, соответствующей пересечению прямой с осью X. Так как кривые M(t) такой формы обычно соответствуют износу, наклон прямой (параметр потока отказов) обычно бывает высоким.
Рекомендуется строить график кривой M(t) для основных видов отказов или для отказов определенного компонента или модуля. Такой график может дать важную информацию для поиска неисправностей и подтверждения эффективности действий по улучшению.
С.5 Чувствительность к неопределенности данных
Во многих случаях данные о наработках и отказах известны с некоторой неопределенностью. Поэтому важно то, как эта неопределенность влияет на кривую M(t). Необходимо отметить, что эта неопределенность не имеет отношения к уровням доверия, рассчитываемым в соответствии с приложением В. Неопределенность данных влияет только на часть M(t) до той точки, с которой превращается в прямую линию. Поэтому оценки параметра потока отказов определяют на основе участка кривой M(t), представляющего собой прямую линию. Однако расстояние до точки, начиная с которой кривая превращается в прямую линию M(t), зависит от неопределенности данных. В общем случае неопределенность данных времени, когда продукция была предъявлена на обслуживание, переместит всю кривую M(t) вправо и изменит ее форму в соответствии с рисунком В.4. Поэтому оценка наработки до отказа для ранних отказов будет иметь более высокие значения из-за неопределенности данных. Чтобы избежать этого, организация должна предпринять усилия для получения как можно более точных исходных данных.
С.6 Как уменьшить неопределенность данных эксплуатации
Для нескольких больших систем потребитель и/или бригада, выполняющая ремонт, должны фиксировать данные о функционировании, отказах, техническом обслуживании и ремонте продукции в специальном журнале, который может быть электронным.
Для такой продукции, как потребительские товары, часто трудно получить точные данные со всех рынков. Поэтому изготовитель может выбрать один или несколько типичных рынков и предпринять усилия для получения точных данных эксплуатации, а данные с других рынков проанализировать более грубыми методами, например определить процент отказов в течение более длительного времени.
Если не весь ремонт выполняет изготовитель или его представитель, то изготовитель может заключить соглашение с одной или несколькими организациями по обслуживанию/ремонту для получения данных от них. Однако если определенная группа потребителей не обязана использовать конкретный пункт обслуживания/ремонта (например, через гарантийное соглашение), вычисление PAR становится очень трудной задачей.
Другой способ уменьшения неопределенности данных заключается в том, чтобы выбрать партию объектов (например, 1000 объектов), распределяемых через одного дистрибьютора таким способом, чтобы было известно, когда они были предъявлены на обслуживание. Кроме того, необходимо, чтобы эти объекты обслуживались в специальных пунктах обслуживания/ремонта, которые будут сообщать всю информацию об объектах партии.
В некоторых случаях данные, например наработка и коды отказа, могут быть зарегистрированы непосредственно на объекте и позже восстановлены. В некоторых случаях эти данные могут быть считаны дистанционно, например, у систем, связанных с компьютерными сетями.
Приложение D
(справочное)
Сведения о соответствии национальных стандартов
Российской Федерации ссылочным
международным стандартам
Таблица D.1
|
Обозначение ссылочного |
Обозначение и наименование соответствующего национального стандарта |
|
МЭК 60050-191:1990 |
* |
|
МЭК 61649:1997 |
ГОСТ Р 50779.27-2007 (МЭК 61649:1997) Статистические методы. Критерии согласия и доверительные интервалы для распределения Вейбулла |
|
МЭК 61710:2000 |
ГОСТ Р 50779.28-2007 (МЭК 61710:2000) Статистические методы. Степенная модель. Критерии согласия и методы оценки |
|
* Соответствующий национальный стандарт отсутствует. Поскольку языки МЭК 60050-191 включают в себя русский, рекомендуется непосредственное применение МЭК 60050-191. |
|
|
Ключевые слова: интенсивность отказов, параметр потока отказов, суммарная наработка, доверительный интервал, уровень значимости |