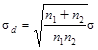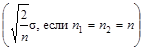ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО
ТЕХНИЧЕСКОМУ РЕГУЛИРОВАНИЮ И МЕТРОЛОГИИ
|
|
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ |
ГОСТ
Р (ИСО 3494:1976) |
Статистические методы
СТАТИСТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ДАННЫХ
Мощность тестов для средних и дисперсий
ISO
3494:1976
Statistical interpretation of data -
Power of tests relating to means and variances
(MOD)
![]()
Москва
Стандартинформ
2005
Предисловие
Цели и принципы стандартизации в Российской Федерации установлены Федеральным законом от 27 декабря 2002 г. № 184-ФЗ «О техническом регулировании», а правила применения национальных стандартов Российской Федерации - ГОСТ Р 1.0-2004 «Стандартизация в Российской Федерации. Основные положения»
Сведения о стандарте
1. ПОДГОТОВЛЕН Открытым акционерным обществом «Научно-исследовательский центр контроля и диагностики технических систем» (ОАО НИЦ КД) и Техническим комитетом по стандартизации ТК 125 «Статистические методы в управлении качеством продукции» на основе собственного аутентичного перевода стандарта, указанного в пункте 4
2. ВНЕСЕН Управлением развития, информационного обеспечения и аккредитации Федерального агентства по техническому регулированию и метрологии
3. УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 30 сентября 2005 г. № 235-ст
4. Настоящий стандарт является модифицированным по отношению к международному стандарту ИСО 3494:1976 «Статистическое представление данных - Мощность тестов для средних и дисперсий» (ISO 3494:1976 «Statistical interpretation of data - Power of tests relating to means and variances») путем изменения его структуры.
Наименование настоящего стандарта изменено относительно наименования указанного международного стандарта для приведения в соответствие с ГОСТ Р 1.5-2004 (подраздел 3.5).
Сопоставление структуры настоящего стандарта со структурой указанного международного стандарта приведено в дополнительном приложении А
5. ВВЕДЕН ВПЕРВЫЕ
Информация об изменениях к настоящему стандарту публикуется в ежегодно издаваемом информационном указателе «Национальные стандарты», а текст изменений и поправок - в ежемесячно издаваемых информационных указателях «Национальные стандарты». В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ежемесячно издаваемом информационном указателе «Национальные стандарты». Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте национального органа Российской Федерации по стандартизации в сети Интернет
СОДЕРЖАНИЕ
ГОСТ Р 50779.25-2005
(ИСО 3494:1976)
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
|
Статистические методы СТАТИСТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ДАННЫХ Мощность тестов для средних и дисперсий Statistical methods. Statistical interpretation of data. Power of tests relating to means and variances |
Дата введения - 2006-01-01
1. Область применения
Общие замечания
1) Настоящий стандарт согласован с ГОСТ Р 50779.21.
Настоящий стандарт применим, если распределение наблюдаемой случайной величины является нормальным в каждой совокупности. В ГОСТ Р 50779.21 упомянут только риск первого рода (или уровень значимости). Настоящий стандарт вводит понятия риска второго рода и мощности критерия.
2) Риск первого рода, обозначаемый a, является вероятностью отклонения нулевой гипотезы (проверяемой гипотезы), если эта гипотеза верна (случай двусторонних критериев), или максимальным значением этой вероятности (случай односторонних критериев). Неотклонение нулевой гипотезы приводит к принятию гипотезы, хотя не означает, что гипотеза верна.
Соответственно, риск второго рода, обозначаемый b - это вероятность неотклонения нулевой гипотезы, когда она является ложной. Дополнение вероятности ошибки второго рода - это мощность критерия (1 - b) (см. далее в «Исторических замечаниях»).
3) Поскольку значение риска первого рода выбирает потребитель в соответствии с последствиями (обычно используют значение a = 0,05 или a = 0,01), риск второго рода зависит от истинной гипотезы (нулевая гипотеза Н0 является ложной), т.е. альтернативной гипотезы. При сравнении среднего совокупности (далее - среднее) с заданным значением m0 конкретная альтернатива [которая была отклонена (m - m0 ≠ 0)] может соответствовать значению среднего совокупности m ≠ m0. Как правило, при сравнительных испытаниях средние и дисперсии альтернативы определены значениями параметра.
4) Кривая оперативной характеристики критерия показывает значение риска второго рода b как функцию параметра, определяющего альтернативу. Значение b зависит также от выбранного значения риска первого рода, объема выборки и типа критерия (двусторонний или односторонний).
При проверке гипотез о средних b также зависит от стандартного отклонения совокупности(ей). Если стандартное отклонение неизвестно, риск b не может быть известен точно.
5) Кривые оперативной характеристики позволяют решать следующие задачи:
a) задача 1: Для данной альтернативы и заданного объема выборки определить вероятность b неотклонения нулевой гипотезы (риск второго рода);
b) задача 2: Для данной альтернативы и заданного значения b определить объем выборки.
Хотя решить обе задачи позволяет единственный набор кривых, для облегчения практического использования приведены два набора кривых:
- наборы кривых 1.1 - 14.1, задающие риск b как функцию альтернативы для a = 0,05 или a = 0,01 и различных значений объема выборки;
- наборы кривых 1.2 - 14.2, задающие объем(ы) выборки как функцию альтернативы для a = 0,05 или a = 0,01 и различных значений риска b.
6) Необходимо обратить внимание на практическое значение представления статистик с помощью кривых. При проверке гипотезы вида m = m0 (или m1 = m2) желательно знать, можно ли сделать заключение с небольшим риском ошибки, что m ненамного отличается от m0 (или m1 не отличается от m2). Кроме того, выбор значения a = 0,05 или a = 0,01 для риска первого рода является достаточно произвольным. Поэтому полезно исследовать результаты процедуры проверки гипотез для значений, близких к m0 (или значения разности D = m1 - m2, близкие к 0), используя оба значения риска первого рода a = 0,05 и a = 0,01, и оценить посредством кривых оперативной характеристики значения риска b соответствующие различным альтернативам.
7) Наборы кривых с конкретными данными, приведенные в разделе 9, рассмотрены в разделах 3 - 8 настоящего стандарта в соответствии с ГОСТ Р 50779.21.
Исторические замечания
Понятия «риск первого рода» и «риск второго рода» ввели в 1928 г. Дж. Нейман и И.С. Пирсон, которые впоследствии пришли к заключению, что дополнение вероятности ошибки второго рода, названное ими «мощностью критерия» из-за способности показывать значимость альтернативы по отношению к нулевой гипотезе (проверяемая гипотеза), является более простым понятием. Эту «мощность» или вероятность обнаружения отклонения от нулевой гипотезы они обозначили символом b.
Не обязательно вводить термин «мощность». Можно рассматривать вероятность того, что проверка гипотез по выборке с уровнем значимости a показывает: параметр λ совокупности отличается (когда это действительно имеет место) не менее чем на указанное значение от заданного значения λ0, или их отношение меньше или равно заданному значению.
Символом b в ГОСТ Р 50779.10 обозначен риск второго рода, это же обозначение использовано и в настоящем стандарте.
2. Нормативные ссылки
В настоящем стандарте использованы нормативные ссылки на следующие стандарты:
ГОСТ Р 50779.10-2000 (ИСО 3534-1-93) Статистические методы. Вероятность и основы статистики. Термины и определения (ИСО 3534-1:1993 «Статистика. Словарь и условные обозначения. Часть 1. Вероятность и основные статистические термины», MOD)
ГОСТ Р 50779.21-2004 Статистические методы. Правила определения и методы расчета статистических характеристик по выборочным данным. Часть 1. Нормальное распределение (ИСО 2854:1976 «Статистическое представление данных. Методы оценки и проверки гипотез о средних и дисперсиях», NEQ)
Примечание - При пользовании настоящим стандартом целесообразно проверить действие ссылочных стандартов в информационной системе общего пользования - на официальном сайте национального органа Российской Федерации по стандартизации в сети Интернет или по ежегодно издаваемому информационному указателю «Национальные стандарты», который опубликован по состоянию на 1 января текущего года, и по соответствующим ежемесячно издаваемым информационным указателям, опубликованным в текущем году. Если ссылочный стандарт заменен (изменен), то при пользовании настоящим стандартом следует руководствоваться замененным (измененным) стандартом. Если ссылочный стандарт отменен без замены, то положение, в котором дана ссылка на него, применяется в части, не затрагивающей эту ссылку.
3. Сравнение среднего с заданным значением (дисперсия известна)
n - объем выборки.
m - среднее совокупности.
m0 - заданное значение среднего совокупности.
s - стандартное отклонение совокупности.
Для двустороннего критерия нулевая гипотеза: m = m0; альтернативная гипотеза: m ≠ m0.
Для одностороннего критерия нулевая гипотеза:
a) или m £ m0 с альтернативной гипотезой m > m0;
b) или m ³ m0 с альтернативной гипотезой m < m0.
3.3. Задача 1: n задан, необходимо определить риск b
Для различных значений m альтернатива определяется параметром λ (0 < λ < ∞):
a) ![]() для двустороннего критерия и
альтернативы m ≠ m0;
для двустороннего критерия и
альтернативы m ≠ m0;
b) ![]() для одностороннего критерия m £ m0 и
альтернативы m >
m0;
для одностороннего критерия m £ m0 и
альтернативы m >
m0;
c) ![]() для одностороннего критерия m ³ m0 и
альтернативы m <
m0.
для одностороннего критерия m ³ m0 и
альтернативы m <
m0.
Соответствующий набор кривых приведен на рисунках:
- 1.1 для двустороннего критерия и риска первого рода a = 0,05;
- 2.1 для двустороннего критерия и риска первого рода a = 0,01;
- 3.1 для одностороннего критерия и риска первого рода a = 0,05;
- 4.1 для одностороннего критерия и риска первого рода a = 0,01.
На этих рисунках b - ордината точки с абсциссой λ на кривой для ν = ∞.
3.4. Задача 2: значение b задано, необходимо определить объем выборки n
Для различных значений m альтернатива определяется параметром λ (0 < λ < ∞):
a) ![]() для двустороннего критерия и
альтернативы m ≠ m0;
для двустороннего критерия и
альтернативы m ≠ m0;
b) ![]() для одностороннего критерия m £ m0 и альтернативы m
> m0;
для одностороннего критерия m £ m0 и альтернативы m
> m0;
c) ![]() для одностороннего критерия m ³ m0 и
альтернативы m < m0.
для одностороннего критерия m ³ m0 и
альтернативы m < m0.
Соответствующий набор кривых приведен на рисунках:
- 1.2 для двустороннего критерия и риска первого рода a = 0,05;
- 2.2 для двустороннего критерия и риска первого рода a = 0,01;
- 3.2 для одностороннего критерия и риска первого рода a = 0,05;
- 4.2 для одностороннего критерия и риска первого рода a = 0,01.
На этих рисунках n - ордината точки с абсциссой λ на прямой линии (пунктирная линия), которая соответствует заданному значению b.
3.5. Пример - Производитель хлопковой пряжи гарантирует для каждой партии, которую он поставляет, что среднее разрывное усилие пряжи, выраженное в ньютонах, не менее m0 = 2,30. Потребитель согласен принимать партии, но желает проверить на образцах пряжи данной длины, взятых с различных бобин, что односторонний критерий в соответствии с ГОСТ Р 50779.21 не ведет к отклонению гипотезы m ³ m0 = 2,30 с риском первого рода a = 0,05 (здесь a - риск поставщика).
Потребителю известно, что среднее разрывных усилий различных партий может изменяться, но дисперсия разрывных усилий в партии является постоянной со стандартным отклонением s = 0,33.
3.5.1. Потребитель планирует выбирать по n = 10 бобин из партии и желает знать вероятность того, что он не будет отклонять гипотезу m ³ 2,30 (следовательно, будет принимать партию) при фактическом среднем разрывных усилий m = 2,10.
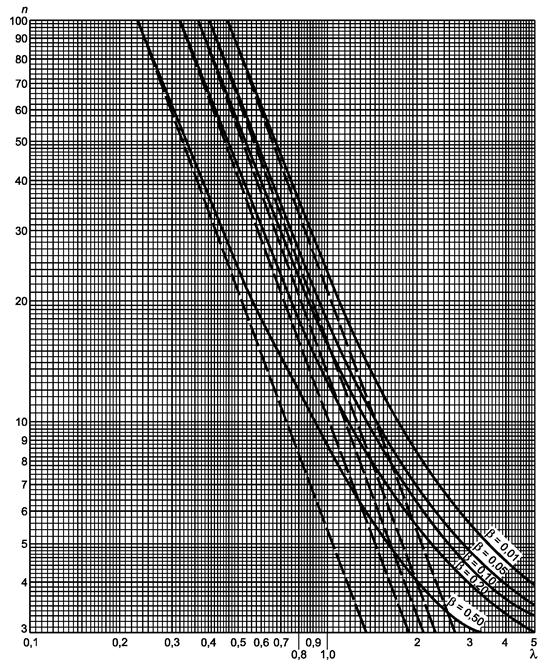
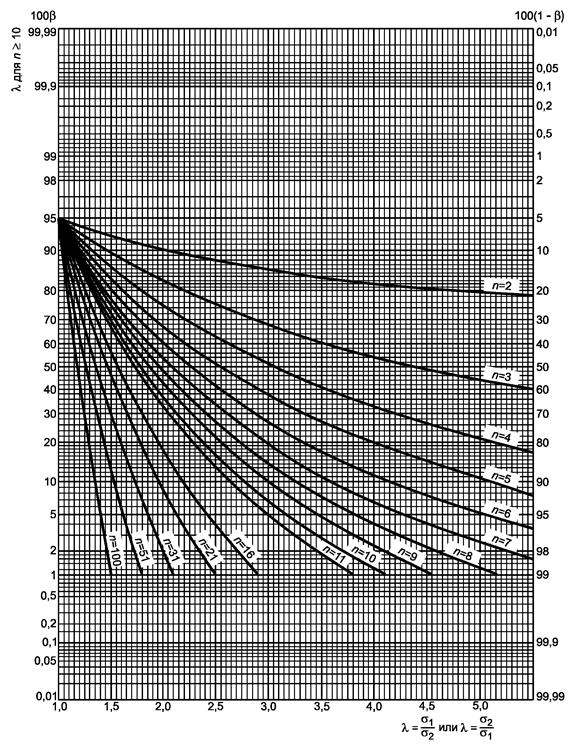
Набор кривых приведен на рисунке 3.1. Значение параметра λ для m = 2,10:
![]()
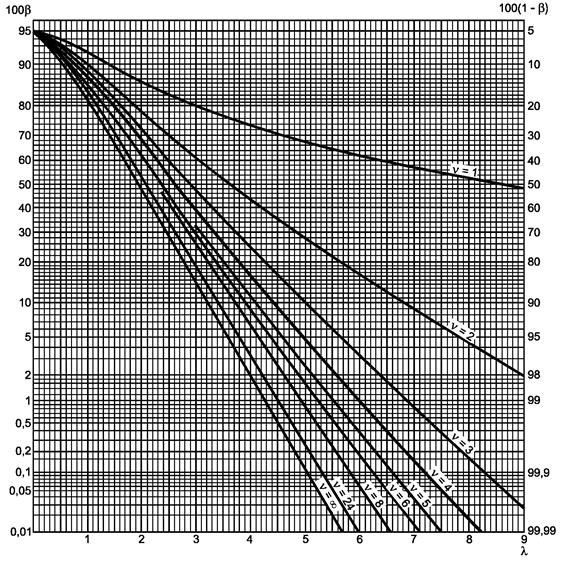
Прямая линия ν = ∞ дает для 100b значение 36, т.е. b = 0,36 или 36 %.
3.5.2. Это значение потребитель считает слишком высоким и решает отбирать выборку достаточного объема для того, чтобы уменьшить риск b до 0,10 (или 10 %), если m = 2,10.
Необходимый набор кривых приведен на рисунке 3.2. Значение параметра λ для m = 2,10:
![]()
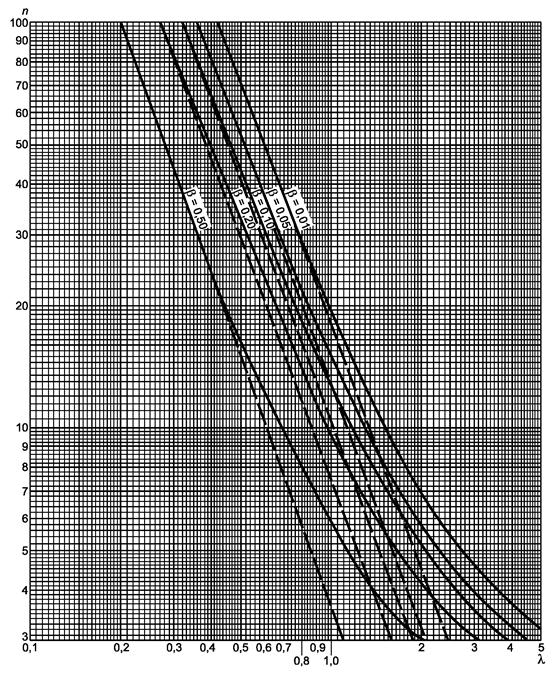
Значение n является ординатой точки с абсциссой λ = 0,61 на прямой линии (пунктирная линия), соответствующей b = 0,10, т.е. п = 22.
4. Сравнение среднего с заданным значением (дисперсия неизвестна)
Важное замечание
Риск второго рода b зависит от истинного значения s стандартного отклонения совокупности, которое является неизвестным. Следовательно, b может быть известно только приблизительно, хотя порядок s известен. При отсутствии любой предыдущей информации о значении s обычно используют оценку s, полученную по выборке.
Рекомендуется исследовать влияние стандартного отклонения на кривую оперативной характеристики. Погрешность может быть очень большой, если s оценивали по выборке небольшого объема. В этом случае рекомендуется выбирать s в пределах доверительных границ для s (см. ГОСТ Р 50779.21).
n - объем выборки.
m - среднее совокупности.
m0 - заданное значение среднего совокупности.
s - стандартное отклонение совокупности (вместо него будет использовано приближенное значение).
ν = n - 1.
Для двустороннего критерия нулевая гипотеза: m = m0; альтернативная гипотеза: m ≠ m0.
Для одностороннего критерия нулевая гипотеза:
a) или m £ m0 с альтернативной гипотезой m > m0;
b) или m ³ т0 с альтернативной гипотезой m < m0.
4.3. Задача 1: значение n задано, необходимо определить риск b
Для различных значений m альтернатива определяется параметром λ (0 < λ < ∞):
a) ![]() для двустороннего критерия и
альтернативы m ≠ m0;
для двустороннего критерия и
альтернативы m ≠ m0;
b) ![]() для одностороннего критерия m £ m0 и
альтернативы m > m0;
для одностороннего критерия m £ m0 и
альтернативы m > m0;
c) ![]() для одностороннего критерия m ³ m0 и
альтернативы m < m0.
для одностороннего критерия m ³ m0 и
альтернативы m < m0.
Соответствующий набор кривых приведен на рисунках:
- 1.1 для двустороннего критерия и риска первого рода a = 0,05;
- 2.1 для двустороннего критерия и риска первого рода a = 0,01;
- 3.1 для одностороннего критерия и риска первого рода a = 0,05;
- 4.1 для одностороннего критерия и риска первого рода a = 0,01.
На этих рисунках b - ордината точки с абсциссой λ на кривой для ν = n - 1.
4.4. Задача 2: значение b задано, необходимо определить объем выборки n
Для различных значений m альтернатива определяется параметром λ (0 < λ < ∞):
a) ![]() для двустороннего критерия и
альтернативы m ≠ m0;
для двустороннего критерия и
альтернативы m ≠ m0;
b) ![]() для одностороннего критерия m £ m0 и
альтернативы m > m0;
для одностороннего критерия m £ m0 и
альтернативы m > m0;
c) ![]() для одностороннего критерия m ³ m0 и
альтернативы m < m0.
для одностороннего критерия m ³ m0 и
альтернативы m < m0.
Соответствующий набор кривых приведен на рисунках:
- 1.2 для двустороннего критерия и риска первого рода a = 0,05;
- 2.2 для двустороннего критерия и риска первого рода a = 0,01;
- 3.2 для одностороннего критерия и риска первого рода a = 0,05;
- 4.2 для одностороннего критерия и риска первого рода a = 0,01.
На этих рисунках n - ордината точки с абсциссой λ на кривой, которая соответствует заданному значению b.
4.5. Пример - В условиях примера 3.5 потребитель не знает точное значение стандартного отклонения разрывного усилия пряжи. Однако он знает, что s почти наверняка лежит в следующих границах:
s1 = 0,30; ss = 0,45.
4.5.1. Потребитель хотел бы отбирать по n = 10 бобин из партии и желает знать вероятность того, что он не будет отклонять гипотезу т ³ 2,30 (следовательно, будет принимать партию), когда фактическое среднее разрывное усилие составляет т = 2,101).
1) Вероятность того, что при использовании критерия Стьюдента с уровнем значимости a = 0,05 значение m = 2,10 не будет обнаружено как значение m менее m0 = 2,30.
Набор соответствующих кривых приведен на рисунке 3.1. Значения параметра λ, которые соответствуют критическим значениям s:
![]()
![]()
Соответствующие значения 100b, найденные с помощью интерполяции, для ν = 9:
b1 = 0,40 (или 40 %);
b2 = 0,64 (или 64 %).
4.5.2. Потребитель желает, чтобы в самой неблагоприятной ситуации (s = ss = 0,45), риск b не превышал 0,10 (или 10 %), если m = 2,10.
Набор кривых приведен на рисунке 3.2.
![]()
Легко определить, что для b = 0,10 и λ = 0,44: n = 45.
Если после контроля нескольких партий выявлено, что стандартное отклонение постоянно и s можно оценить с большей точностью, объем выборки, который будет использован для следующих партий, может быть уменьшен с гарантиями производителя и соответствующим обслуживанием потребителя.
5. Сравнение двух средних (дисперсия известна)
|
Характеристика |
Совокупность № 1 |
Совокупность № 2 |
|
Объем выборки |
n1 |
n2 |
|
Среднее |
m1 |
m2 |
|
Дисперсия |
|
|
|
Стандартное отклонение разности средних двух выборок |
|
|
Для двустороннего критерия нулевая гипотеза: m1 = m2; альтернативные гипотезы: m1 ≠ m2.
Для одностороннего критерия нулевая гипотеза:
a) или m1 £ m2 с альтернативной гипотезой m1 > m2;
b) или m1 ³ m2 с альтернативной гипотезой m1 < m2.
5.3. Задача 1: n1 и n2 заданы, необходимо определить риск b
Для различных значений разности m1 - m2 альтернатива определяется параметром λ (0 < λ < ∞):
a) ![]() для двустороннего критерия и
альтернативы m1 ≠ m2;
для двустороннего критерия и
альтернативы m1 ≠ m2;
b) ![]() для одностороннего критерия m1 £ m2 и
альтернативы m1
> m2;
для одностороннего критерия m1 £ m2 и
альтернативы m1
> m2;
c) ![]() для одностороннего критерия m1 ³ m2 и
альтернативы m1
< m2.
для одностороннего критерия m1 ³ m2 и
альтернативы m1
< m2.
Соответствующий набор кривых приведен на рисунках:
- 1.1 для двустороннего критерия и риска первого рода a = 0,05;
- 2.1 для двустороннего критерия и риска первого рода a = 0,01;
- 3.1 для одностороннего критерия и риска первого рода a = 0,05;
- 4.1 для одностороннего критерия и риска первого рода a = 0,01.
На этих рисунках b - ордината точки с абсциссой λ на кривой для ν = ∞.
Если общий объем двух выборок фиксирован n1 + n2 = 2n, наилучшая эффективность (минимальное значение b) достигается, когда
![]()
следовательно,
![]()
![]()
![]()
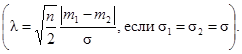
5.4. Задача 2: значение b задано, необходимо определить объемы выборок n1 и n2
Используя на рисунках 1.1, 2.1, 3.1 или 4.1 кривую, обозначенную ν = ∞, можно решить задачу в общем случае. Точка с ординатой b на этой кривой имеет абсциссу λ. Для решения задачи подходит любая пара (n1, n2), удовлетворяющая условию
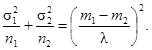
Для самой экономичной выборки, когда сумма n1 + n2 минимальна, справедливо условие
![]()
следовательно,
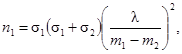
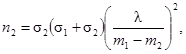
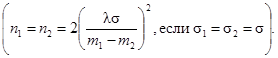
В частном случае, когда s1 = s2 = s; n1 = n2 = n, удобно для различных значений разности m1 - m2 определять альтернативу с помощью параметра λ (0 < λ < ∞):
a) ![]() для двустороннего критерия и
альтернативы m1 ≠ m2;
для двустороннего критерия и
альтернативы m1 ≠ m2;
b) ![]() для одностороннего критерия m1 £ m2 и
альтернативы m1
> m2;
для одностороннего критерия m1 £ m2 и
альтернативы m1
> m2;
c) ![]() для одностороннего критерия m1 ³ m2 и
альтернативы m1
< m2.
для одностороннего критерия m1 ³ m2 и
альтернативы m1
< m2.
Соответствующий набор кривых приведен на рисунках:
- 1.2 для двустороннего критерия и риска первого рода a = 0,05;
- 2.2 для двустороннего критерия и риска первого рода a = 0,01;
- 3.2 для одностороннего критерия и риска первого рода a = 0,05;
- 4.2 для одностороннего критерия и риска первого рода a = 0,01.
Значение n является ординатой точки с абсциссой λ на прямой линии (пунктирная линия), соответствующей заданному значению b.
5.5. Пример - Изготовитель хлопковой пряжи изменил производственный процесс, но согласно его заявлению, среднее разрывных усилий не изменилось: (m1 = m2), m1 соответствует старому процессу, а m2 - новому.
Потребитель готов принять новый процесс, но желает проверить заявление производителя; для этого он отбирает образцы пряжи заданной длины из различных бобин для проверки гипотезы m1 = m2 в соответствии с ГОСТ Р 50779.21 с риском первого рода a = 0,05 (a является здесь риском изготовителя).
Потребитель знает, что для всей продукции этого производителя дисперсия разрывных усилий является практически постоянной и характеризуется стандартным отклонением s = 0,33.
5.5.1. Потребитель планирует выбирать по 10 бобин из партии каждого из двух процессов и желает определить значение вероятности того, что гипотеза m1 = m2 не будет отклонена (следовательно, будет принята партия нового процесса), в то время как фактически разность |m1 - m2| равна 0,30.
Соответствующий набор кривых приведен на рисунке 1.1, где
![]()
|m1 - m2| = 0,30,
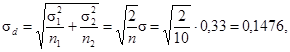
![]()
Кривая, обозначенная ν = ∞, дает для 100b значение 47. Таким образом, b = 0,47 или 47 %.
5.5.2. Это значение потребитель считает слишком высоким, он решает отобрать выборки такого большого объема, чтобы уменьшить риск b до 0,10 (или 10 %) при |m1 - m2| = 0,30.
Соответствующий набор кривых приведен на рисунке 1.2, где
![]()
Значение n, определенное с помощью прямой линии (пунктирная линия) для b = 0,10: n = 26.
6. Сравнение двух средних (дисперсии неизвестны и равны)
Важное замечание
Риск второго рода b зависит от истинного значения стандартного отклонения двух совокупностей, которое является неизвестным. Следовательно, b может быть известно только приблизительно, однако порядок s может быть известен. В отсутствие какой-либо предварительной информации обычно в качестве s используют оценку s, полученную по выборке.
Настоятельно рекомендуется исследовать влияние стандартного отклонения s на значения, определяемые по кривым ошибок. В тех случаях, когда s оценивали по выборке небольшого объема, погрешность может быть очень большой. В этом случае рекомендуется использовать s в пределах доверительных границ для s, определенных в соответствии с ГОСТ Р 50779.21.
|
Характеристика |
Совокупность № 1 |
Совокупность № 2 |
|
Объем выборки |
n1 |
n2 |
|
Среднее |
m1 |
m2 |
|
Дисперсия, которая будет заменена приближенным значением |
s2 |
s2 |
|
Число степеней свободы |
ν = п1 + п2 - 2 (2 · (n - 1), если п1 = n2 = n) |
|
|
Стандартное отклонение разности средних двух выборок |
|
|
Для двустороннего критерия нулевая гипотеза: m1 = m2; альтернативная гипотеза: m1 ≠ m2.
Для одностороннего критерия нулевая гипотеза:
a) или m1 £ m2 с альтернативной гипотезой m1 > m2;
b) или m1 ³ m2 с альтернативной гипотезой m1 < m2.
6.3. Задача 1: значения n1 и n2 заданы, необходимо определить риск b
Для различных значений разности m1 - m2 альтернатива определяется параметром λ (0 < λ < ∞):
a) ![]() для двустороннего критерия с
альтернативой m1 ≠ m2;
для двустороннего критерия с
альтернативой m1 ≠ m2;
b) ![]() для одностороннего критерия m1 £ m2 с
альтернативой m1
> m2;
для одностороннего критерия m1 £ m2 с
альтернативой m1
> m2;
c) ![]() для одностороннего критерия m1 ³ m2 с
альтернативой m1
< m2.
для одностороннего критерия m1 ³ m2 с
альтернативой m1
< m2.
Соответствующий набор кривых приведен на рисунках:
- 1.1 для двустороннего критерия и риска первого рода a = 0,05;
- 2.1 для двустороннего критерия и риска первого рода a = 0,01;
- 3.1 для одностороннего критерия и риска первого рода a = 0,05;
- 4.1 для одностороннего критерия и риска первого рода a = 0,01.
На этих рисунках b - ордината точки с абсциссой λ на кривой для ν = n1 + n2 - 2.
Если общий объем двух выборок фиксирован n1 + n2 = 2n, представляет интерес случай n1 = n2 = n, когда b минимально. Тогда
![]()
6.4. Задача 2: значение b задано, необходимо определить общий объем выборок n
Для различных значений разности m1 - m2 альтернатива определяется параметром λ (0 < λ < ∞):
a) ![]() для двустороннего критерия с
альтернативой m1 ≠ m2;
для двустороннего критерия с
альтернативой m1 ≠ m2;
b) ![]() для одностороннего критерия m1 £ m2 с
альтернативой m1
> m2;
для одностороннего критерия m1 £ m2 с
альтернативой m1
> m2;
c) ![]() для одностороннего критерия m1 ³ m2 с
альтернативой m1
< m2.
для одностороннего критерия m1 ³ m2 с
альтернативой m1
< m2.
Соответствующий набор кривых приведен на рисунках:
- 1.2 для двустороннего критерия и риска первого рода a = 0,05;
- 2.2 для двустороннего критерия и риска первого рода a = 0,01;
- 3.2 для одностороннего критерия и риска первого рода a = 0,05;
- 4.2 для одностороннего критерия и риска первого рода a = 0,01.
На этих рисунках n является ординатой точки с абсциссой λ на кривой, соответствующей заданному значению b.
6.5. Пример - Тот же, что и в 5.5, но потребитель не знает точного значения стандартного отклонения разрывных усилий. Он только знает с большой вероятностью, что для этих двух партий s1 = s2.
6.5.1. Потребитель предполагает выбирать по 10 бобин из партии каждого из двух процессов и желает знать вероятность того, что он не будет отклонять гипотезу m1 = m2 (следовательно, будет принимать партию нового процесса), когда фактически |т1 - т2| = 0,301).
1) Вероятность того, что при использовании критерия Стьюдента с уровнем значимости a = 0,05 разность ׀m1 - m2׀ = 0,30 не будет различима.
Измерения, выполненные на двух выборках, дают следующие результаты:
a) первая партия: ![]()
b)
вторая партия: ![]()
Небольшое различие между суммами квадратов хорошо согласуется с гипотезой s21 = s22 (см. ГОСТ Р 50779.21).
Оценка дисперсии s2 для этих партий:
![]()
Верхняя граница s2 с уровнем доверия (1 - a) = 0,95 (см. ГОСТ Р 50779.21):
![]()
Поэтому маловероятно, что s превысит значение
![]()
Соответствующий набор кривых приведен на рисунке 1.1 для
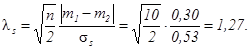
Для ν = 18 легко определить с помощью интерполяции, что соответствующее значение 100b близко к 80, т.е. верхний предел значения риска второго рода приблизительно равен 0,80 (или 80 %).
6.5.2. Потребитель желает, чтобы при самой неблагоприятной гипотезе (s = ss = 0,53) значение b не превосходило 0,20 (или 20 %), когда m1 - m2 = 0,30.
Соответствующий набор кривых приведен на рисунке 1.2, кривая b = 0,20
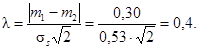
Для b = 0,20 и λ = 0,4: n = 49.
Ста результатов измерений (2 · 50 = 100) хватает, чтобы получить довольно точную оценку s, на основе которой набор кривых, приведенный на рисунке 1.1, позволяет получить приближенное значение риска второго рода, соответствующего альтернативе m1 - m2 = 0,30.
7. Сравнение дисперсии или стандартного отклонения с заданным значением
n - объем выборки.
s2 - дисперсия совокупности (s - стандартное отклонение совокупности);
s02 - заданное значение дисперсии (s0 - заданное значение стандартного отклонения).
Для двустороннего критерия нулевая гипотеза: s2 = s02 (s = s0); альтернативная гипотеза: s2 ≠ s02 (s ≠ s0).
Для одностороннего критерия нулевая гипотеза:
a) или s2 £ s02 (s £ s0) с альтернативной гипотезой s 2 > s02 (s > s0);
b) или s2 ³ s02 (s ³ s0) с альтернативной гипотезой s2 < s02 (s < s0).
Во всех случаях альтернатива определяется параметром
λ = s/s0:
0 < λ < ∞ для двустороннего критерия;
1 < λ < ∞ для одностороннего критерия s2 £ s02 (s £ s0);
0 < λ < 1 для одностороннего критерия s2 ³ s02 (s ³ s0).
7.3. Задача 1: значение n задано, необходимо определить риск b
Соответствующий набор кривых приведен на рисунках:
- 5.1 для двустороннего критерия и риска первого рода a = 0,05;
- 6.1 для двустороннего критерия и риска первого рода a = 0,01;
- 7.1 для одностороннего критерия s2 £ s02 и риска первого рода a = 0,05;
- 8.1 для одностороннего критерия s2 £ s02 и риска первого рода a = 0,01;
- 9.1 для одностороннего критерия s2 ³ s02 и риска первого рода a = 0,05;
- 10.1 для одностороннего критерия s2 ³ s02 и риска первого рода a = 0,01.
На этих рисунках b - ордината точки с абсциссой λ на кривой для соответствующего n.
7.4. Задача 2: значение b задано, необходимо определить объем выборки n
Соответствующий набор кривых приведен на рисунках:
- 5.2 для двустороннего критерия и риска первого рода a = 0,05;
- 6.2 для двустороннего критерия и риска первого рода a = 0,01;
- 7.2 для одностороннего критерия s2 < s02 и риска первого рода a = 0,05;
- 8.2 для одностороннего критерия s2 < s02 и риска первого рода a = 001;
- 9.2 для одностороннего критерия s2 > s02 и риска первого рода a = 0,05;
- 10.2 для одностороннего критерия s2 > s02 и риска первого рода a = 0,01.
На этих рисунках n - ордината точки с абсциссой λ на кривой, соответствующей заданному значению b.
7.5. Пример - Производитель хлопковой пряжи заявляет, что он улучшил качество процесса изготовления пряжи, в результате чего дисперсия разрывных усилий, которая ранее характеризовалась стандартным отклонением s0 = 0,45 (s02 = 0,2025), уменьшилась.
Потребитель готов больше заплатить за продукцию улучшенного качества при условии, что это действительно так, и допускает лишь маленький риск обнаружения улучшения при его отсутствии. Он решает применить односторонний критерий s2 ³ s02 = 0,2025 (s ³ 0,45) для риска первого рода a = 0,05 (здесь a - риск потребителя).
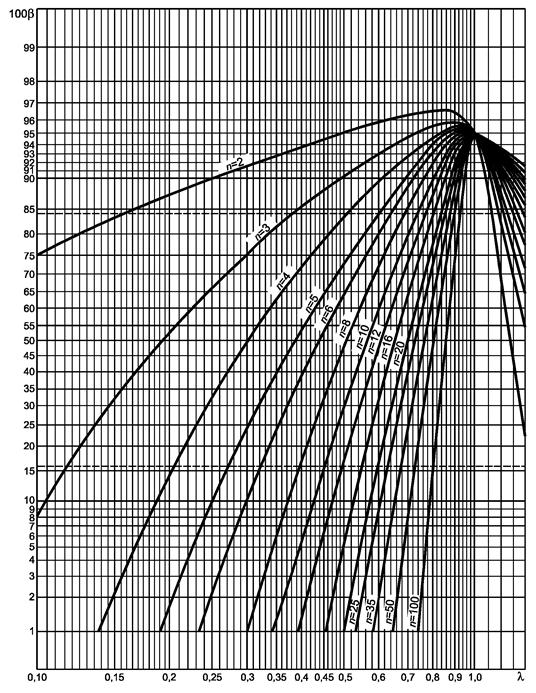
7.5.1. Потребитель предлагает отобрать по n = 12 бобин от партии нового процесса и желает знать значение вероятности того, что он не будет отклонять гипотезу s > 0,45 (следовательно, не обнаружит улучшения), в то время как стандартное отклонение уменьшилось до значения s = 0,30.
Соответствующий набор кривых приведен на рисунке 9.1 для
![]()
Кривая n = 12 дает для 100b приближенное значение 51, т.е. b = 0,51 или 51 %.
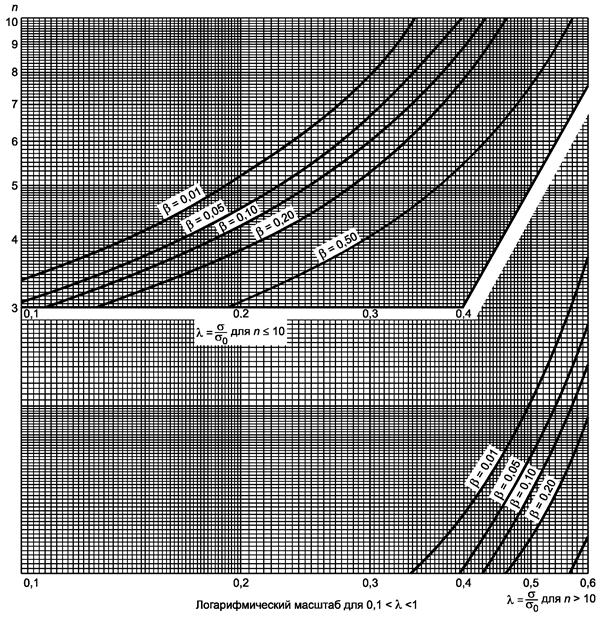
7.5.2. Потребитель определяет, что он имеет высокий риск необнаружения улучшения. Поэтому он решает выбрать достаточно большой объем выборки, а значение b уменьшить до 0,10 (или 10 %) для s = 0,30.
Соответствующий набор кривых приведен на рисунке 9.2.
Для b = 0,10 и λ = 0,67: n = 29.
8. Сравнение двух дисперсий или двух стандартных отклонений
Кривые оперативных характеристик приведены только для случая, когда рассмотрены две выборки одного объема.
Дисперсия совокупности № 1: s12 (стандартное отклонение s1).
Дисперсия совокупности № 2: s22 (стандартное отклонение s2).
Объем выборки № 1: n1 = n.
Объем выборки № 2: n2 = n.
Для двустороннего критерия нулевая гипотеза: s12 = s22 (s1 = s2); альтернативная гипотеза: s12 ≠ s22 (s1 ≠ s2). Они определяются значением параметра λ:
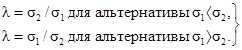 (1
< λ < ∞).
(1
< λ < ∞).
Для одностороннего критерия нулевая гипотеза:
a) или s12 £ s22 (s1 < s2) с альтернативной гипотезой s12 > s22 (s1 > s2) и параметром λ = s1/s2 (1 < λ < ∞);
b) или s12 ³ s22 (s1 > s2) с альтернативной гипотезой s12 £ s22 (s1 < s2) и параметром λ = s2/s1 (1 < λ < ∞).
8.3. Задача 1: значение n задано, необходимо определить риск b
Соответствующий набор кривых приведен на рисунках:
- 11.1 для двустороннего критерия и риска первого рода a = 0,05;
- 12.1 для двустороннего критерия и риска первого рода a = 0,01;
- 13.1 для одностороннего критерия и риска первого рода a = 0,05;
- 14.1 для одностороннего критерия и риска первого рода a = 0,01.
На этих рисунках b - ордината точки с абсциссой λ на кривой для соответствующего n.
8.4. Задача 2: значение b задано, необходимо определить объем n
Соответствующий набор кривых приведен на рисунках:
- 11.2 для двустороннего критерия и риска первого рода a = 0,05;
- 12.2 для двустороннего критерия и риска первого рода a = 0,01;
- 13.2 для одностороннего критерия и риска первого рода a = 0,05;
- 14.2 для одностороннего критерия и риска первого рода a = 0,01.
На этих рисунках n - ордината точки с абсциссой λ на кривой, соответствующей заданному значению b.
8.5. Пример - Производитель предлагает потребителю две партии хлопковой пряжи. Цена партии номер один немного выше, поскольку ей соответствует меньшая дисперсия разрывных усилий.
Потребитель готов выбрать партию номер один, если дисперсия действительно меньше и допускает маленький риск обнаружения, что s1 < s2, в то время как фактически s1 ³ s2. Он решает применить односторонний критерий s12 ³ s22 (s1 ³ s2) в соответствии с ГОСТ Р 50779.21 с риском первого рода a = 0,05 (здесь a - риск потребителя).
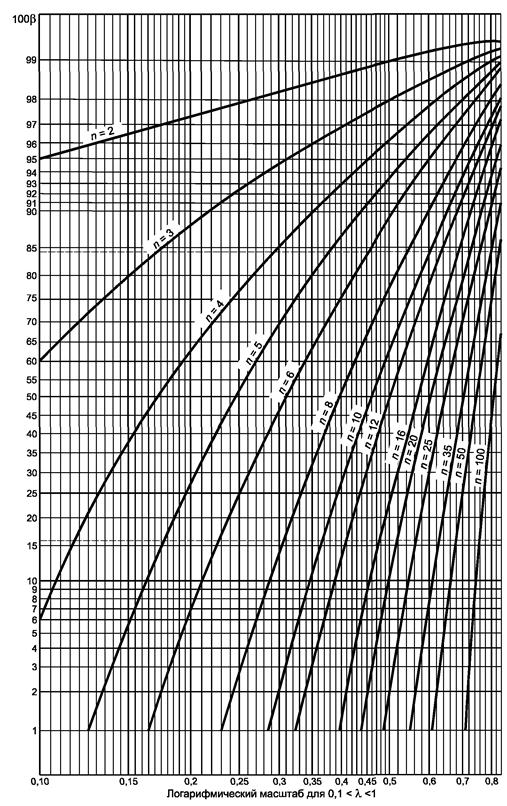
8.5.1. Потребитель предполагает отбирать по n = 20 бобин от каждой партии и желает определить вероятность того, что он не будет отклонять гипотезу s1 ³ s2 (следовательно, не обнаружит, что партия номер один имеет меньшую дисперсию, чем партия номер два), в то время как s1 = 2/3s2.
Соответствующий набор кривых приведен на рисунке 13.1:
![]()
Для n = 20 соответствующее значение 100b близко к 48, т.е. b = 0,48 или 48 %.
8.5.2. Потребитель определяет, что риск необнаружения усовершенствования слишком высок. Поэтому он решает отбирать из каждой партии большую выборку, чтобы значение b уменьшить до 0,10 (или 10 %), когда s1/s2 = 2/3.
Соответствующий набор кривых приведен на рисунке 13.2.
Для b = 0,10 и λ = 1,5: n = 55.
9. Наборы кривых
Таблица 1 - Перечень наборов кривых
|
Номер раздела |
Гипотеза |
Риск первого рода |
Номер рисунка с набором кривых |
|
|
Задача 11) |
Задача 22) |
|||
|
Сравнение средних |
||||
|
3 |
m = m0: известно |
0,05 |
||
|
4 |
m = m0: неизвестно |
|||
|
5 |
m1 = m2: s1, s2 известны |
0,01 |
||
|
6 |
m1 = m2: s1 = s2 неизвестно |
|||
|
3 |
m £ m0, m ³ m0: s известно |
0,05 |
||
|
4 |
m £ m0, m ³ m0: s неизвестно |
|||
|
5 |
m1 £ m2, m1 ³ m2: s1, s2 известны |
0,01 |
||
|
6 |
m1 £ m2, m1 ³ m2: s1 = s2 неизвестно |
|||
|
7 |
Сравнение дисперсии или стандартного отклонения с заданным значением |
|||
|
s2 = s02 |
0,05 |
|||
|
0,01 |
||||
|
s2 £ s02 |
0,05 |
|||
|
0,01 |
||||
|
s2 ³ s02 |
0,05 |
|||
|
0,01 |
||||
|
8 |
Сравнение двух дисперсий или двух стандартных отклонений |
|||
|
s12 = s22 |
0,05 |
|||
|
0,01 |
||||
|
s12 £ s22; s12 ³ s22 |
0,05 |
|||
|
0,01 |
||||
|
1) Объем выборки задан, необходимо определить b. 2) b задан, необходимо определить объем выборки. |
||||
Таблица 2 - Перечень рисунков с набором кривых
|
Номер рисунка с набором кривых |
Масштаб |
|
|
Абсцисса |
Ордината |
|
|
Линейный |
Нормальный |
|
|
Линейный |
Логарифмический |
|
|
Логарифмический |
Нормальный |
|
|
Логарифмический |
Логарифмический |
|
|
Логарифмический для λ < 1 |
Нормальный |
|
|
Линейный для λ > 1 |
Нормальный |
|
|
Логарифмический для λ < 1 |
Логарифмический |
|
|
Линейный для λ > 1 |
Логарифмический |
|
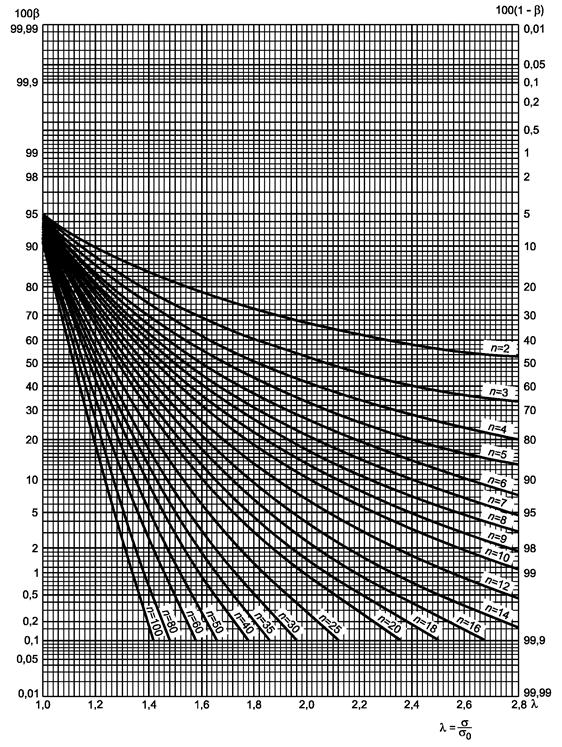
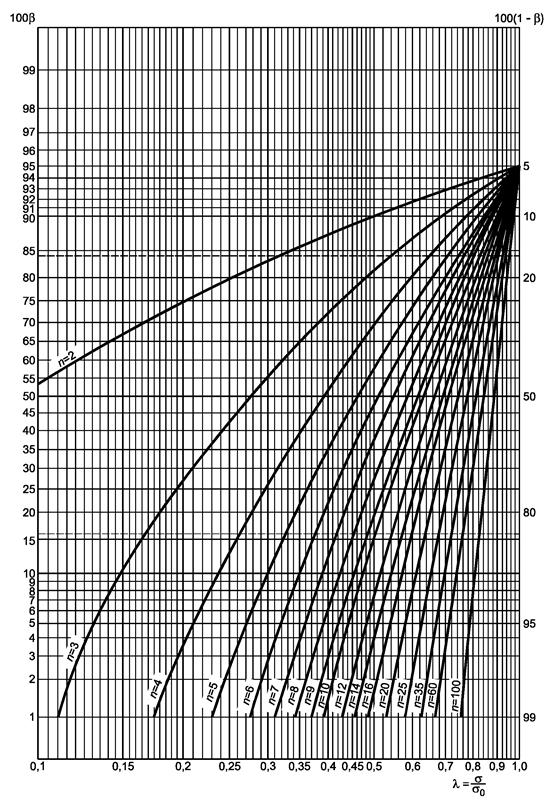
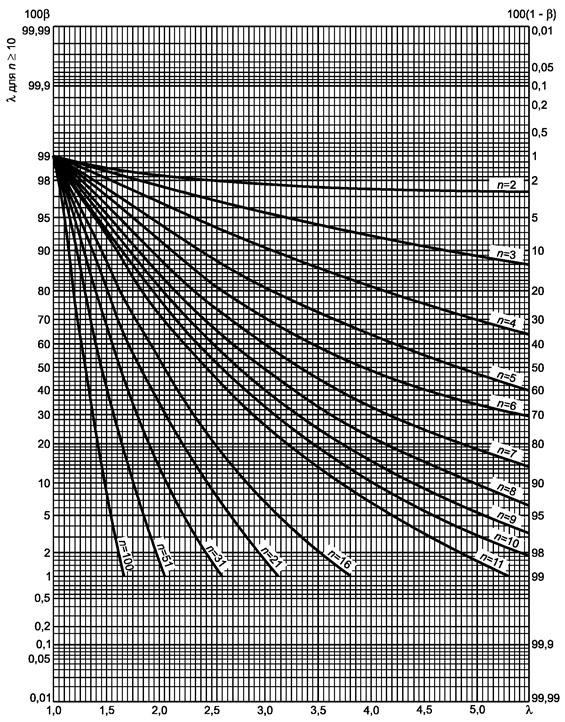
Рисунок 1.1 - Двусторонний критерий сравнения средних (риск первого рода a = 0,05)
a) Гипотеза m = m0:
- если
s
известно, используют кривую ν = ∞ с ![]()
- если
s
неизвестно, используют кривую ν = n - 1 с ![]()
![]()
b) Гипотеза m1 = m2:
-
если s1 и s2
известны, используют кривую ν = ∞ с 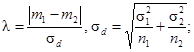
- если s1 и s2 неизвестны, используют кривую ν = n1 + n2 - 2
с 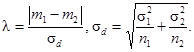
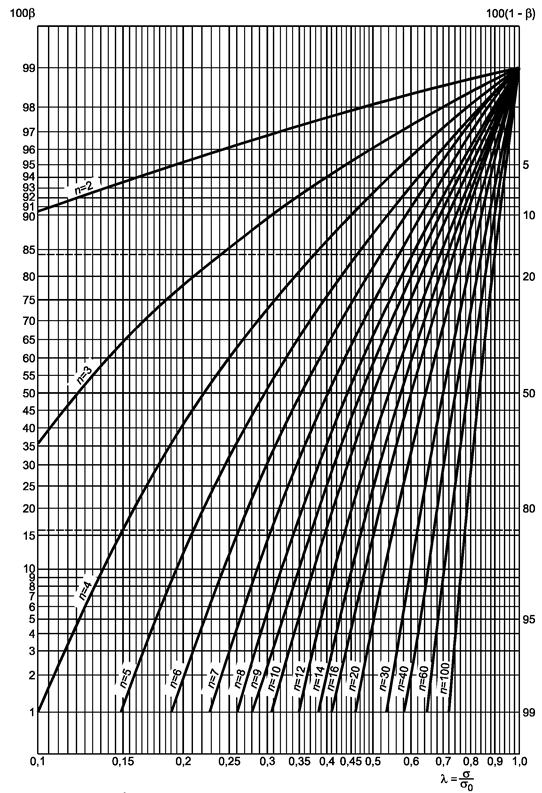
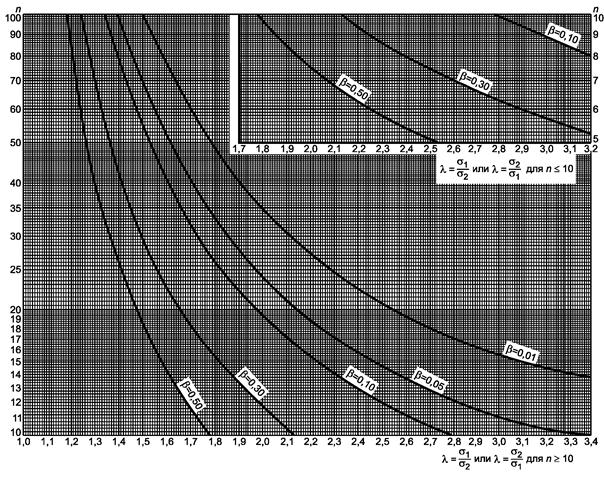
Рисунок 1.2 - Двусторонний критерий сравнения средних (риск первого рода a = 0,05)
a) Гипотеза m = m0:
- если
s
известно, используют прямые прерывистые линии с ![]()
- если
s
неизвестно, используют кривые с ![]()
b) Гипотеза m1 = m2
- если
s1 = s2 = s
известно, используют прямые прерывистые линии с ![]()
-
если s1 = s2 = s
неизвестно, используют кривые с ![]()
n1 = n2 = n (общий объем двух выборок).
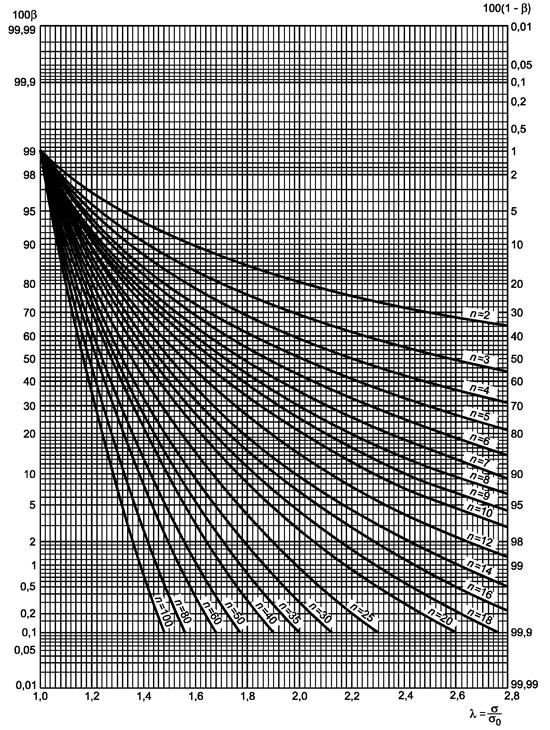
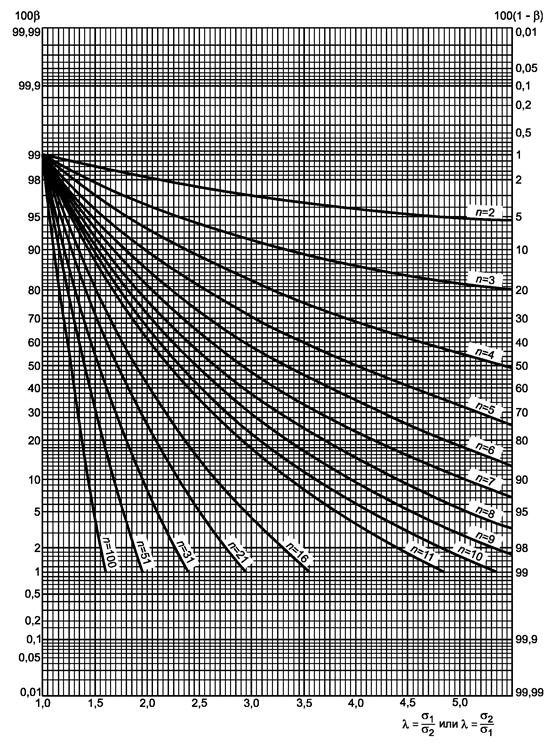
Рисунок 2.1 - Двусторонний критерий сравнения средних (риск первого рода a = 0,01)
a) Гипотеза m = m0:
-
если s
известно, используют кривую ν = ∞ с ![]()
-
если s
неизвестно, используют кривую ν = п - 1 с ![]()
b) Гипотеза m1 = m2:
-
если s1 и s2
известны, используют кривую ν = ∞ с 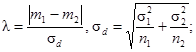
- если s1 и s2 неизвестны, используют кривую ν = n1 + n2 - 2
с 
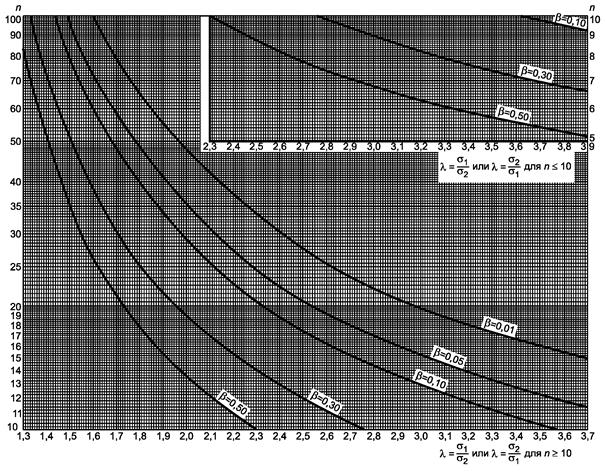
Рисунок 2.2 - Двусторонний критерий сравнения средних (риск первого рода a = 0,01)
a) Гипотеза m = m0:
-
если s
известно, используют прямые прерывистые линии с ![]()
-
если s
неизвестно, используют кривые с ![]()
b) Гипотеза m1 = m2:
-
если s1 = s2 = s
известно, используют прямые прерывистые линии с ![]()
-
если s1 = s2 = s
неизвестно, используют кривые с ![]()
n1 = n2 = n (общий объем двух выборок).
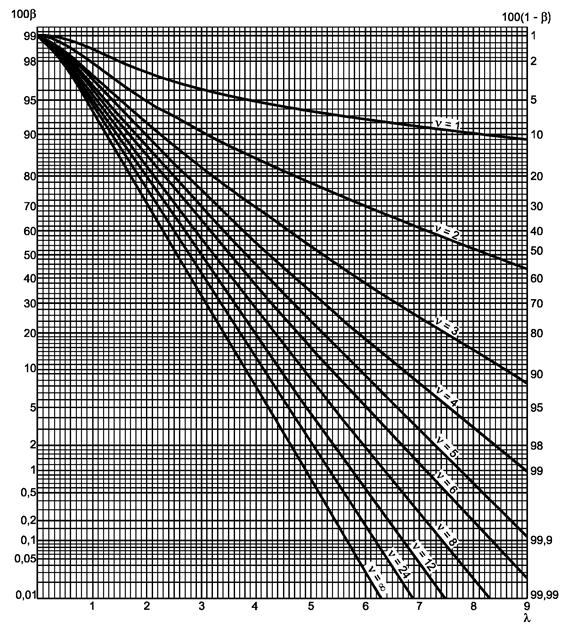
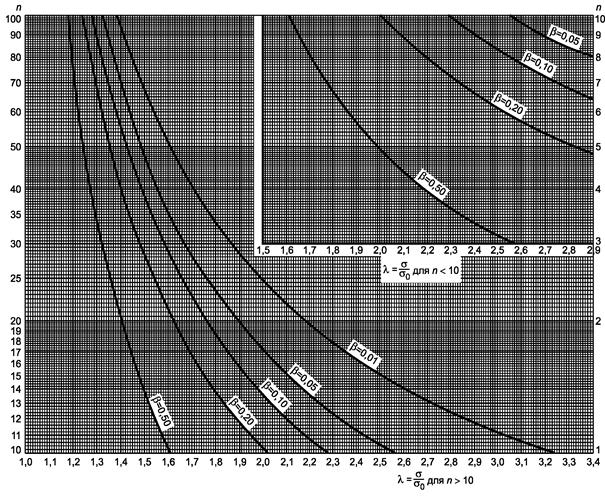
Рисунок 3.1 - Односторонний критерий сравнения средних (риск первого рода a = 0,05)
a) Гипотеза m £ m0 или m ³ m0:
-
если s
известно, используют кривую ν = ∞ с ![]()
-
если s
неизвестно, используют кривую ν = п - 1 с ![]()
b) Гипотеза m1 £ m2 или m1 ³ m2:
-
если s1 и s2
известны, используют кривую ν = ∞ с 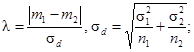
-
если s1 и s2
неизвестны, используют кривую ν = n1 + n2 - 2
с 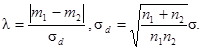
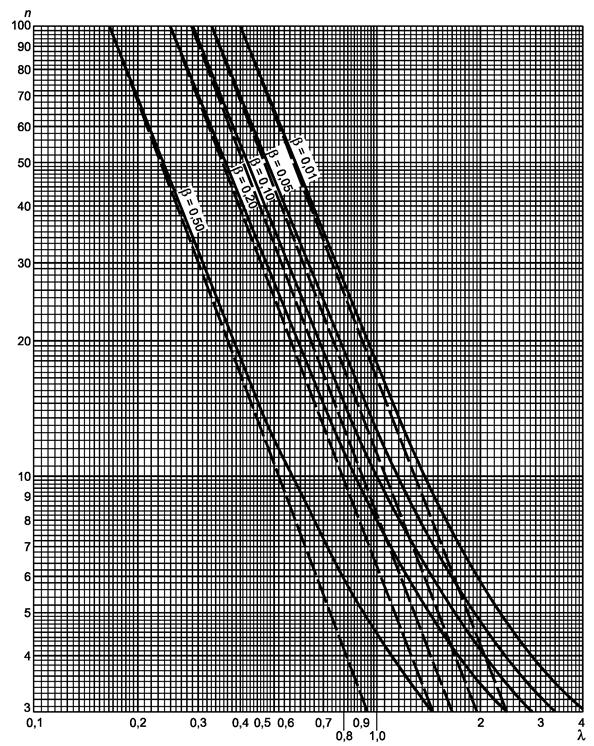
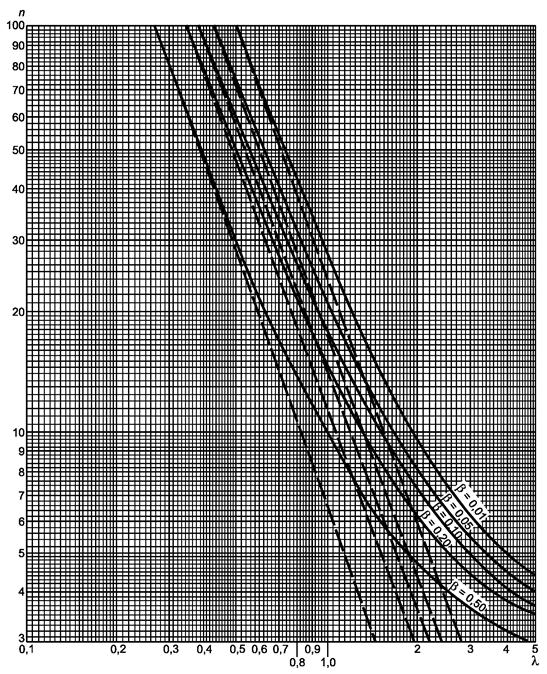
Рисунок 3.2. - Односторонний критерий сравнения средних (риск первого рода a = 0,05)
a) Гипотеза m £ m0 или m ³ m0:
-
если s
известно, используют прямые прерывистые линии с ![]()
-
если s
неизвестно, используют кривые с ![]()
b) Гипотеза m1 £ m2 или m1 ³ m2:
-
если s1 = s2 = s известно,
используют прямые прерывистые линии с ![]()
-
если s1 = s2 = s
неизвестно, используют кривые с ![]()
n1 = n2 = n (общий объем двух выборок).
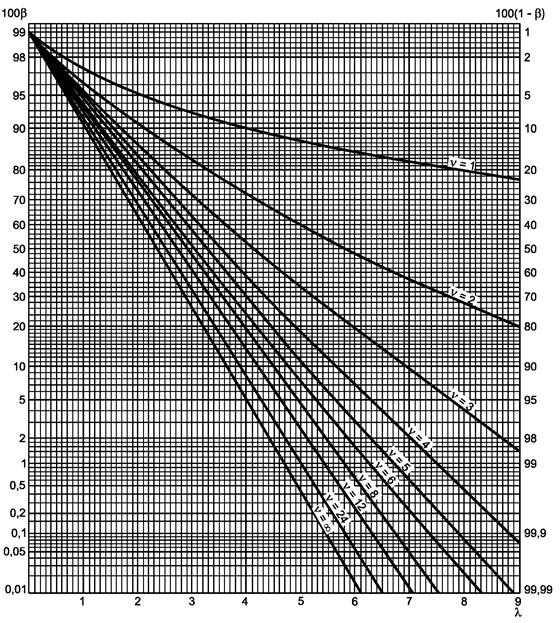
Рисунок 4.1 - Односторонний критерий сравнения средних (риск первого рода a = 0,01)
a) Гипотеза m £ m0 или m ³ m0:
-
если s
известно, используют кривую ν = ∞ с ![]()
-
если s
неизвестно, используют кривую ν = п - 1 с ![]()
b) Гипотеза m1 £ m2 или m1 ³ m2:
-
если s1 и s2
известны, используют кривую ν = ∞ с 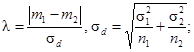
- если s1 и s2 неизвестны, используют кривую ν = n1 + n2 - 2
с 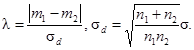
Рисунок 4.2 - Односторонний критерий сравнения средних (риск первого рода a = 0,01)
a) Гипотеза m £ m0 или m ³ m0:
-
если s
известно, используют прямые прерывистые линии с ![]()
-
если s
неизвестно, используют кривые с ![]()
b) Гипотеза m1 £ m2 или m1 ³ m2:
-
если s1 = s2 = s
известно, используют прямые прерывистые линии с ![]()
-
если s1 = s2 = s
неизвестно, используют кривые с ![]()
n = n2 = n (общий объем двух выборок).
Логарифмический масштаб для 0,1 < λ < 1
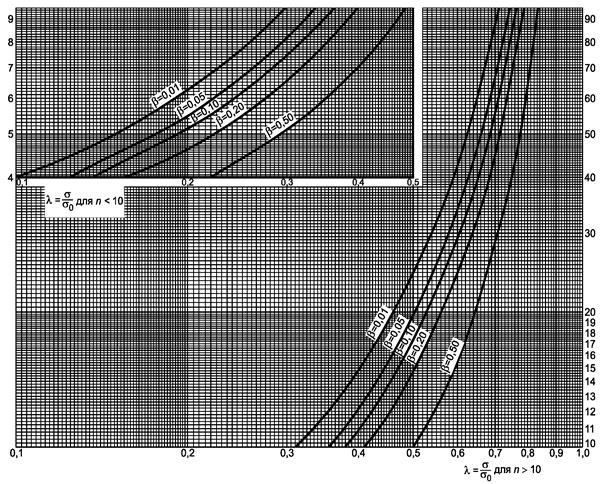
Рисунок 5.1 - Двусторонний критерий сравнения дисперсии с заданным значением (риск первого рода a = 0,05), лист 1
Гипотеза s2 = s02, λ = s/s0.
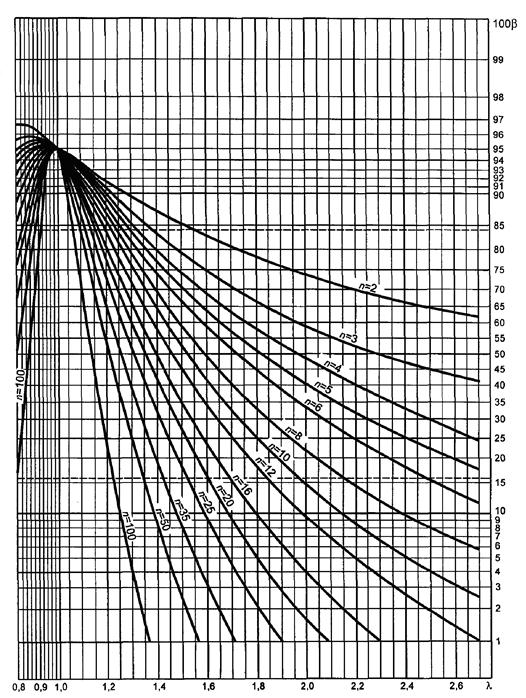
Линейный масштаб для λ > 1
Рисунок 5.1, лист 2
Гипотеза s2 = s02, λ = s/s0.
Рисунок 5.2 - Двусторонний критерий сравнения дисперсии с заданным значением (риск первого рода a = 0,05), лист 1
Гипотеза s2 = s02, λ = s/s0.
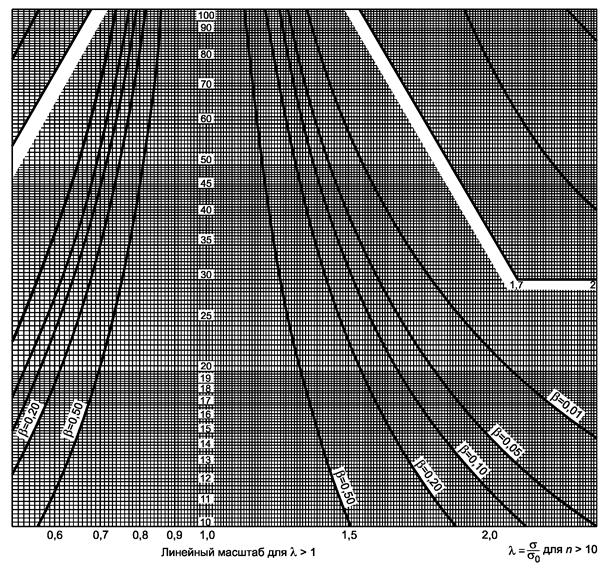
Рисунок 5.2, лист 2
Гипотеза s2 = s02, λ = s/s0.
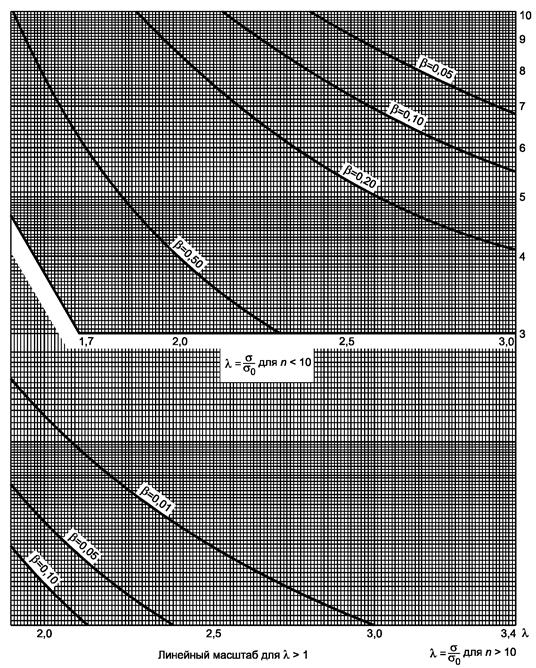
Рисунок 5.2, лист 3
Гипотеза s2 = s02, λ = s/s0.
Рисунок 6.1 - Двусторонний критерий сравнения дисперсии с заданным значением (риск первого рода a = 0,01), лист 1
Гипотеза s2 = s02, λ = s/s0.
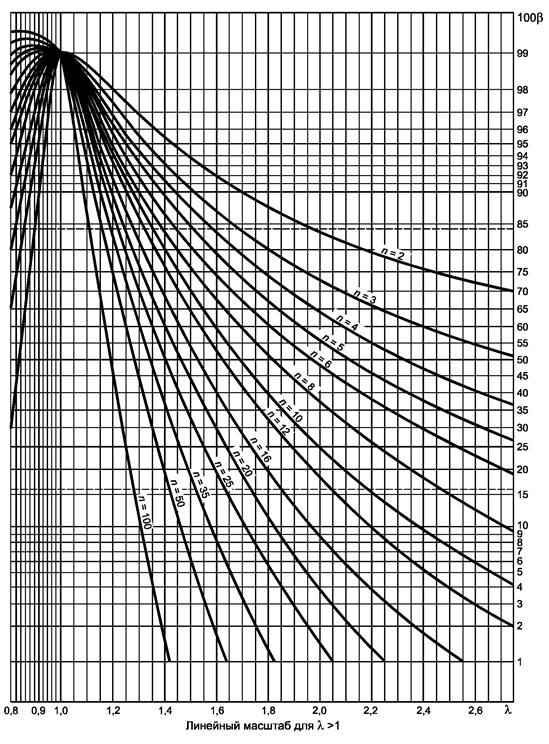
Рисунок 6.1, лист 2
Гипотеза s2 = s02, λ = s/s02.
Рисунок 6.2 - Двусторонний критерий сравнения дисперсии с заданным значением (риск первого рода a = 0,01), лист 1
Гипотеза s2 = s02, λ = s/s0.
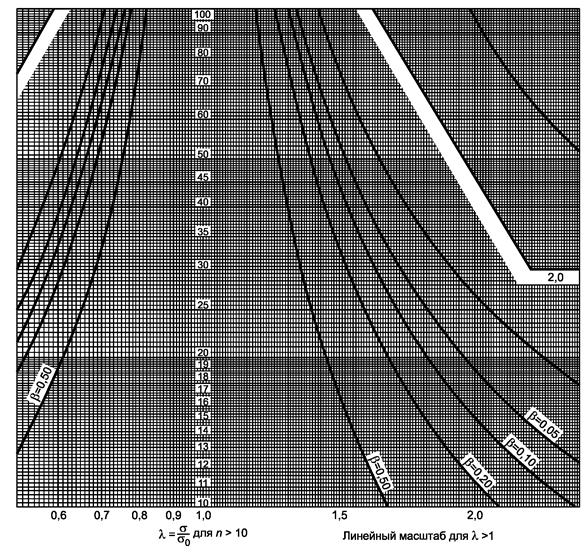
Рисунок 6.2, лист 2
Гипотеза s2 = s02, λ = s/s0.
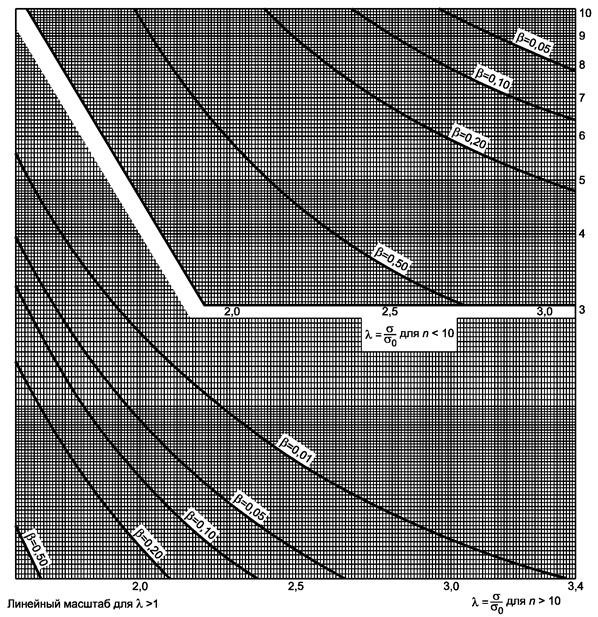
Рисунок 6.2, лист 3
Гипотеза s2 = s02, λ = s/s0.
Рисунок 7.1 - Односторонний критерий сравнения дисперсии с заданным значением (риск первого рода a = 0,05)
Гипотеза s2 £ s02, ![]()
Рисунок 7.2 - Односторонний критерий сравнения дисперсии с заданным значением (риск первого рода a = 0,05)
Гипотеза s2 £ s02, ![]()
Рисунок 8.1 - Односторонний критерий сравнения дисперсии с заданным значением (риск первого рода a = 0,01)
Гипотеза s2 £ s02, ![]()
Рисунок 8.2 - Односторонний критерий сравнения дисперсии с заданным значением (риск первого рода a = 0,01)
Гипотеза s2 £ s02, ![]()
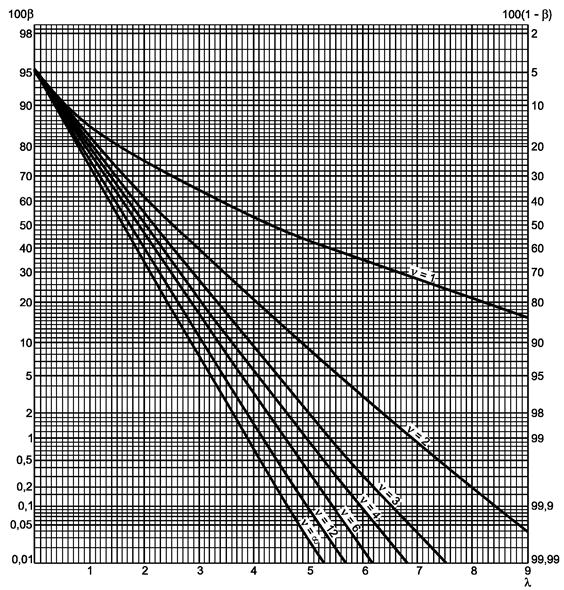
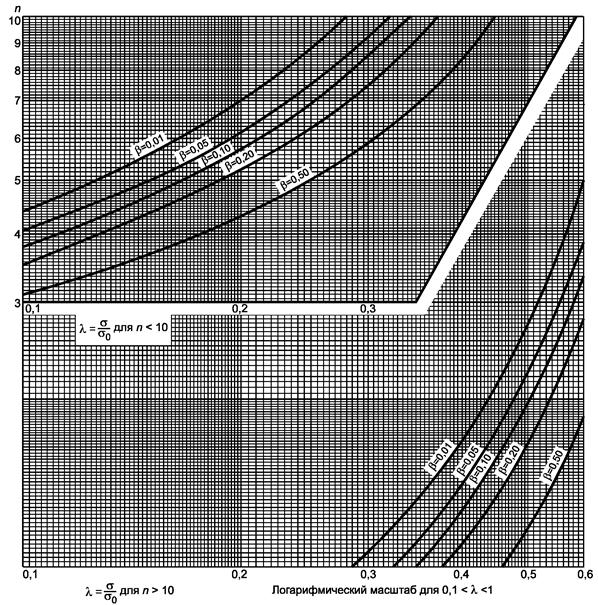
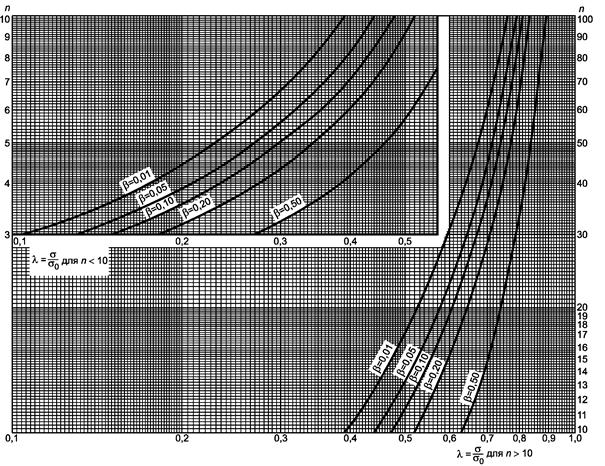
Рисунок 9.1 - Односторонний критерий сравнения дисперсии с заданным значением (риск первого рода a = 0,05)
Гипотеза s2 ³ s02, ![]()
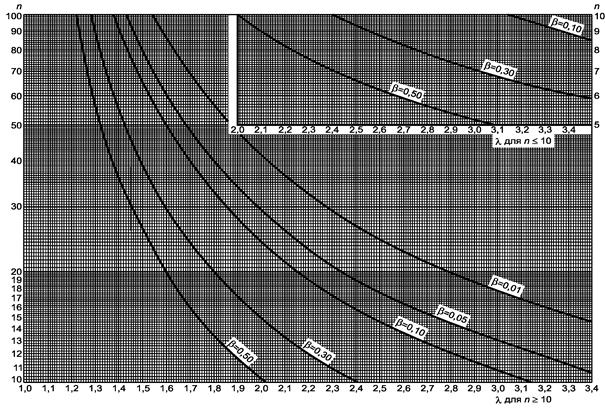
Рисунок 9.2 - Односторонний критерий сравнения дисперсии с заданным значением (риск первого рода a = 0,05)
Гипотеза s2 ³ s02, ![]()
Рисунок 10.1 - Односторонний критерий сравнения дисперсии с заданным значением (риск первого рода a = 0,01)
Гипотеза s2 ³ s02, ![]()
Рисунок 10.2 - Односторонний критерий сравнения дисперсии с заданным значением (риск первого рода a = 0,01)
Гипотеза s2 ³ s02, ![]()
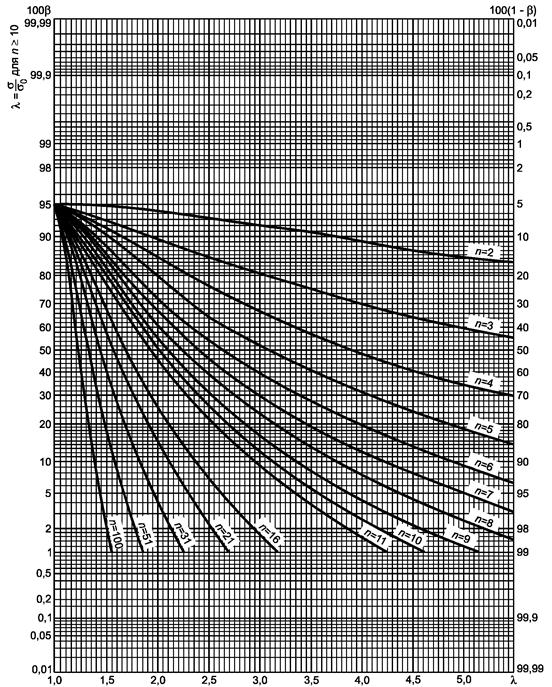
Рисунок 11.1 - Двусторонний критерий сравнения дисперсии с заданным значением (риск первого рода a = 0,05)
Гипотеза s12 = s22:
- для альтернативы s1 > s2, λ = s1/s2;
- для альтернативы s1 < s2, λ = s2/s1.
Рисунок 11.2 - Двусторонний критерий сравнения дисперсии с заданным значением (риск первого рода a = 0,05)
Гипотеза s12 = s22:
- для альтернативы s1 > s2, λ = s1/s2;
- для альтернативы s1 < s2, λ = s2/s1.
Рисунок 12.1 - Двусторонний критерий сравнения дисперсии с заданным значением (риск первого рода a = 0,01)
Гипотеза s12 = s22
- для альтернативы s1 > s2, λ = s1/s2;
- для альтернативы s1 < s2, λ = s2/s1.
Рисунок 12.2 - Двусторонний критерий сравнения дисперсии с заданным значением (риск первого рода a = 0,01)
Гипотеза s12 = s22:
- для альтернативы s1 > s2, λ = s1/s2;
- для альтернативы s1 < s2, λ = s2/s1.
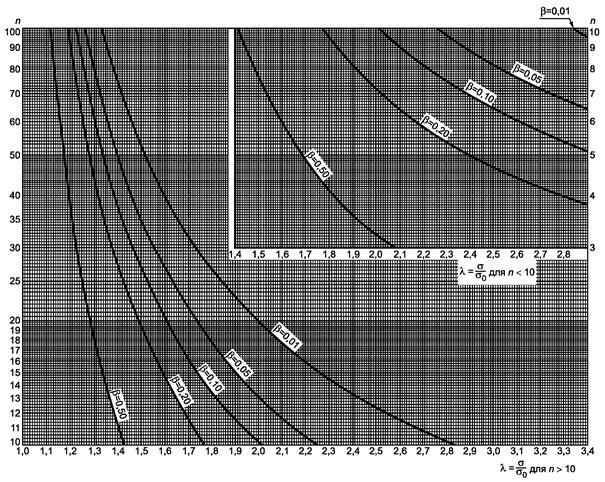
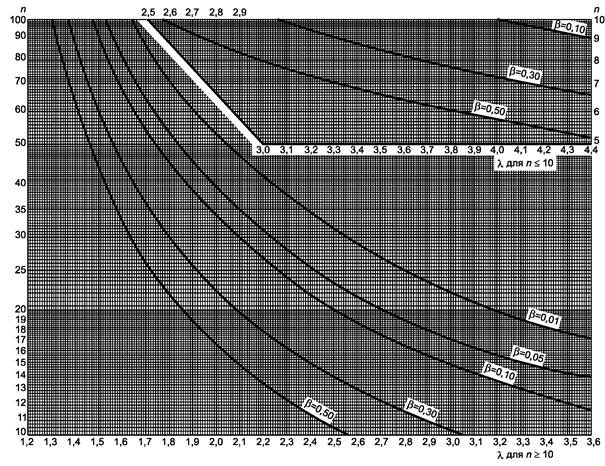
Рисунок 13.1 - Односторонний критерий сравнения дисперсии с заданным значением (риск первого рода a = 0,05)
a) Гипотеза s12 £ s22, λ = s1/s2.
b) Гипотеза s12 ³ s22, λ = s2/s1.
Рисунок 13.2 - Односторонний критерий сравнения дисперсии с заданным значением (риск первого рода a = 0,05)
a) Гипотеза s12 £ s22, λ = s1/s2.
b) Гипотеза s12 ³ s22, λ = s2/s1.
Рисунок 14.1 - Односторонний критерий сравнения дисперсии с заданным значением (риск первого рода a = 0,01)
a) Гипотеза s12 £ s22, λ = s1/s2.
b) Гипотеза s12 ³ s22, λ = s2/s1.
Рисунок 14.2 - Односторонний критерий сравнения дисперсии с заданным значением (риск первого рода a = 0,01)
a) Гипотеза s12 £ s22, λ = s1/s2.
b) Гипотеза s12 ³ s22, λ = s2/s1.
Приложение А
(справочное)
Сопоставление структуры настоящего стандарта со структурой примененного в нем международного стандарта ИСО 3494:1976
|
Структура международного стандарта ИСО 3494:1976 |
Структура настоящего стандарта |
||||
|
Часть 1 |
- |
||||
|
Раздел |
Подраздел |
Пункт |
Раздел |
Подраздел |
Пункт |
|
Общие замечания |
- |
- |
|||
|
1 |
1.1 |
- |
- |
||
|
1.2 |
- |
- |
|||
|
1.3 |
- |
- |
|||
|
1.4 |
- |
- |
|||
|
1.5 |
1.5.1 |
||||
|
1.5.2 |
|||||
|
2 |
2.1 |
- |
- |
||
|
2.2 |
- |
- |
|||
|
2.3 |
- |
- |
|||
|
2.4 |
- |
- |
|||
|
2.5 |
2.5.1 |
||||
|
2.5.2 |
|||||
|
3 |
3.1 |
- |
- |
||
|
3.2 |
- |
- |
|||
|
3.3 |
- |
- |
|||
|
3.4 |
- |
- |
|||
|
3.5 |
3.5.1 |
||||
|
3.5.2 |
|||||
|
4 |
4.1 |
- |
- |
||
|
4.2 |
- |
- |
|||
|
4.3 |
- |
- |
|||
|
4.4 |
- |
- |
|||
|
4.5 |
4.5.1 |
||||
|
4.5.2 |
|||||
|
5 |
5.1 |
- |
- |
||
|
5.2 |
- |
- |
|||
|
5.3 |
- |
- |
|||
|
5.4 |
- |
- |
|||
|
5.5 |
5.5.1 |
||||
|
5.5.2 |
|||||
|
6 |
6.1 |
- |
- |
||
|
6.2 |
- |
- |
|||
|
6.3 |
- |
- |
|||
|
6.4 |
- |
- |
|||
|
6.5 |
6.5.1 |
||||
|
6.5.2 |
|||||
|
Часть 2 |
|||||
|
- |
Раздел |
Подраздел |
Пункт |
||
|
- |
- |
- |
|||
Ключевые слова: проверка гипотез, случайная величина, функция распределения, выборка, среднее, дисперсия, стандартное отклонение, мощность критерия